计算机组成原理---关于乘法电路与除法运算电路的理解

一.乘法电路

1.无符号数乘法运算的硬件实现逻辑：

2.补码1位乘法运算的硬件实现逻辑：

3.无符号阵列乘法器

4.补码阵列乘法器

二.除法电路

1.原码除法运算

2.补码除法运算（不恢复余数法）

本篇是看湖科大与王道视频总结：

一.乘法电路

在手算乘法时，每进行一位乘法得到部分积（每次乘法后得到的乘积），都要错开一位：

所以位积向前一位错开的原因就是为了保证小数点的对齐：

迁移到计算机中二进制乘法的运算同理：

怎么将手算过程用计算机实现呢？需要解决两个问题：

1.运算过程中，会产生的多个位积，这些位积需要使用多个寄存器进行暂存，以便最后进行一次性相加。
2.乘积的数据宽度增长了一倍，这将造成硬件资源浪费和运算时间的增加。例如上面的例子输入的数据小数点后只有4位，而输出的数据增长为小数点后8位。

针对问题1：

拿以下乘式举例，经过整理可以发现，若乘数小数点后有n位，那么进行n次的先加法后移位就能得到最终的乘积。

这就是为什么我们做题时，需要用这样的方式：

注：这里虽然是原码的一位乘法，但是其符号的确定是通过将x，y异或得到的，所以前面的计算过程可以看作无符号数的计算。

这样，只需要

① 1个位宽为4位的寄存器存放被乘数x；

② 1个位宽为4位的寄存器存放部分积

③ 1个位宽为4位的寄存器最终乘积的高位和低位。

初始阶段高位寄存器被清0，低位寄存器存放乘数y。

针对问题2：

在运算器中，ALU用来实现乘法运算（加法和移位运算），ACC用来存放乘积高位，MQ用来存放乘数和乘积低位，X用来存放被乘数。这样，将乘积分为乘积低位和乘积高位分开存放，就不需要额外的位数存储乘积了。

1.无符号数乘法运算的硬件实现逻辑：

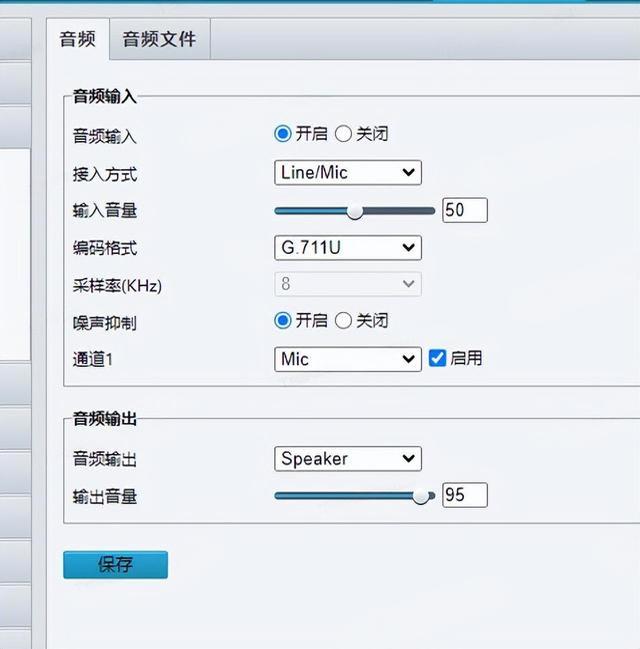
① 初始时，被乘数会被放到X寄存器中，乘数被放到MQ中，而ACC和Cout初始都为0，计数器Cn的值为4，因为乘数y的整数形式为4位：

② 由于MQ的最低位为1，所以ALU对ACC和X中的内容进行加法运算，并且在写使能的控制下将运算结果写入到ACC中：

控制逻辑会通过右移信号控制Cout，ACC，MQ同时向右移动一位。MQ中的内容同时向右移动一位，MQ中最低位的内容被移出，丢弃。Cout中的“1”，移动到ACC中的第1位，Cout补0即可。因为是无符号数的右移，所以进行逻辑右移即可。

注：分不清逻辑右移，算术右移等，可以看看：

http://t.csdnimg.cn/GChue

③ 至此，第一轮的先加法后移位就完成了，Cn变为3。表示还剩余3次加法和移位操作。

④ 以此类推，若MQ最后低位为0，那么只进行右移操作，右移后，最后一位丢弃即可。

⑤ 运算结束后，ACC中保存的就是乘积高位，MQ中保存的就是乘积低位。

结果为0.1000 1111

对照王道书中对这一部分的讲解：

这里的乘积寄存器P即ACC，乘积寄存器Y即MQ，Cn初值置32，是因为进行的是32位的无符号乘法运算。

这里的“每次从寄存器Y移出的最低位都被送到控制逻辑，以决定被乘数是否“加”到部分积上。”就是判断MQ的最低位是否为“1”。若为1，则进行加法运算再右移，若为0，则只进行右移。

经过上面的讲解，这一段理解就清楚了。

2.补码1位乘法运算的硬件实现逻辑：

相比于无符号数的运算逻辑，补码的乘法运算需要一位辅助位，辅助位是由MQ扩展出的一位存储。整体右移时，辅助位会被丢弃，而MQ中参与乘运算的最后一位会变为辅助位。

由于计算机中寄存器的位数都是统一的，由于MQ多增加了1位，所以ACC和X也相应增加1位。

补码1位乘法运算中，每次加法可能加+[+x]补，+[-x]补，+0，推导起来过程比较繁琐，如果想知道可以搜索“Booth”算法的推导和分析。具体情况如下（这里的MQ的最低位指的是参与运算的最低位）：Y4表示MQ的最低位，Y5表示辅助位。

有n位数值位，所以需要进行n位的加法和右移，最后还需要额外进行一次加法，这一次的加法加什么是和乘数的符号位有关的，所以说“补码乘数的符号位是参与运算的”。

与之前将的原码的乘法运算进行对比：

硬件实现逻辑如下：

相比于无符号数的硬件实现逻辑，增加了选择器，译码器和反相器：

Yi+1-Yi=0：

译码器对“辅助位-MQ中最低位”的值进行译码，若相减结果为0：输出译码结果（1有效信号，0无效信号），选择器选择输入端接收到有效信号后，会将输入端的“全0”从数据输出端输出，作为其中一个操作数。

Yi+1-Yi=1：

选择器会将x寄存器中的被乘数的补码输出到ALU中，作为其中一个操作数。

Yi+1-Yi=-1：

选择器会将寄存器x中的内容做取反操作，作为输出，同时需要进行+1操作，这样就可以为实现，由[x]补+[y]补---->[x]补+[-y]补

来看一下实现步骤：

① 初始时MQ存放乘数，X存放被乘数，辅助位初始位0，ACC初始为0，计数器Cn为0（不包括辅助位）

由于1-0等于1，所以做被乘数取反+1的操作。

② 将ALU中计算的结果会在写使能的控制下，将结果写入ACC。控制逻辑发送右移信号，使得ACC和MQ同步右移一位，由于是算术右移，所以ACC的最高位补符号位0。移出的最后一位丢弃即可。Cn更新为3，表示还剩余3次加法和算术右移操作。

③ Cn变为0后，还要额外再进行1次加法操作，由于1-0=1，所以进行取反+1的操作。最后更新到ACC中。

注意:MQ中的最低两位分别是乘数y的符号位和辅助位，需要舍弃，所以最后结果为：

0.0111 0101（单符号位的补码形式）

3.无符号阵列乘法器

原码、补码一位乘法的硬件逻辑实现，需要在时钟节拍下、通过控制逻辑的控制，执行相应轮次的“加法、右移”操作来实现，速度较慢。为了提高运算速度，可以仅采用组合逻辑电路以专用硬件方式构建阵列乘法器。

笔算乘法是这样的，

若采用组合逻辑电路实现：

如下图所示，某位的乘法运算可以采用与门实现，在进行加法运算时可以使用加法器进行运算，图中的“0”表示从低位的进位为0，而FA产生的进位，会用作下面一列的进位输入。

以此类推可以得到：

若被乘数x为1011，乘数y为1101，那么进行阵列乘法的过程如下：

以画圈部分举例，其是计算来自低位的两个进位，所以1+0=“1”，再加上同列中另一个加法器的运算结果“1”，得到本列的计算结果是“0”，并产生进位“1”。

性能分析：

与门的计算产生延迟1T，由于行间存在进位依赖，所以有3*6T；最后一行构成串行进位加法器，所以有时间延迟，（2*3+4）T。

注：关于串行加法器的时间延迟，可以看另一个视频：

3-2-5 定点数的加法和减法运算 — 串行进位加法器的硬件逻辑实现（无字幕版）_哔哩哔哩_bilibili

无符号阵列乘法器可以用于原码的乘法，因为原码的数值位可以看作无符号数，原码符号位单独处理（进行异或运算即可）。

4.补码阵列乘法器

补码阵列乘法器的思想：

如果将补码的符号位单独处理，将补码的数值位转换成原码的数值位，就可利用无符号阵列乘法器进行乘法运算。得到的结果为无符号乘积，将其转换成补码的数值位，然后在其前面添加单独处理的符号位即可得到补码乘法的结果。

Xf与Yf单独进行异或运算，同时Xf与Yf会决定求补电路的运算逻辑，例如，如果Xf为0，那么就不做变换，如果Xf为1，那么就需要数值位按位取反，末位+1

补充：对于求补电路，取反，末位+1的实现：

由上图可以看到需要n位加法器组成求补电路，硬件开销较大，可以用以下方式实现：

Xf=0时：

剩余位保持不变地输出：

Xf=1时：

依次类推，可以得到正确的结果：

来看一道真题：

答案如下：

补充3）问：a属于软件实现，b属于通用硬件实现，c属于专用硬件实现。

补充4）问：

二.除法电路

1.原码除法运算

除法运算中，ACC存放的是被除数，余数；通用寄存器X存放的是除数，MQ存放的是商。

注：原码除法运算中都是数值位去绝对值参加除法运算的，最后的符号位需要单独通过x和y异或得到，所以其实相当于无符号数的运算。所以中间采用的是逻辑移位。而补码运算中，由于符号位参与运算，所以采用的是算术移位。虽然都是低位补0，但是还是要说明一下。

在手算过程中，手算时每一位商取0/1是通过判断当前余数和除数的大小确定的，在计算机中，也就是要判断ACC中保存的内容和通用寄存器X中的内容谁更大，如果ACC内容（被除数）更大，商1，ACC内容小，商0。

1.不恢复余数法

① 计算机会先默认上商1，使得被除数-除数，即(ACC)+[-y]补，结果存放到ACC中。

② 若ACC中的结果为负数，即首位为1，那么说明被除数小于除数，应该商0才对。

所以计算机会恢复原来的ACC值，即(ACC)+[y]补。同时MQ最低位改为0。（如果ACC中结果为正，表示并没有上商错，不需要恢复）。

③ 整体逻辑左移，MQ低位补0，计算机依旧会默认先上商“1”，若结果为负再改为0。

④ 最后，ACC中存放的就是余数，MQ中存放的就是商。（如果最后一步商为负，需要恢复余数，并且上商改为0）商为0.1101，余数为0.0111*（2^-n），n为数值位位数。

⑤ 最后符号位单独运算，将x，y两个符号位进行异或运算即可。

现在来看这一段就非常容易理解，R表示的就是ACC，Q表示的就是MQ。

恢复余数法的手算过程如下：

2.不恢复余数法（加减交替法）

被除数-除数，若商为负，直接左移，再加[y]补。若商为正，处理方式和恢复余数法相同，即左移，然后+[-y]补。

整个过程加/减n+1次，每次加减确定一位商（余数为负商0，余数为正商1）；左移n次(最后一次加减完不移位)。最终可能还要再多一次加。