相信各位小伙伴都知道主成分分析的原理，我们今天用SPSS来实现一下主成分分析
主成分分析步骤
- 对原来的全部指标进行标准化，以消除变量在水平和量纲的影响
- 根据标准化的数据矩阵求出相关系数矩阵
- 求出协方差矩阵的特征根和特征向量
- 确定主成分，并对各个主成分的信息给出相关的解释
填充数据
首先，填充我们选择变量视图，接着填充下表所示的数据
点击数据视图，填入下表数据
现在我们把我们的数据准备好，要开始我们的数据处理了
指标标准化
点击上方的分析按钮，进入描述统计，再选择描述
把我们每一个指标都拖进另一个方框，并在左下角的将标准化值另存为变量进行勾选
我们就会得到这个页面
我们回到数据视图，可以看到这里把我们所勾选的指标进行标准化后的结果
用标准化数据矩阵求出相关系数矩阵
点击分析，再选择降维，进入因子（SPSS没有提供直接的主成分分析操作）
在这里把我们刚刚标准化后的数据选择进入变量这个位置
在描述这里，我们选择用初始解，相关性矩阵这里，我们选择KMO和巴特利特形度检验
在提取这里，我们选择如下（协方差和相关性任选一个即可）
旋转这个项目，我们选择无（旋转这一项操作是属于因子分析的，而我们这里要做的是主成分分析）
得分这里，我们要将其保存为变量（这里要勾选一下，
选项不进行理会，按下确定键
我们可以拿到这样的一个结果
成分矩阵
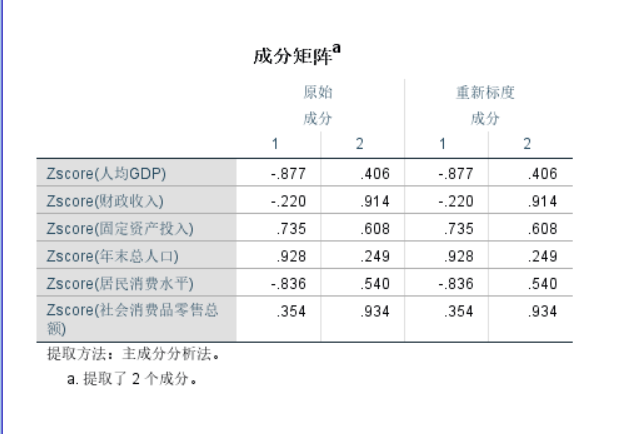
这些数据，我们应该怎么看呢，接下来，我们一个一个数据来分析
公因子分析
这里的公因子方差，我们不需要理会（做因子分析的时候要看这一项数据）
总方差解释
总方差解释中方差大小表示了信息量的多与寡，SPSS中当累计的方差百分比超过百分之八十五的时候，就会将这一项指标进行提取。这里的总计是指这项数据的大小，比例是指该项的总计占所有指标（这里有六项指标）的比例。根据这个规则，我们可以看到SPSS在这里选择前两项数据进行提取（前两项数据加起来已经达到了百分之九十三），注意下标：这里使用的是主成分分析法。
这里左下角有一行小字，提取了两个成分，这两个成分正是我们刚刚在方差解释中所提取的两项指标，现在我们来看看成分矩阵，原始数据我们就不看了，我们主要关注的是重新标度即对原始成分进行标准化后的成分。我们可以看到第一个提取到的成分在人均GDP,财政收入，居民消费水平中是为负的，说明第一项提取出来的指标和这几项成分呈负相关，而剩下的成分刚好相反。根据我们的高中知识就可以知道，当这个值的正负值越接近一的时候，这就说明相关性越高。我们留意到第一项指标在人均GDP，固定资产投资，居民消费水平，年末总人口。那么就说明第一项提取出来的成分主要是跟人均GDP，固定资产投资，居民消费水平，年末总人口的相关性较大，也就是代表了这几项数据，那么同理，第二项提取的指标主要是代表了财政收入，固定资产投资，社会消费品零售总额。
我们还可以通过看图来确定主成分
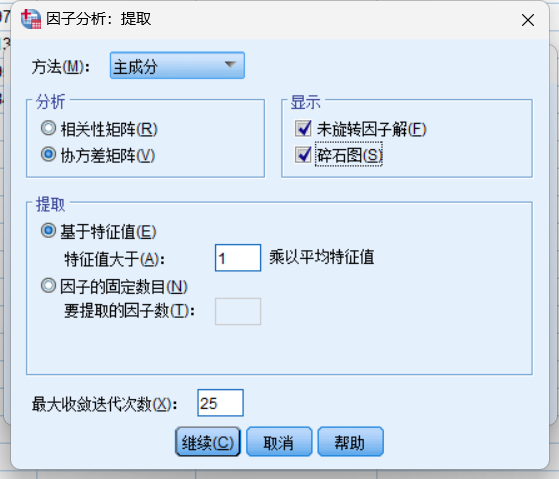
在这个页面内选择碎石图
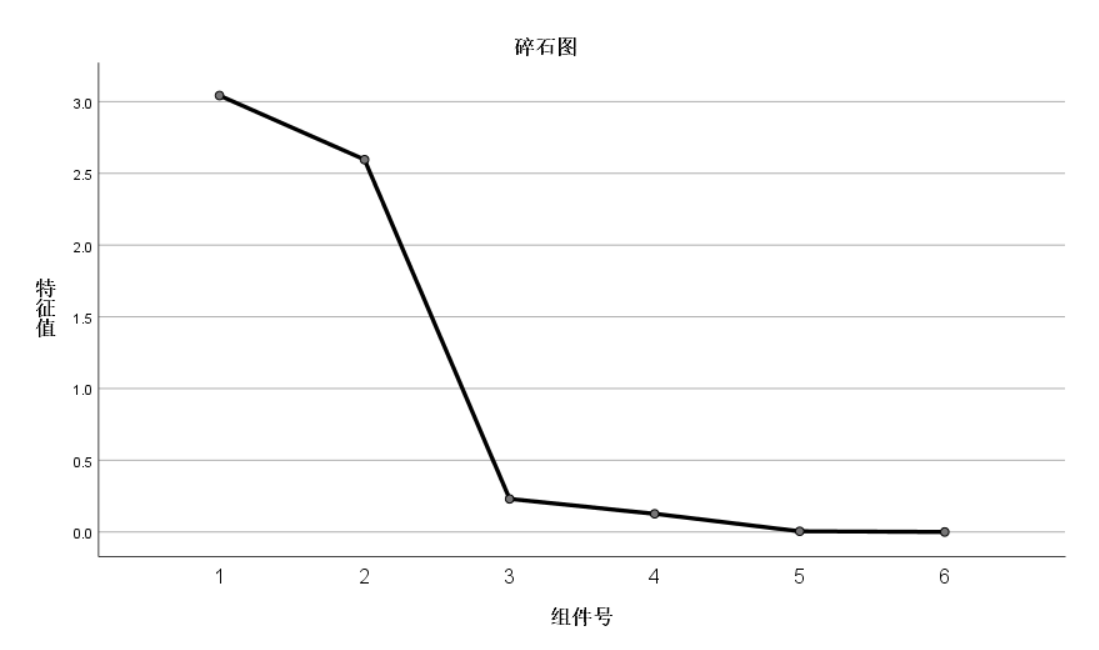
在斜率最大点的拐点前面的指标就是我们作为主成分的组件了
如果我们在这一张含有这么多数据的图中不好辨认的话，我们可以去画张图（能更直观地反应出变化以及帮我们去确认成分）
可以在分析中的因子分析->旋转中勾选载荷图
我们在结构那里可以得到这样一张图
越靠近上下两侧就说明和组件二的相关性越高，越靠近左右两侧的就说明和组件一的相关性越高。
转换成主成分分析
有同学会问这个前面的值是直接相乘的吗，我们在SPSS里面做的都是因子分析，而不是主成分分析，因为SPSS里面没有因子分析，我们想要做就要绕路
根据上面的这一幅图，我们发现了主成分分析的主要数据和因子分析法的主要数据的关系如上图右下方所示。根据这一个关系，我们进行转换。
我们把重新标度成分的数据拿过去进行转换（我们在视图变量这个页面里面把我们复制到的值改名为V1和V2）
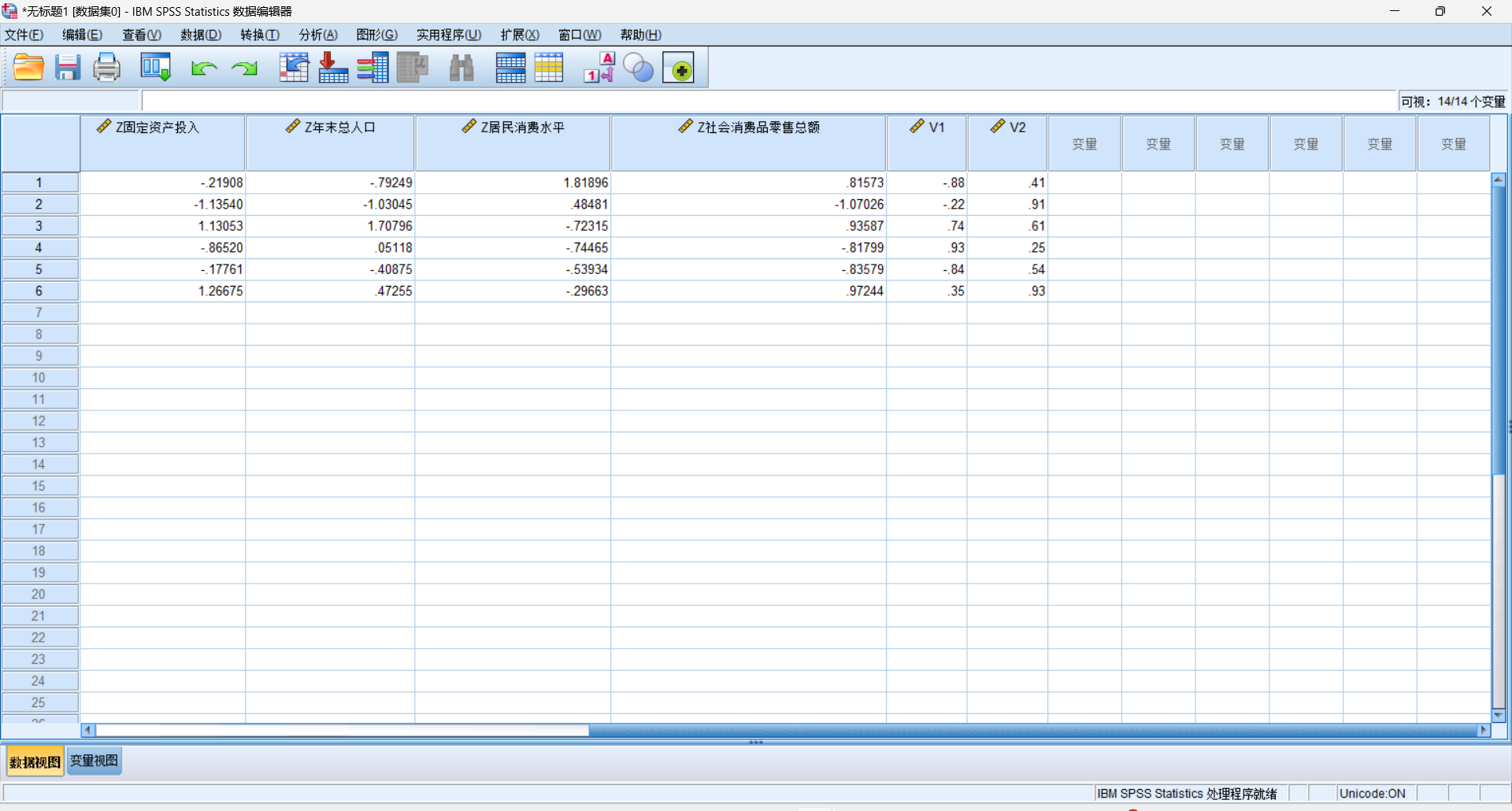
这里的3.042是我们刚刚在总方差解释对应的值。
这里的W1就是我们去做主成分分析的数据了（从因子分析转换过来的）
同理我们把我们的第二个数据也转换一下，命名为W2,运算式为V2/SQR(2.596)
计算最终值
我们采用W1中的第一个值乘上我们的第一个变脸，第二个值乘上第二个变量，以此类推，我们可以得到我们最终想要的数值。
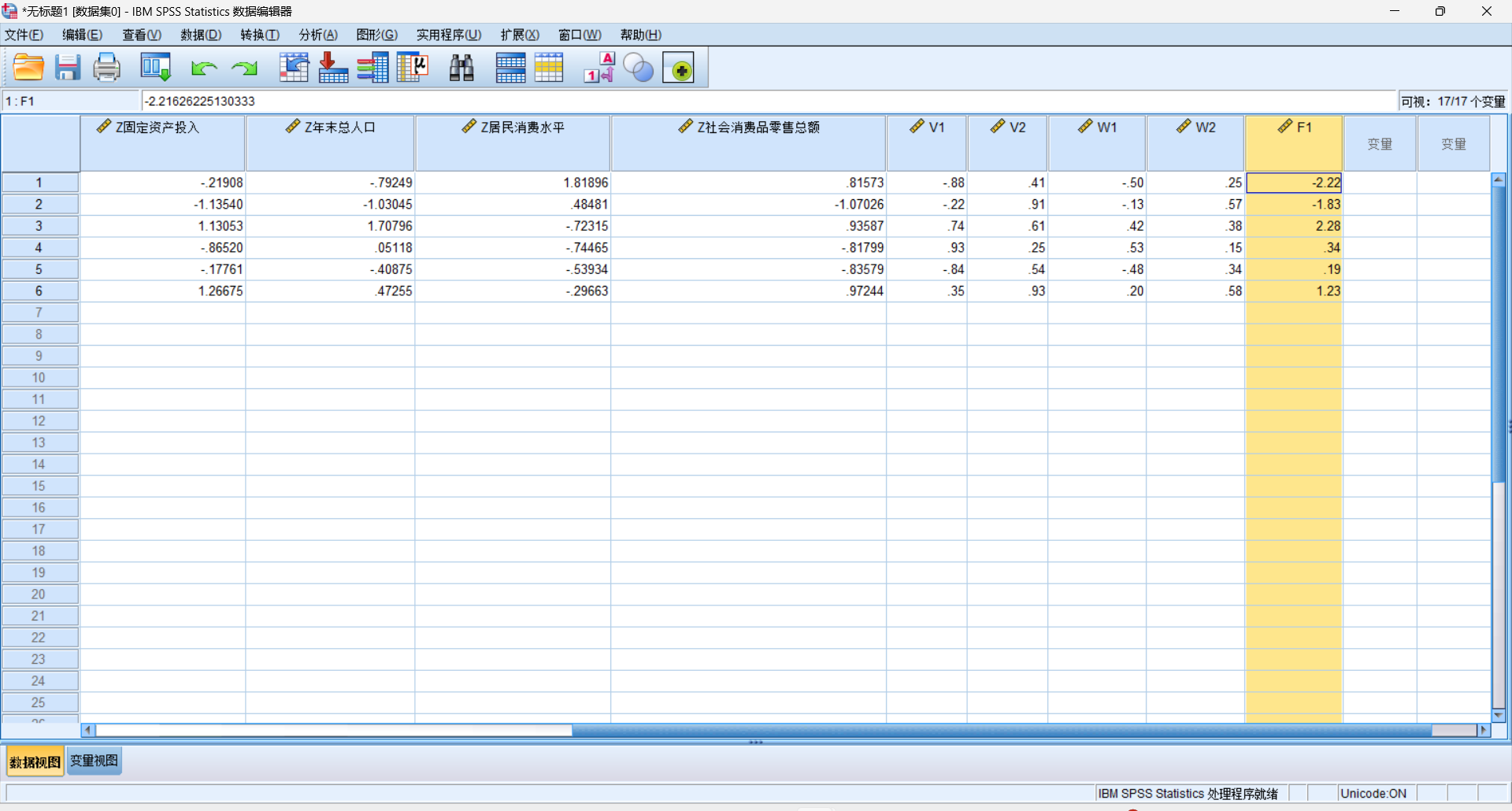
我们这里用F1这个指标就代替了先前那么多的指标，这就起到了一个降维的作用了（F2就同理）
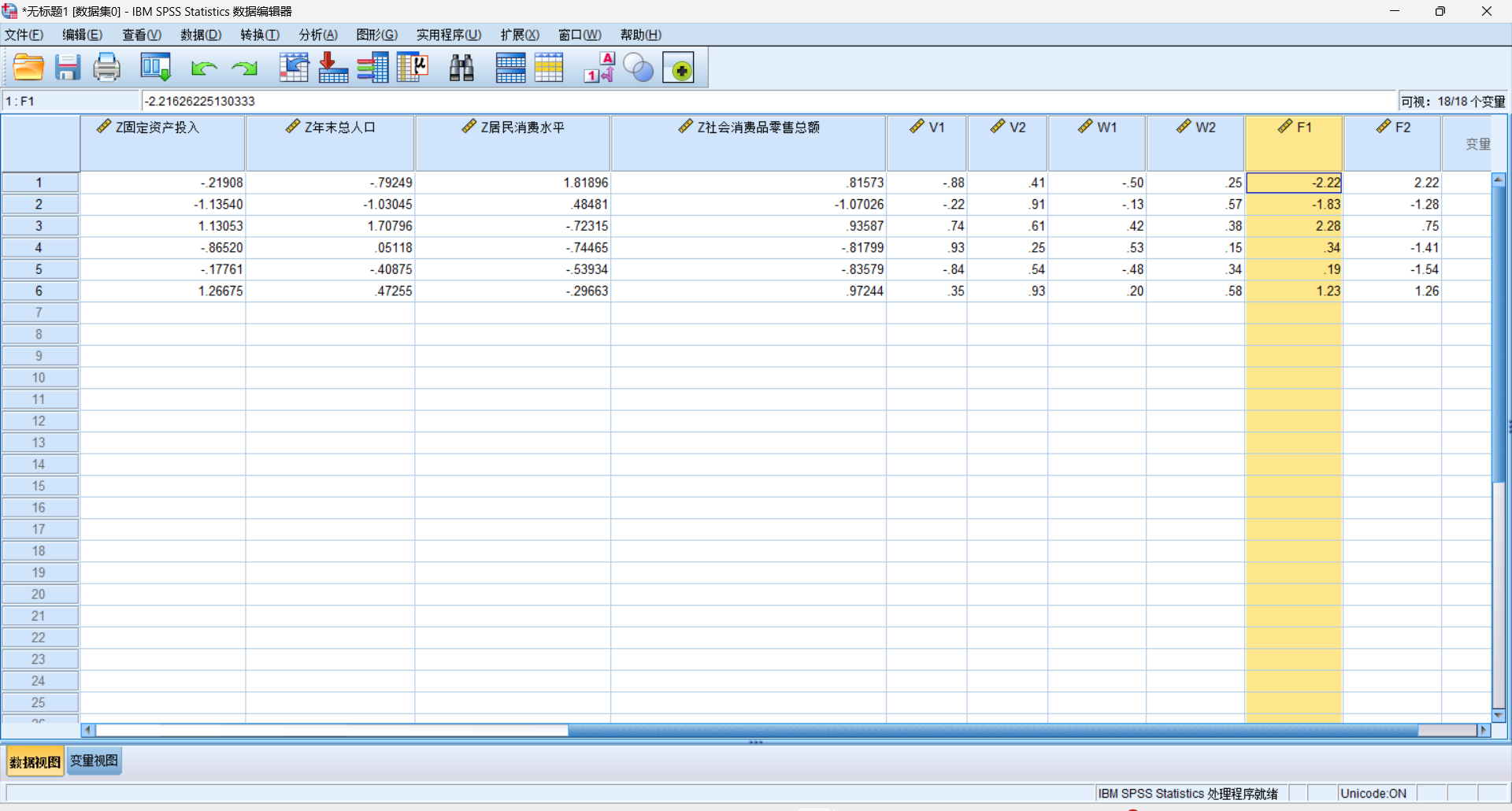拿到F1和F2这两组数据，我们就已经完成了对我们数据的降维。
