🥳🥳🥳 茫茫人海千千万万，感谢这一刻你看到了我的文章，感谢观赏，大家好呀，我是最爱吃鱼罐头，大家可以叫鱼罐头呦~🥳🥳🥳

如果你觉得这个【重启人生计划】对你也有一定的帮助，加入本专栏，开启新的训练计划，漫长成长路，千锤百炼，终飞升巅峰！无水文，不废话，唯有日以继日，终踏顶峰！ ✨✨欢迎订阅本专栏✨✨

❤️❤️❤️ 最后，希望我的这篇文章能对你的有所帮助！ 愿自己还有你在未来的日子，保持学习，保持进步，保持热爱，奔赴山海！ ❤️❤️❤️

🔥【重启人生计划】第零章序·大梦初醒🔥

🔥【重启人生计划】第壹章序·明确目标🔥

序言

大家好，我是最爱吃鱼罐头，距离离职已经过去一个月了，目前进度为1，打算重新找工作倒计时29天，当然这其中也会去投递面试。

生如夏花之绚烂，死如秋叶之静美。——泰戈尔《生如夏花》

今日回顾

今天开始，是真正进入计划的第一天，挑战之旅💪🏻，今日启程🔥。今天早上背诵jvm两天的内容，主要一天五道题的量有点少，后面会给自己慢慢提高难度，增加题量，接着10点多开始弄算法题，到11点半。今日算法题也是刷了两天的量，比较第一天实在有点少，我没额外去看视频提升，想着后面到难点时再冲。

算法回顾

两数之和

两数之和 📍

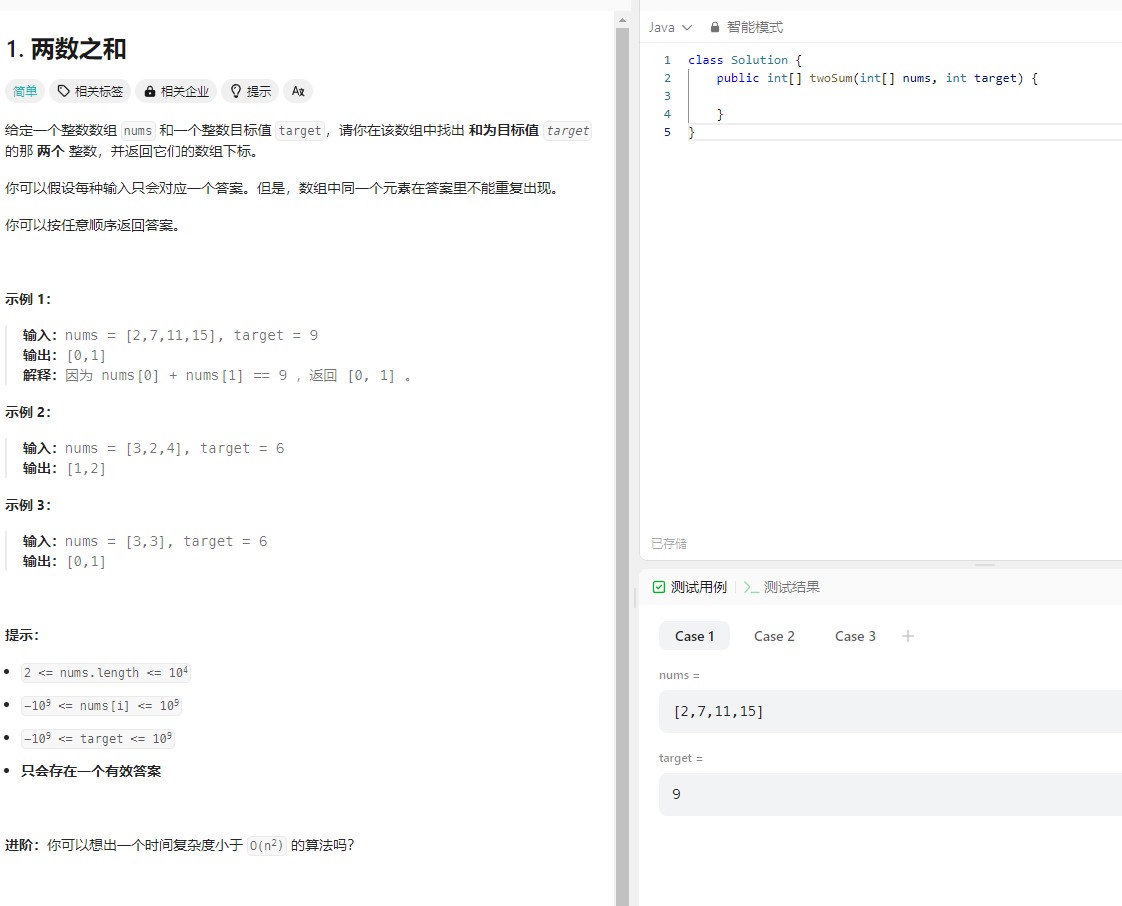
对于这道题的讲解呢，有两种比较简单的实现方式：

• 暴力破解法：要在数组中找到两个数相加为target值，直接两层for循环就可以搞定；
• 哈希表：也可以使用哈希表，通过一层for循环，不断判断哈希表是否有满足条件的值（即target - 当前的值 是否有存在在哈希表上），有直接返回。

代码实现：

package com.ygt.day1;

import java.util.HashMap;

/**
 * 1. 两数之和
 * https://leetcode.cn/problems/two-sum/description/
 * 给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。
 * 你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
 * 你可以按任意顺序返回答案。
 * 输入：nums = [2,7,11,15], target = 9
 * 输出：[0,1]
 * 解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
 *
 * @author ygt
 * @since 2024/8/12
 */
public class TwoSum {
    public static void main(String[] args) {
        int[] nums = {2,7,11,15};
        System.out.println("两数之和的答案：" + new TwoSum().twoSum(nums, 9));
    }

    /*方式1：暴力破解法*/
    public int[] twoSum(int[] nums, int target) {
        // 直接双层for循环遍历判断即可
        int[] result = new int[2];

        // 先判断下
        if(nums == null || nums.length < 2) {
            return result;
        }

        for (int i = 0; i < nums.length - 1; i++) {
            int first = nums[i];
            // 与后面一个逐一比较判断
            for (int j = i + 1; j < nums.length; j++) {
                int second = nums[j];
                // 如果相等就可以设置数组并退出循环
                if(first + second ==  target) {
                    result[0] = i;
                    result[1] = j;
                    break;
                }
            }
        }

        return result;
    }
    /*方式2：使用哈希表*/
    public int[] twoSum2(int[] nums, int target) {
        // 通过一层for循环，不断判断哈希表是否有满足条件的值，有直接返回
        HashMap<Integer, Integer> map = new HashMap<>();

        for (int i = 0; i < nums.length; i++) {

            // 判断 target减去当前的值后，哈希表是否有值存在
            if(map.containsKey(target - nums[i])) {
                return new int[]{map.get(target - nums[i]), i};
            }
            map.put(nums[i], i);
        }
        return new int[0];
    }
}

罗马数字转整数

罗马数字转整数 📍

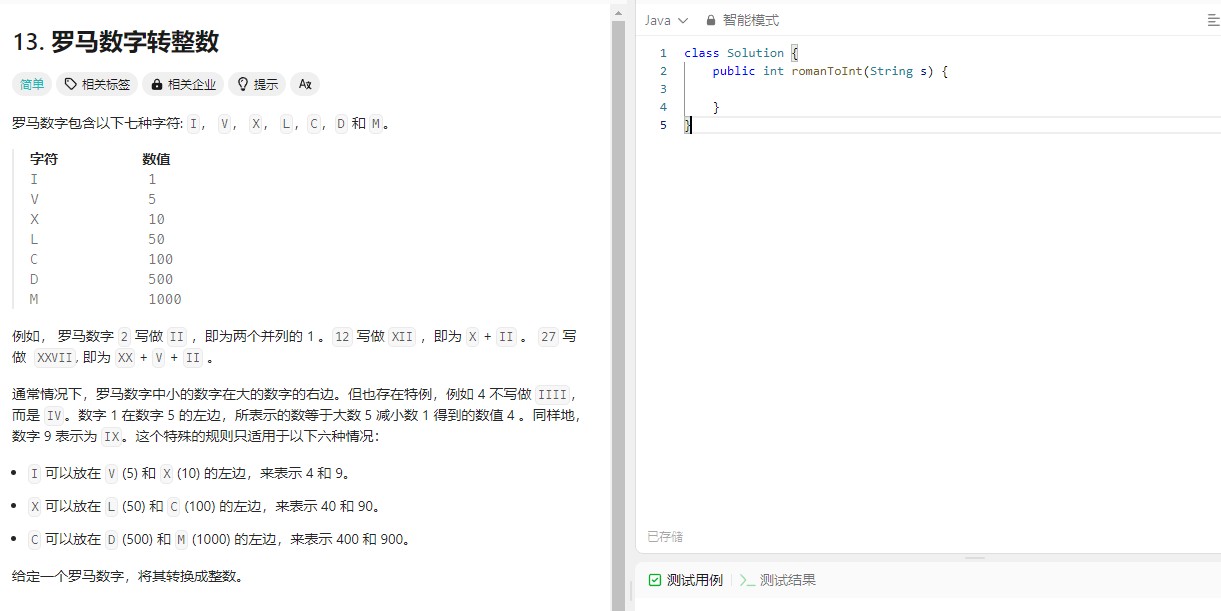
对于这道题的讲解呢，可以使用比较简单方式，使用哈希表存储有关罗马字符对应的数值，接着从字符串中不断拆分字符，从哈希表中得到对应的值进行累加。需要注意的点有特殊规则。

代码实现：

package com.ygt.day1;

import java.util.HashMap;

/**
 * 13. 罗马数字转整数
 * https://leetcode.cn/problems/roman-to-integer/description/
 * 罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。
 * 字符          数值
 * I             1
 * V             5
 * X             10
 * L             50
 * C             100
 * D             500
 * M             1000
 * 例如， 罗马数字 2 写做 II ，即为两个并列的 1 。12 写做 XII ，即为 X + II 。 27 写做  XXVII, 即为 XX + V + II 。
 * 通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，
 * 所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：
 * I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
 * X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
 * C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
 * 给定一个罗马数字，将其转换成整数。
 * 输入: s = "MCMXCIV"
 * 输出: 1994
 * 解释: M = 1000, CM = 900, XC = 90, IV = 4.
 * @author ygt
 * @since 2024/8/12
 */
public class RomanToInt {
    public static void main(String[] args) {
        String s = "MCMXCIV";
        System.out.println("罗马数字转整数的答案：" + new RomanToInt().romanToInt(s));
    }

    /*方式：直接将可能的结构存储在哈希表中，最后不断取出判断*/
    public int romanToInt(String s) {
        HashMap<Character, Integer> map = new HashMap<>(8);
        map.put('I', 1);
        map.put('V', 5);
        map.put('X', 10);
        map.put('L', 50);
        map.put('C', 100);
        map.put('D', 500);
        map.put('M', 1000);

        int result = 0;
        int length = s.length();

        // 需要额外注意：C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。
        // 就是可以理解为：前面一个数比后面的小的话，代表要减了，否则就加
        // 单独一个M为1000，而CM为900
        for (int i = 0; i < length; i++) {
            // 取出第一个值
            int value = map.get(s.charAt(i));

            // 当前字符串的索引边界判断 以及与后一个进行比较
            if(i < length - 1 && value < map.get(s.charAt(i + 1))){
                result -= value;
            }else {
                result += value;
            }
        }
        return result;
    }
}

二分查找

接着下面都是基于二分查找的模板去实现的。二分查找关键点在于是有序。

二分查找📍

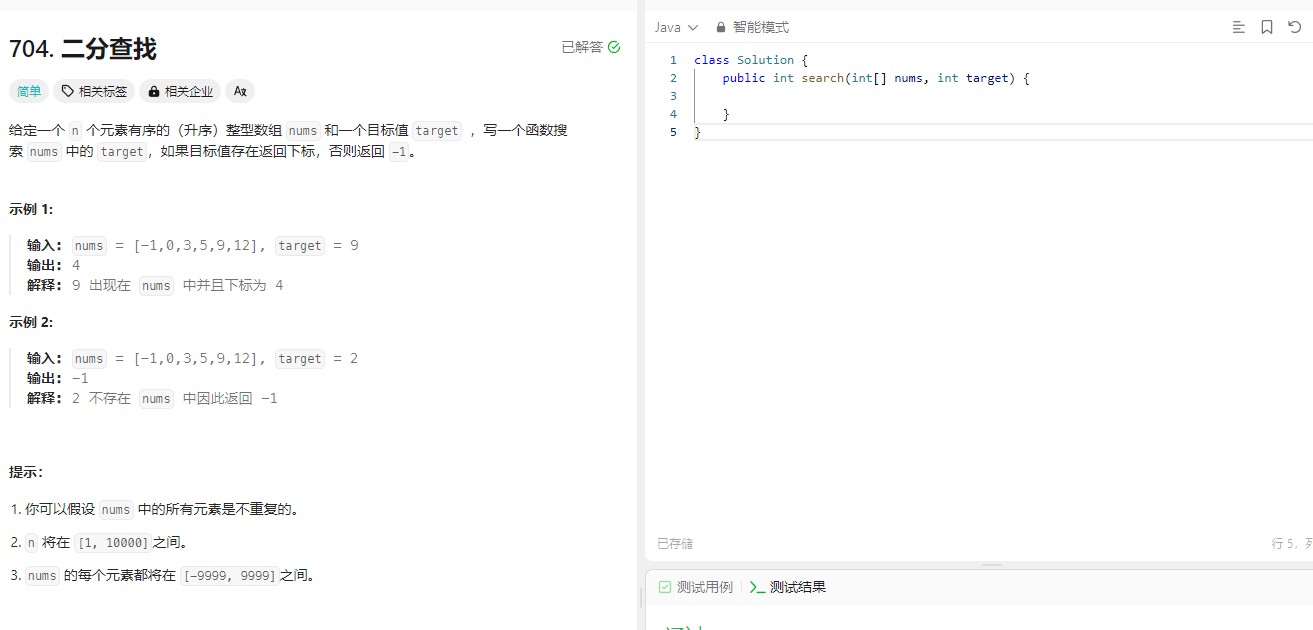
二分查找在数组上的应用是非常广泛的，简单概念可以理解下：

二分查找（Binary Search）是一种高效的查找算法，适用于在已排序的数据结构中查找特定的元素。它的基本思想是通过不断将搜索范围缩小一半来找到目标值。下面是二分查找的基本步骤：

1. 初始化：确定搜索范围的起始位置和结束位置，通常是数组的两个端点。
2. 计算中间位置：计算当前搜索范围的中间位置，即 mid = (low + high) / 2，其中 low 是当前搜索范围的起始位置，high 是结束位置。
3. 比较：
   • 如果中间位置的元素等于目标值，返回这个位置。
   • 如果中间位置的元素小于目标值，则目标值只能在中间位置的右边部分继续搜索（更新 low 为 mid + 1）。
   • 如果中间位置的元素大于目标值，则目标值只能在中间位置的左边部分继续搜索（更新 high 为 mid - 1）。
4. 重复：重复步骤2和步骤3，直到找到目标值或搜索范围为空（low 大于 high）。
5. 结束：如果搜索范围为空且未找到目标值，则目标值不在数组中。

也可以通过看视频来加深理解。

代码实现：

package com.ygt.day2;

/**
 * 704. 二分查找
 * https://leetcode.cn/problems/binary-search/description/
 * 给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
 * 输入: nums = [-1,0,3,5,9,12], target = 9
 * 输出: 4
 * 解释: 9 出现在 nums 中并且下标为 4
 * @author ygt
 * @since 2024/8/12
 */
public class Search {
    public static void main(String[] args) {
        int[] nums = {-1,0,3,5,9,12};
        System.out.println("二分查找的答案：" + new Search().search(nums, 9));
    }

    /*方式：从数组中间对半分，中间值与目标值比较，小了就往左，大了往右*/
    public int search(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = (left + right) / 2;
            if(nums[mid] > target) {
                right = mid - 1;
            }else if(nums[mid] < target) {
                left = mid + 1;
            }else {
                return mid;
            }
        }

        return -1;
    }
}

搜索插入位置

搜索插入位置📍

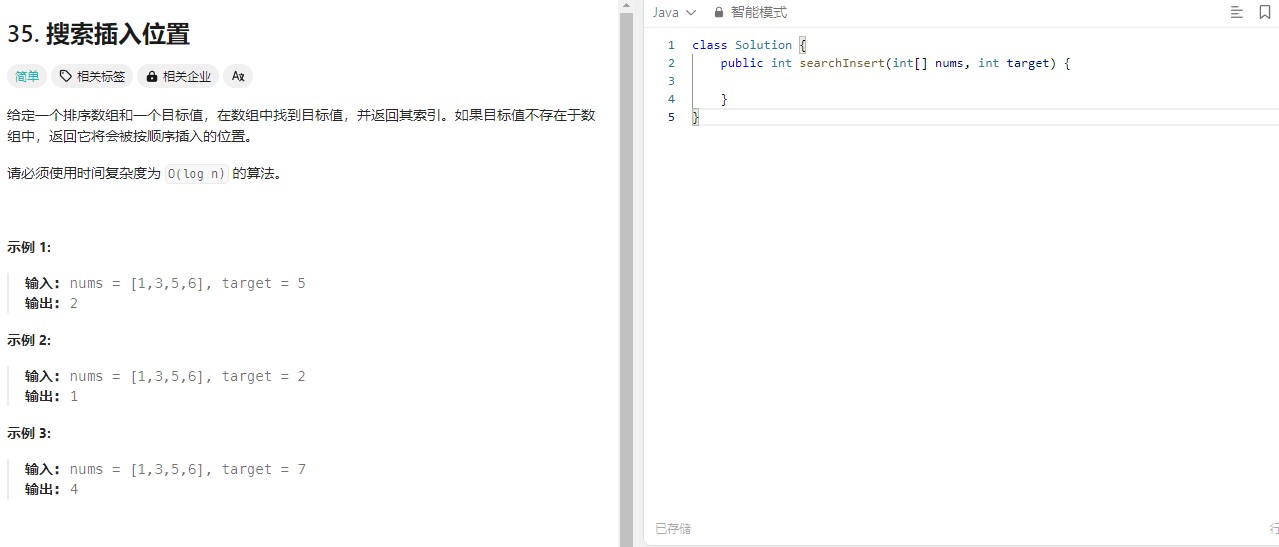
对于这道题的讲解呢，这道题基本就是基于二分查找的模板实现的，而与二分查找的区别，无非就是题目中，所说，如果目标值不存在于数组中，返回它将会被按顺序插入的位置，即已经在末尾或者开始处。

代码实现：

package com.ygt.day2;
/**
 * 35. 搜索插入位置
 * https://leetcode.cn/problems/search-insert-position/description/
 * 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。
 * 如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
 * 请必须使用时间复杂度为 O(log n) 的算法。
 * 输入: nums = [1,3,5,6], target = 5
 * 输出: 2
 * @author ygt
 * @since 2024/8/12
 */
public class SearchInsert {
    public static void main(String[] args) {
        int[] nums = {1,3,5,6};
        System.out.println("搜索插入位置的答案：" + new SearchInsert().searchInsert(nums, 5));
    }

    /*方式：从数组中间对半分，中间值与目标值比较，小了就往左，大了往右*/
    public int searchInsert(int[] nums, int target) {
        int left = 0;
        int right = nums.length - 1;

        while (left <= right) {
            int mid = (left + right) / 2;
            if(nums[mid] > target) {
                right = mid - 1;
            }else if(nums[mid] < target) {
                left = mid + 1;
            }else {
                return mid;
            }
        }

        // 与二分查找的区别，无非就是题目中，所说，如果目标值不存在于数组中，返回它将会被按顺序插入的位置，即已经在末尾或者开始处。
        return left;
    }
}

x 的平方根

x 的平方根📍

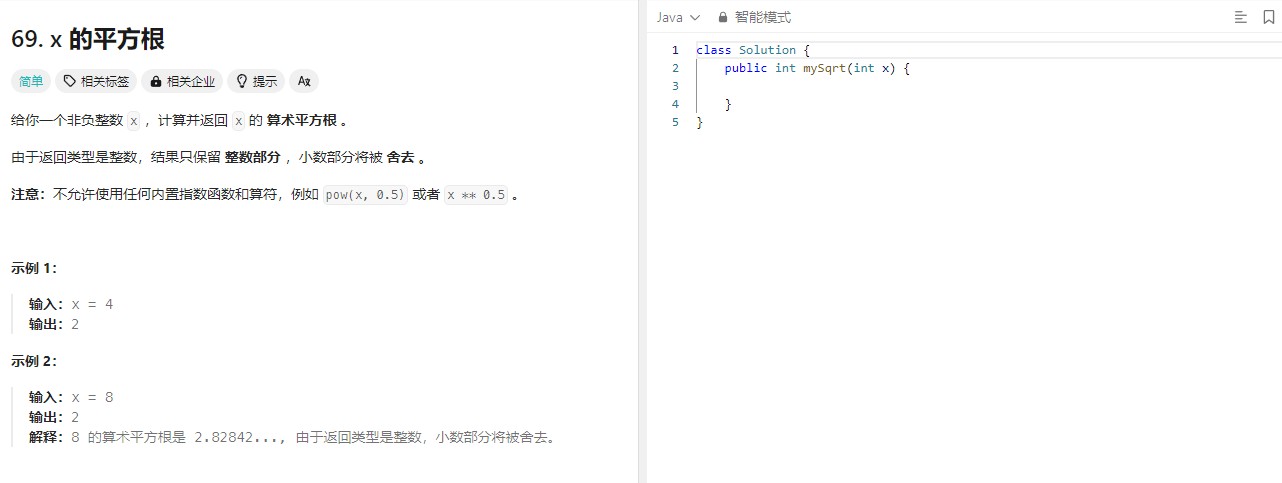
对于这道题的讲解呢，这道题基本就是基于二分查找的模板实现的，没啥好说的了。核心思想就是从0开始到目标值，取中间值的平方判断与x的大小，然后不断缩小上下界的范围。

代码实现：

package com.ygt.day2;

/**
 * 69. x 的平方根
 * https://leetcode.cn/problems/sqrtx/description/
 * 给你一个非负整数 x ，计算并返回 x 的 算术平方根 。
 * 由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。
 * 注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。
 * 输入：x = 4
 * 输出：2
 * @author ygt
 * @since 2024/8/12
 */
public class MySqrt {
    public static void main(String[] args) {
        int x = 8;
        System.out.println("x 的平方根的答案：" + new MySqrt().mySqrt(x));
    }

    /*方式：从数组中间对半分，中间值与目标值比较，小了就往左，大了往右*/
    public int mySqrt(int x) {
        // 从0开始，到目标值x处
        int left = 0, right = x, result = -1;

        // 思路:判断中间值的平方与x的大小，然后不断缩小上下界的范围。
        while(left <= right) {
            // 注意：为了避免乘法溢出
            int mid = (right - left) / 2 + left;

            // 是否比x小，只要找到第一个比x小的，代表找到了。
            if((long)mid * mid <= x) {
                result = mid;
                left = mid+1;
            }else {
                right = mid - 1;
            }
        }
        return result;
    }
}

有效的完全平方数

有效的完全平方数📍

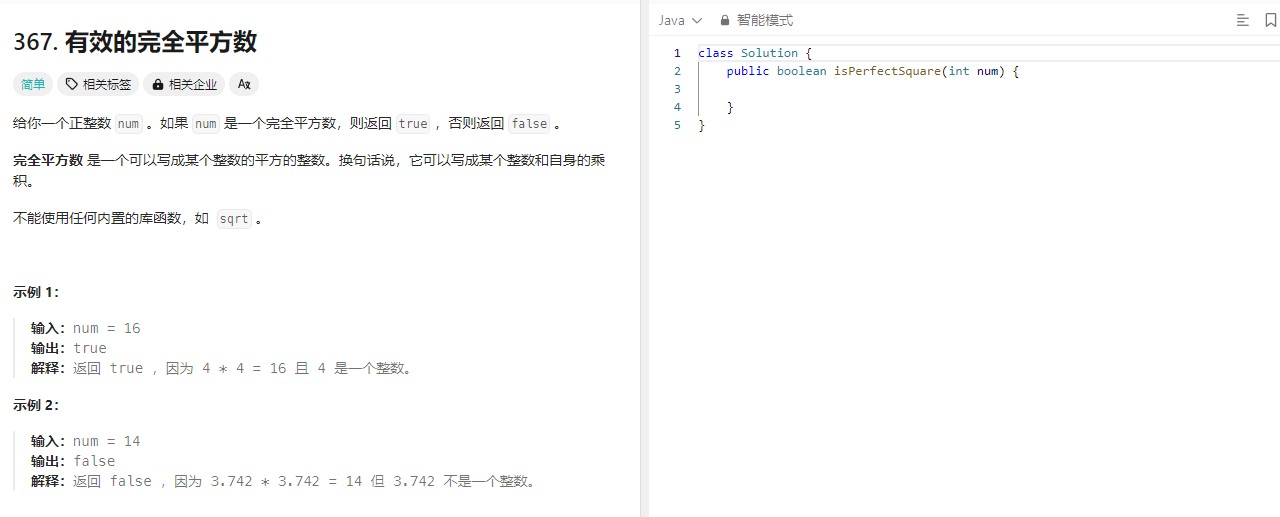
对于这道题的讲解呢，这道题基本就是基于二分查找的模板实现的，没啥好说的了。核心思想就是从0开始到目标值，取中间值的平方判断与x的大小，然后不断缩小上下界的范围。

代码实现：

package com.ygt.day2;

/**
 * 367. 有效的完全平方数
 * https://leetcode.cn/problems/valid-perfect-square/description/
 * 给你一个正整数 num 。如果 num 是一个完全平方数，则返回 true ，否则返回 false 。
 * 完全平方数 是一个可以写成某个整数的平方的整数。换句话说，它可以写成某个整数和自身的乘积。
 * 不能使用任何内置的库函数，如  sqrt 。
 * 输入：num = 16
 * 输出：true
 * 解释：返回 true ，因为 4 * 4 = 16 且 4 是一个整数。
 * @author ygt
 * @since 2024/8/12
 */
public class IsPerfectSquare {
    public static void main(String[] args) {
        int num = 13;
        System.out.println("有效的完全平方数：" + new IsPerfectSquare().isPerfectSquare(num));
    }

    /*方式：二分查找的模板*/
    public boolean isPerfectSquare(int num) {
        int left = 0, right = num;
        // 思路与上一道题（x 的平方根）类似，判断中间值的平方与x的大小，然后不断缩小上下界的范围。
        // 区别在于 平方后要精准相等，才是有效的完全平方数。
        while(left <= right) {
            int mid = (right - left) / 2 + left;
            long value = (long)mid * mid;
            if(value < num) {
                left = mid+1;
            }else if(value > num){
                right = mid - 1;
            }else {
                return true;
            }
        }
        return false;
    }
}

小结算法

今天的算法还是相对比较简单，很好刷，认真思考下，就可以完成的。

补充一下自己的面试题

• jvm的内存区域 📍

• 对象的创建过程📍

• 对象的内存布局📍

• 对象的访问方式 📍

• 晋升老年代的条件📍

• 空间分配担保机制📍

jvm的内存区域

VM的内存区域可以划分为以下两个部分，一块是线程私有的，其中包括着程序计数器、虚拟机栈和本地方法栈；还有一块是线程共享的，其中包含着堆和方法区。

• 程序计数器：

  是一块较小的内存空间，主要作用是记录当前线程所执行字节码指令的行号指示器，因为线程是会不断切换的，程序计数器就是来保证切换到当前线程后可以执行到正确的字节码指令。

• 虚拟机栈：

  主要作用是管理Java方法的调用，每个方法被执行的时候，虚拟机都会同步创建一个栈帧，每一个方法被调用直至执行完毕的过程，就对应着一个栈帧在虚拟机栈中入栈和出栈的操作；

  一个栈帧中主要有几个部分，分别是局部变量表、操作数栈、动态链接、方法返回地址和一些附加信息：

  • 局部变量表：主要用于存储方法参数和定义在方法体内的局部变量，主要包括基本数据类型、引用类型和返回类型，这些数据类型在局部变量表中以slot变量槽表示，其中long、double类型会占用两个slot，其余数据类型占用一个slot。局部变量中的变量只在当前方法即当前栈帧中有效，在方法调用结束后，随着栈帧出栈，局部变量表也会随之销毁；
  • 操作数栈：主要用于在方法执行过程中，根据字节码指令，通过入栈和出栈的操作，在栈中写入数据或者读取数据，或者使用操作数栈来实现结果的运算如求和，复制等操作，其中long和double数据类型也是占用两个栈容量，而其他数据类型占用一个栈容量；
  • 动态链接的主要作用是将符号引用转换为内存的直接引用；
  • 方法返回地址：方法退出之后，会返回到最初方法被调用时的位置，在这过程中，有可能会有返回值传递给上层的方法调用者；
  • 附加信息：栈帧中还允许携带与Java虚拟机实现相关的一些附加信息。

• 本地方法栈：

  与虚拟机栈的作用类似，主要区别在于，虚拟机栈主要管理Java方法的调用，而本地方法栈主要管理本地Native方法的调用。

• 堆：

  • 是虚拟机中内存最大一块区域，是所有线程共享的区域，也是垃圾收集器管理的最重要的一块区域；

  • 堆的主要作用是存放管理对象实例，几乎所有对象实例都会在堆上分配；

  • 堆内存可以通过jvm参数-Xms或者-Xmx来设定堆的初始大小或者最大大小，来实现可扩展或者固定大小的状态；

  • 从回收内存角度来看，堆基于分代收集理论可以这样划分内存：

    新生代和老年代，二者默认比例大小为1:2，新生代主要存放是大多数情况下新创建对象，因为绝大多数对象都是朝生夕死的，而老年代主要存放年龄达到阈值的对象或者一些大对象。

    其中新生代中包含着eden区、survivor0区和survivor1区，三者默认比例大小为8:1:1

• 方法区：

  • 主要作用是用于存储被虚拟机加载的类型信息、域信息、方法信息、常量、静态变量等数据；
  • 在1.8之前，方法区叫做永久代，而在1.8之后，永久代被使用本地内存的元空间所取代，主要原因在于永久代存在虚拟机自身的内存管理的限制，而元空间是使用本地内存进行管理，可以根据应用程序需求更好的动态分配内存，元空间相对于永久代来说具有更好的内存管理、更高的性能和更灵活的特性，能够更好地满足现代应用程序的需求。因此，虚拟机选择使用元空间替代永久代。

对象的创建过程了解吗

当虚拟机接收到new指令后，会做以下几个步骤：

1. 类加载检查：

   首先会先检查这个类是否已经被加载了，如果这个类没有被类加载器加载的话，就必须先执行对应的类加载过程，对象的内存大小也在类加载完成后就确定；

2. 分配内存：

   在对象内存大小确定后，就可以在堆中划分对应大小的内存给新生对象，通常堆内存的存储情况会分为以下两种：

   • 堆内存是规整的，所有被使用过的内存存放一边，未使用的内存存放另一边，中间使用一个指针作为内存分界点的指示器，分配内存时，指针朝着未使用内存方向移动一段与新生对象内存大小相等的距离即可，这种方式叫做指针碰撞方式；
   • 堆内存是不规整的，已使用内存和未使用内存相互交错在一起，此时没办法使用上面的指针碰撞方式来分配内存，这时jvm会创建一个空闲列表来维护未使用内存空间，在分配内存时，从空闲列表中寻找一块合适的内存空间划分给新生对象即可，并更新空闲列表，这种方式叫做空闲列表；
   • 具体选择哪种分配方式取决于堆内存是否规整，而堆内存是否规整取决于jvm所使用的垃圾回收器。

3. 处理并发问题：

   因为堆是线程共享的，堆中对象的创建也是非常频繁的，在并发情况下，会有可能产生并发问题，为了解决并发问题，jvm通常有两个方式：

   • 采用CAS加失败重试的操作，来保证操作的原子性；
   • 将内存分配方式按照线程划分在不同的内存空间中进行，也就是为每一个线程在堆中创建一小块内存，每个线程创建对象都在自己的内存空间上进行，这块内存空间叫做TLAB，本地线程分配缓冲区，虚拟机是否使用TLAB，取决于jvm参数UseTLAB是否启用；

4. 初始化零值：

   在内存分配完成后，虚拟机就会将对象的属性进行默认初始化零值操作，保证了对象的实例字段可以在Java代码中不赋初始值就可以直接使用。

5. 设置对象头：

   虚拟机还会对对象进行必要的设置，如设置对象的哈希码，gc年龄分代信息以及一些锁信息，还有关于对于对象本身的类元数据的指针，这些都会存储在对象头中。

6. 执行init方法：

   最后会执行构造器方法，对对象的属性进行赋值操作。

对象的内存布局知道吗

对象在堆内存的存储布局可以分为三部分：对象头、实例数据、对齐填充。

对象头中包括以下几部分：

• markword：用于存储对象本身的运行时数据，主要包括哈希码、GC分代年龄、锁状态标志、线程持有的锁、偏向线程ID和偏向时间戳；
• KlassWord：用于存储对象本身的类元数据的指针，通过这个指针可以确定这个对象是哪个类的实例；
• array length：如果对象是数组，才会包含这一部分，用于记录数组的长度。

实例数据：存储对象的属性字段，包含了父类的属性字段。

对齐填充：起着占位符的作用，因为虚拟机要求对象地址必须是8字节的整数倍，所以如果不够8字节的整数倍，就会产生padding，来补全8字节的整数倍。

对象的访问方式

对象的访问方式有两种，句柄访问和直接指针访问。

句柄访问：

会从堆中开辟一个句柄池，来存储对象的对象实例数据与类型数据的地址信息，其中对象本身只存储实例数据，同时栈上引用指向句柄池。

直接指针访问：

对象本身会存储实例数据以及类型数据，栈上引用直接指向对象本身，不需要多一次间接访问的开销。

优缺点的话：

使用句柄来访问的最大好处就是引用中存储的是稳定的句柄地址，当对象应该垃圾收集而被移动时只会改变句柄中的实例数据指针，而reference本身不需要被修改；

而使用直接指针访问对象最大的好处就是速度快，它节省了一次指针定位的时间开销。

虚拟机本身是用直接指针访问方式。

晋升老年代的条件

1. 大对象直接晋升老年代：

   在Serial 和 ParNew 两款新生代收集器中提供了一个jvm-XX:PretenureSizeThreshold 的参数，默认是0，如果设置了值，只要大于等于该值的对象直接在老年代分配，而在其他收集器中，默认的话，大约差不多在eden区大小80%左右就会直接在老年代分配。

2. 长期存活的对象进入老年代：

   如果一个对象在eden区创建并在一次young gc后还存活，并且能被Survivor区容纳的话，这个对象就会复制到Survivor区，对象本身的年龄计数就会加一，随着多次垃圾收集，年龄增加到一定阈值，默认是15，就会晋升到老年代中。

3. 动态对象年龄判定：

   如果在survivor空间中相同年龄的所有对象总和大小大于survivor空间大小的一半，年龄只要大于等于该年龄的对象就会晋升到老年代。

空间分配担保机制

在jdk1.6及之前是这样的：

在给对象分配内存时，eden区空间不够了，要触发young gc前，就会尝试让老年代进行担保：

1. 虚拟机首先会检查老年代最大可用连续空间大小是否大于新生代所有对象大小，如果条件成立，直接young gc；
2. 如果不成立，虚拟机就会先查看是否启用了允许担保失败机制的参数，如果没启用，就直接full gc；
3. 启用了的话，就会判断老年代最大可用连续空间大小是否大于历次晋升到老年代对象的平均大小，如果小于，就直接full gc；
4. 如果大于，就会尝试young gc；
5. 在以上young gc过程，会有以下三种情况：
   • YoungGC后，存活对象小于survivor大小，此时存活对象进入survivor区中；
   • YoungGC后，存活对象大于survivor大小，但是小于老年代可用空间大小，此时直接进入老年代；
   • YoungGC后，存活对象大于survivor大小，也大于老年代可用空间大小，就会触发full gc。
6. 最后，如果full gc后，还不能存放对象，就会报oom。

在jdk1.7及之后的话，取消了允许担保失败机制的参数，直接就判断老年代最大可用连续空间大小是否大于新生代所有对象大小或者是否大于历次晋升到老年代对象的平均大小，满足一项，就直接young gc，否则触发full gc。

明日内容

基础面试题

下面的题目的答案是基于自己的理解和思考去编写出来的，也希望大家如果看到了，可以根据自己的理解去转换为自己的答案。

当然很多思考也有参考别人的成分，但是自己能讲述出来就是最棒的。

这里有一篇阿里的jvm面试题

明天给自己的目标是，二倍速过一下jvm的视频，能过多少算多少。

判断对象仍然存活

判断对象是否存活有两种方法：

1. 引用计数法：

   为每个对象维护一个引用计数器，每当该对象被引用时，计数器加一，引用失效，计数器减一。所以一个对象的引用计数器不为0，代表存活，为0代表为垃圾对象。

   引用计数法存在一个循环引用的问题，当两个或者多个对象互相引用的时候，他们计数器不会为0，就算是真的成为了垃圾对象，也不会被回收。

2. 可达性分析算法：

   相对于引用计数法，可达性分析算法可以有效解决引用计数法中的循环引用问题，它的主要判断步骤有：

   以GCRoots的根对象作为起始结点集，从这些结点开始，根据引用关系向下搜索，搜索被根对象集合所连接的目标对象是否可达，

   只有能够被根对象集合直接或间接连接的对象才是存活对象，而没有任何引用链相连的对象，则是不可达的，代表为垃圾对象。

   常见的GCRoots类型有：虚拟机栈中本地变量表对象、静态变量、常量、类加载器。

引用类型有哪些

引用类型分为四种，强引用、软引用、弱引用、虚引用。

• 强引用：

  在Java中默认声明的创建对象就是强引用，只要被强引用关联的对象，就不会被回收；

• 软引用：

  如果内存足够，不会回收软引用对象，如果内存不够了，就会回收软引用对象；

• 弱引用：

  只能够存活于下个gc前，也就是弱引用有没有被引用，都会被回收；

• 虚引用：

  随时都会被回收，唯一目的就是了能在这个对象被收集器回收时收到一个系统通知。

垃圾收集算法

在通过可达性分析算法，区分了存活对象和垃圾对象，就会执行垃圾回收，释放垃圾对象占用的空间。

• 标记清除算法：

  它包括两个阶段，标记和清除阶段，分别为：

  标记：通过根对象开始遍历整个对象图，并标记与根对象直接或间接相关联的对象为存活对象；

  清除：通过对堆内存遍历扫描，清除回收未被标记为存活对象的垃圾对象。

  标记清除算法会产生内存碎片问题，需要额外维护一个空闲列表，而且可能当大对象存储时，可能无法得到足够的连续空闲空间，从而触发另一个垃圾收集动作。适用于老年代。

• 复制算法：

  将可用的内存空间分为两个相等大小的空间，每次只使用其中一块称作活动区域，另一块被闲置的称作闲置区域，每次活动区域内存不够了，就会将存活的对象一次性复制到闲置区域中，清除掉活动区域的垃圾对象，随后两个区域互换角色。

  比较明显的缺点就是会造成空间浪费，适用于新生代。

• 标记整理算法：

  它分为两个阶段，标记和整理阶段，分别为：、

  标记：通过根对象开始遍历整个对象图，并标记与根对象直接或间接相关联的对象为存活对象；

  整理：将存活对象移动到堆内存的一端，按照顺序依次排列，移动过程中，更新对象的引用关系，最后清理边界外的内存。

三色标记法

三色标记法是指在并发情况下，进行可达性分析时，不需要停顿用户线程，可以让用户线程和垃圾收集线程并发执行，引出的一个并发标记算法。

三色标记法是通过将对象是否被访问过，来分为三个不同的颜色来跟踪它们的状态，从而确定哪些对象是垃圾对象，可以被回收的

• 白色：表示该对象没有被标记过，如果整个可达性分析结束后，对象仍然是白色的，就代表不可达，是垃圾对象；
• 灰色：表示该对象已经被标记过，但是该对象还有引用没有被标记过，中间过渡的状态；
• 黑色：表示该对象已经被标记过并且该对象的引用也标记过了，黑色对象代表可达，存活对象。

标记过程：

1. 初始时，所有对象都是白色的，都在白色集合中；
2. 将GC Rooots根对象直接引用的对象，标记为灰色，移动到灰色集合中；
3. 不断从灰色集合中取出灰色对象，向下查找引用对象，找到引用对象就标记灰色，移动到灰色集合中，不管有没有找到引用对象，灰色对象都将标记为黑色；
4. 直至灰色集合中为空为止，最后仍为白色对象的，就是不可达的，是垃圾对象，可以回收。

并发问题：

因为在并发标记过程中，用户线程也是在运行的，此时对象的引用关系可能就会发生改变，导致出现多标或者漏标的问题。

多标：是指在并发标记过程，一个已经被标记为黑色或者灰色对象，此时变成了垃圾了，由于不会再对该对象重新扫描，就会产生本应该回收的对象没有回收，这个对象也就是浮动垃圾，浮动垃圾对系统影响不大，待下次gc回收即可。

漏标：是指在并发标记过程，一个白色对象原本被灰色对象所引用，但是用户线程删掉了灰色对象的引用白色对象，重新让一个黑色对象引用了这个白色对象，由于黑色对象不会重新扫描，就会这个对象原本应该存活，导致被当做垃圾对象而清除了，这就会使系统出现问题。

为此这个并发问题是需要解决的，为此垃圾收集器提供了两种解决方案：增量更新和原始快照。

增量更新破坏的是增加引用的条件，当黑色对象插入新的指向白色对象的引用关系时，就将这个新插入的引用记录下来，等并发扫描结束之后，再将这些记录过的引用关系中的黑色对象为根，重新扫描一次。

原始快照破坏的是删除引用的条件，当灰色的对象要删除指向白色对象的引用时，就将这个要删除掉的引用记录下来（即拍下快照），在并发扫描就结束之后，再以这些记录过引用关系的灰色对象为根，重新扫描一次。

原始快照相对增量更新来说效率更高，因为不需要在重新标记阶段再次深度扫描被删除引用对象，但是可能造成浮动垃圾。

详细说下CMS收集器吗

CMS是以获取最短回收停顿时间为目标的垃圾收集器，采用了标记-清除算法，实现让垃圾收集线程和用户线程同时工作的并发收集器。

CMS的执行过程中，还有一些可选的阶段，详细的工作流程可以分为七个步骤：初始标记、并发标记、并发预清理、可中断的并发预清理、重新标记、并发清除和并发重置，其中只有初始标记和重新标记需要STW。

• 初始标记：

  单线程运行，以GC Roots为起点进行可达性分析，标记仅能被GC Roots能直接关联的对象和遍历新生代对象能关联的老年代对象，需要STW；

• 并发标记：

  从GC Roots根对象直接关联对象开始遍历整个对象图，标记可达对象，这个过程无需STW，可以与用户线程一起并发执行；

• 并发预清理：

  在并发标记过程中，因为用户线程和垃圾线程是同时运行的，此时就很有可能发生引用关系的变更，随时都有可能新生代对象晋升到老年代，老年代的对象的引用关系发生改变等等，因为虚拟机采用了卡表的记忆集来管理老年代的内存，当对象引用发生变化事，将对象所在的卡页进行标记为脏页，这一阶段主要就是处理这些脏页的产生，这一阶段也是可选的，主要通过CMSPrecleanEnabled参数控制启用或者关闭，默认是启用的；

• 可中断的并发预清理：

  这一阶段主要处理新生代指向老年代的信用，从而让老年代中一些未被标记的对象称为活跃对象，这一阶段在eden区空间使用率超过2M时就会执行该阶段，而在eden区空间使用率大于50%就会中断该阶段或者在执行时间超过了5s也会中断该阶段，直接执行重新标记，这一阶段中也会触发一次Young gc，来降低扫描新生代对象的存活对象。

• 重新标记：

  在并发过程中，用户线程始终在运行，因此对象引用关系随时发生变更：

  1. 新生代对象晋升到老年代；
  2. 老年代未标记对象被新生代对象引用；
  3. 已标记对象增加了对未标记对象的引用；
  4. 已标记对象的引用被删除。

  这些情况中，产生漏标会导致存活对象当做垃圾被清理掉，最主要就是通过增量更新来保证漏标问题，以及处理脏页来确保跨代引用，主要有以下工作：

  在上面也讲解在CMS中，通过增量更新来确保漏标的问题，还有使用卡表来确保跨代引用的问题。所以重新标记阶段，jvm 主要进行以下三个工作：

  1. 遍历新生代对象，重新标记被引用的老年代对象；
  2. 从 GC Roots 出发，重新标记被引用修改过的老年代对象；
  3. 遍历卡表，对脏页内的老年代对象进行重新标记。

• 并发清理：

  清理删除掉标记阶段判断的已经死亡的对象，由于不需要移动存活对象，所以这个阶段也是可以与用户线程同时并发的，可能会产生浮动垃圾，最后需要使用空闲列表来维护可用空间。

• 并发重置：

  完成了整个 CMS 的标记-清除工作后，需要将 CMS 算法的内部数据进行重置，从而让下一次 GC 顺利开始。

CMS可能有以下弊端：

• 处理器资源敏感：

  CMS收集器是比较消耗CPU资源的，对处理器资源是比较敏感的，因为在垃圾收集阶段，它虽然不会导致用户线程停顿，但却会因为占用了一部分线程（垃圾线程）而导致应用程序变慢，降低总吞吐量。

• 无法处理“浮动垃圾”：

  因为在垃圾收集阶段，用户线程是还在继续运行的，程序在运行自然就还会伴随有新的垃圾对象不断产生，CMS无法在当次收集中处理掉它们，只好留待下一次垃圾收集时再清理掉。为此，有可能出现 Con-current Mode Failure 失败进而导致另一次完全STW的Full GC的产生，冻结用户线程的执行，临时启用Serial Old收集器来重新进行老年代的垃圾收集， 但这样停顿时间就很长了。

• 内存碎片：

  因为CMS是一款基于标记-清除算法实现的收集器，标记-清除会产生内存碎片。

详细说下G1垃圾收集器

G1开创了面向局部收集的设计思路以及基于Region的内存布局形式，并且拥有可预测的停顿时间模型，确保在指定最大停顿时间上完成垃圾回收。

内存布局：

G1将堆内存划分为多个大小相等的独立区域Region，每一个Region都可以根据需要扮演不同类型：

1. Eden – 新生代
2. Survive – 幸存区
3. Old – 老年代
4. Humongous – 巨大对象存储区

每个Region的大小可以通过参数-XX：G1HeapRegionSize设定，取值范围为1MB～32MB，且应为2的N次幂。其中只要大小超过了一个Region容量一半的对象即可判定为大对象。而对于那些超过了整个Region容量的超级大对象， 将会被存放在N个连续的Humongous Region之中，G1的大多数行为都把Humongous Region作为老年代的一部分来进行看待。

停顿模型：

基于Region的停顿时间模型是G1能够建立可预测的停顿时间模型的前提。G1将Region作为单次回收的最小单元，即每次收集到的内存空间都是Region大小的整数倍，这样可以有计划地避免在整个Java堆中进行全区域的垃圾收集。具体思路是：

G1收集器会去跟踪各个Region里面的垃圾堆积的价值大小，价值即回收所获得的空间大小以及回收所需时间的经验值，然后在后台维护一个优先级列表，每次根据用户设定允许的收集停顿时间（使用参数-XX：MaxGCPauseMillis指定，默认值是200毫秒），优先处理回收价值收益最大的那些Region。

跨Region引用对象

在之前的垃圾收集器中，我们也讲过跨代引用的问题，主要就是新生代中存在对老年代对象的引用，或者老年代中存在对新生代的引用。而现在G1将Java堆分成多个独立Region后，多个Region肯定也会存在互相引用的现象，那现在要怎么解决呢？

实际上还是需要通过使用记忆集避免全堆作为GC Roots扫描，但在G1收集器上记忆集的应用其实要复杂很多，它的每个Region都维护有自己的记忆集，这些记忆集会记录下别的Region指向自己的指针，并标记这些指针分别在哪些卡页的范围之内。

G1的记忆集在存储结构的本质上是一种哈希表，Key是别的Region的起始地址，Value是一个集合，里面存储的元素是卡表的索引号。这里不仅需要记录谁引用了我，还需要记录我引用了谁，所以会比原来的卡表实现起来更复杂，同时由于Region数量比传统收集器的分代数量明显要多得多，因此G1收集器要比其他的传统垃圾收集器有着更高的内存占用负担。G1至少要耗费大约相当于Java堆容量10%至20%的额 外内存来维持收集器工作，这可以说是G1的缺陷之一。

对象引用关系改变

除了跨Region引用对象的问题，还有在并发标记阶段如何保证收集线程与用户线程互不干扰地运行呢？

1. 用户线程改变对象引用关系时，必须保证其不能打破原本的对象图结构，导致标记结果出现错误（漏标）：在CMS收集器中采用增量更新算法实现，而G1收集器则是通过原始快照（SATB）算法来实现的；
2. 垃圾收集对用户线程的影响还体现在回收过程中新创建对象的内存分配上，程序要继续运行就肯定会持续有新对象被创建：G1为每一个Region设计了两个名为TAMS（Top at Mark Start）的指针，把Region中的一部分空间划分出来用于并发回收过程中的新对象分配，并发回收时新分配的对象地址都必须要在这两个指针位置以上。G1收集器默认在这个地址以上的对象是被隐式标记过的，即默认它们是存活的，不纳入回收范围。与CMS中的Concurrent Mode Failure失败会导致Full GC类似，如果内存回收的速度赶不上内存分配的速度，G1收集器也要被迫冻结用户线程执行，导致Full GC而产生长时间STW 。

工作流程

如果我们不去计算用户线程运行过程中的动作（如使用写屏障维护记忆集的操作），G1收集器的运作过程大致可划分为以下四个步骤：

• 初始标记（Initial Marking）：仅仅只是标记一下GC Roots能直接关联到的对象，并且修改TAMS指针的值，让下一阶段用户线程并发运行时，能正确地在可用的Region中分配新对象。这个阶段需要停顿线程，但耗时很短，而且是借用进行Minor GC的时候同步完成的，所以G1收集器在这个阶段实际并没有额外的停顿。
• 并发标记（Concurrent Marking）：从GC Root开始对堆中对象进行可达性分析，递归扫描整个堆里的对象图，找出要回收的对象，这阶段耗时较长，但可与用户程序并发执行。当对象图扫描完成以后，还要重新处理SATB记录下的在并发时有引用变动的对象。
• 最终标记（Final Marking）：对用户线程做另一个短暂的暂停，用于处理并发阶段结束后仍遗留下来的最后那少量的SATB记录。
• 筛选回收（Live Data Counting and Evacuation）：负责更新Region的统计数据，对各个Region的回收价值和成本进行排序，根据用户所期望的停顿时间来制定回收计划，可以自由选择任意多个Region构成回收集，然后把决定回收的那一部分Region的存活对象复制到空的Region中，再清理掉整个旧Region的全部空间。这里的操作涉及存活对象的移动，是必须暂停用户线程，由多条收集器线程并行完成的。

从上述阶段的描述可以看出，G1收集器除了并发标记外，其余阶段也是要完全暂停用户线程的。

G1在逻辑上仍然采用了分代的思想，从整体来看是基于「标记-整理」算法实现的收集器，但从局部（两个Region之间）上看又是基于「标记-复制」算法实现。

算法

明天继续，把数组的刷完，接着后天就进入链表的环节，链表个人是有基础的，完全可以不用看视频去额外增加学习的成本。

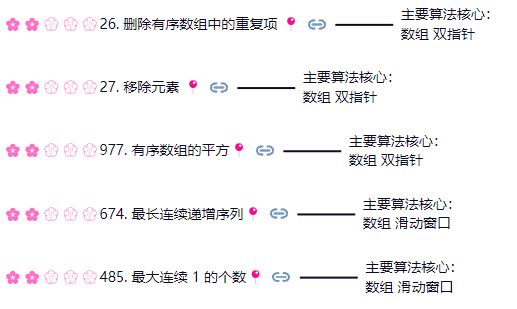
需要有滑动窗口的思想基础，最后还是决定从我看的算法基础教程里，刷到链表的视频，以便快速进入链表刷题的节奏。

• 删除有序数组中的重复项 📍
• 移除元素📍
• 有序数组的平方📍
• 最长连续递增序列📍
• 最大连续 1 的个数📍

加强面试题

暂时应该没时间额外思考下加强面试题，明天就先没有，得先把基础打牢了，夯实基础，稳步前行。无论是学习还是工作，扎实的基础是成功的关键。

🌸 完结

最后，相关算法的代码也上传到gitee或者github上了。

乘风破浪会有时 直挂云帆济沧海

希望从明天开始，一起加油努力吧，成就更好的自己。

🥂 虽然这篇文章完结了，但是我还在，永不完结。我会努力保持写文章。来日方长，何惧车遥马慢！✨✨✨

💟 感谢各位看到这里！愿你韶华不负，青春无悔！让我们一起加油吧！ 🌼🌼🌼

💖 学到这里，今天的世界打烊了，晚安！🌙🌙🌙