给你一个长度为 n 的数组 nums 和一个 正 整数 k 。

如果 nums 的一个
子数组
中，第一个元素和最后一个元素 差的绝对值恰好 为 k ，我们称这个子数组为 好 的。换句话说，如果子数组 nums[i…j] 满足 |nums[i] - nums[j]| == k ，那么它是一个好子数组。

请你返回 nums 中 好 子数组的 最大 和，如果没有好子数组，返回 0 。

示例 1：
输入：nums = [1,2,3,4,5,6], k = 1
输出：11
解释：好子数组中第一个元素和最后一个元素的差的绝对值必须为 1 。好子数组有 [1,2] ，[2,3] ，[3,4] ，[4,5] 和 [5,6] 。最大子数组和为 11 ，对应的子数组为 [5,6] 。

示例 2：
输入：nums = [-1,3,2,4,5], k = 3
输出：11
解释：好子数组中第一个元素和最后一个元素的差的绝对值必须为 3 。好子数组有 [-1,3,2] 和 [2,4,5] 。最大子数组和为 11 ，对应的子数组为 [2,4,5] 。

示例 3：
输入：nums = [-1,-2,-3,-4], k = 2
输出：-6
解释：好子数组中第一个元素和最后一个元素的差的绝对值必须为 2 。好子数组有 [-1,-2,-3] 和 [-2,-3,-4] 。最大子数组和为 -6 ，对应的子数组为 [-1,-2,-3] 。

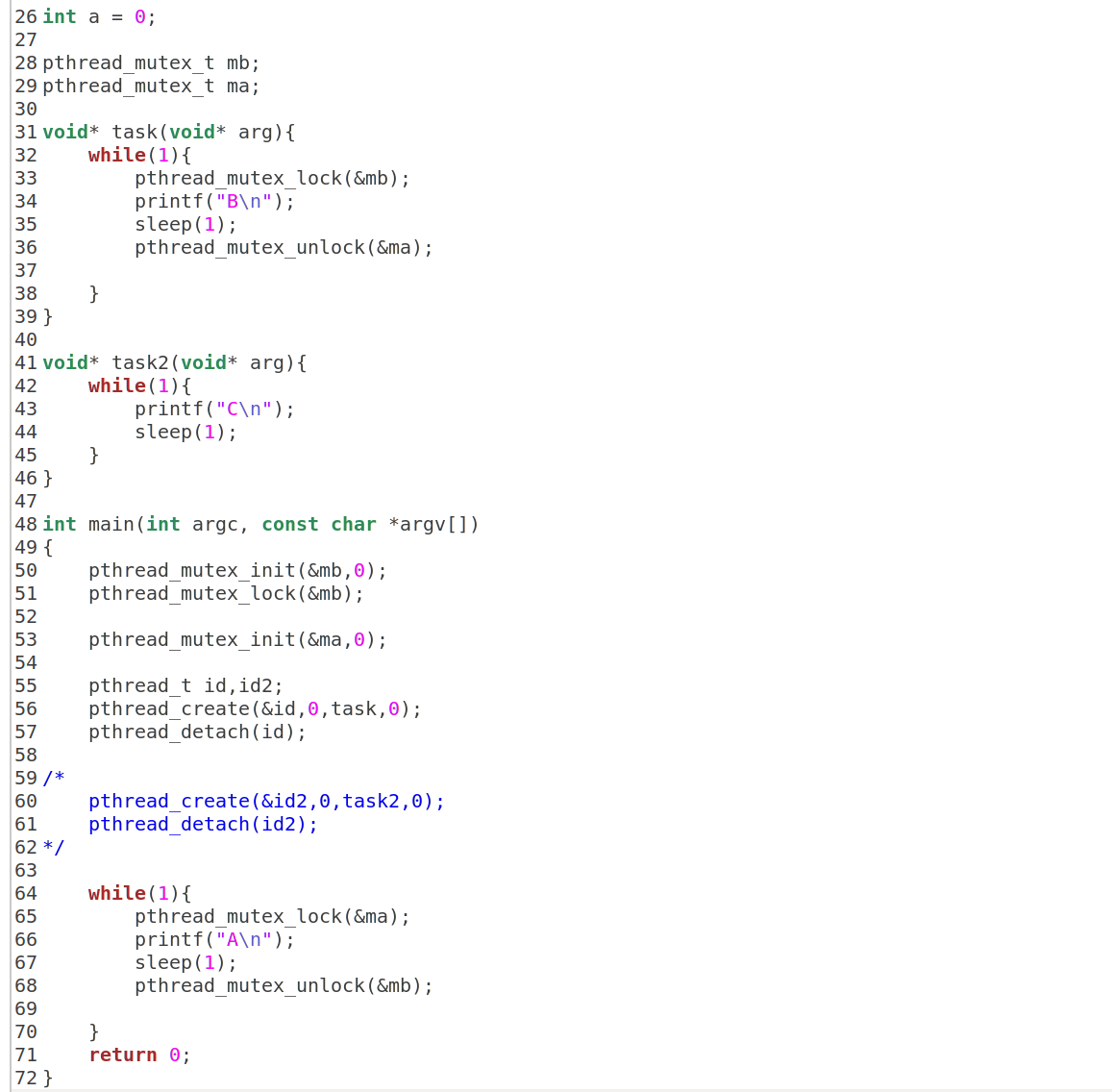
暴力求解（超时）

class Solution {
public:
    long long maximumSubarraySum(vector<int>& nums, int k) {
        vector<long long> group(nums.size());
        
        long long sum = 0;
        for(int i = 0;i < nums.size(); i++){
            sum += nums[i];
            group[i] = sum;
        }

        long long ans = INT_MIN;
        bool flag = false;
        for(int i = 0;i < nums.size()-1;i++){
            for(int j = i+1;j < nums.size();j++){
                if(abs(nums[j] - nums[i]) == k){
                    flag = true;
                    ans = max(ans, group[j] - (i > 0 ? group[i-1] : 0));
                }
            }
        }
        if(!flag){
            ans = 0;
        }
        return ans;
    }
};

暴力方法超时。

前缀和 + 哈希

class Solution {
public:
    long long maximumSubarraySum(vector<int>& nums, int k) {
        long long ans = LLONG_MIN, sum = 0;
        unordered_map<int,long long> group;
        //枚举j
        for(int x : nums){
            auto it = group.find(x - k);
            if(it != group.end()){
                ans = max(ans, sum + x - it->second);
            }

            it = group.find(x + k);
            if(it != group.end()){
                ans = max(ans, sum + x - it->second);
            }

            it = group.find(x);
            if(it == group.end() || sum < it->second){
                group[x] = sum;
            }

            sum += x;
        }
        return ans == LLONG_MIN ? 0 : ans;
    }
};

时间复杂度：O(n)
空间复杂度：O(n)

首先是通过变形来转换问题，在上一个解法中，需要枚举i，在for中继续枚举j，来找出nums[j] - nums[i] = k的情况。这样使得时间复杂度很高，这时候可以想到，由于哈希表有非常强的查找性能，时间复杂度为O(1)，所以可以将问题转换成枚举 j，然后通过 nums[j] - k来找到nums[i]。

我们将nums[i]储存在哈希表的键， 这时候我们就可以快速来找到对应的nums[i]，然后那么哈希表的值就可以用来储存nums[i]的前缀和。并且我们要让符合条件的子段和尽可能大，所以nums[i]的前缀和要尽可能小，所以在储存nums[i]的前缀和的时候，如果有比他小的前缀和，就将哈希表中对应的值替换成最小的前缀和。

需要注意的是，在解法2中，另前缀和s[0] = 0，这也意味着这次子段和的计算方式不是s[j] - s[i-1]，而是s[j+1] - s[i]，也就是前缀和的索引方式整体往右挪了一位。