基于sklearn的机器学习 — 支持向量机（SVM）

支持向量机（SVM：support vector machine）另一种功能强大、应用广泛的学习算法，可应用于分类、回归、密度估计、聚类等问题。SVM可以看作是感知器（可被视为一种最简单形式的前馈神经网络，是一种二元线性分类器）的扩展，与逻辑回归相比，支持向量机在学习复杂的非线性方程时提供了一种更为清晰，更加强大的方式。

SVM是一种监督式的学习方法，用统计风险最小化的原则来估计一个分类的超平面(hyperplane) ，其基础的概念非常简单，就是找到一个决策边界(decision boundary) ，让两类之间的边界(margins) 最大化，使其可以完美地分隔开来。

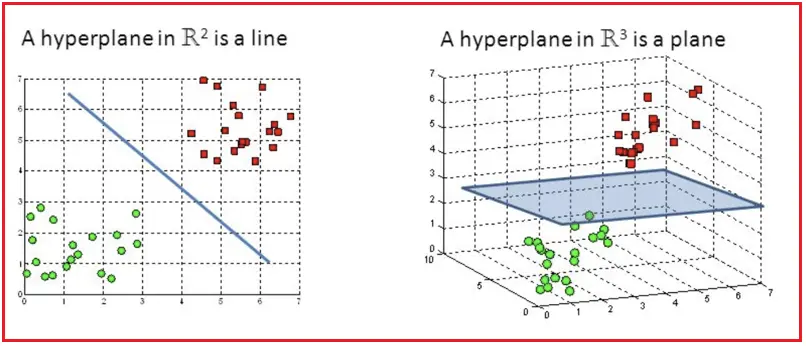
超平面(hyperplane) 是n维空间中的n - 1个子空间。例如，想要划分一个二维空间，需要使用一维超平面（即一条线），划分三维空间，需要使用二维超平面（即一张面），超平面只是将这一概念推广到 n 维空间。

不同维度下的超平面

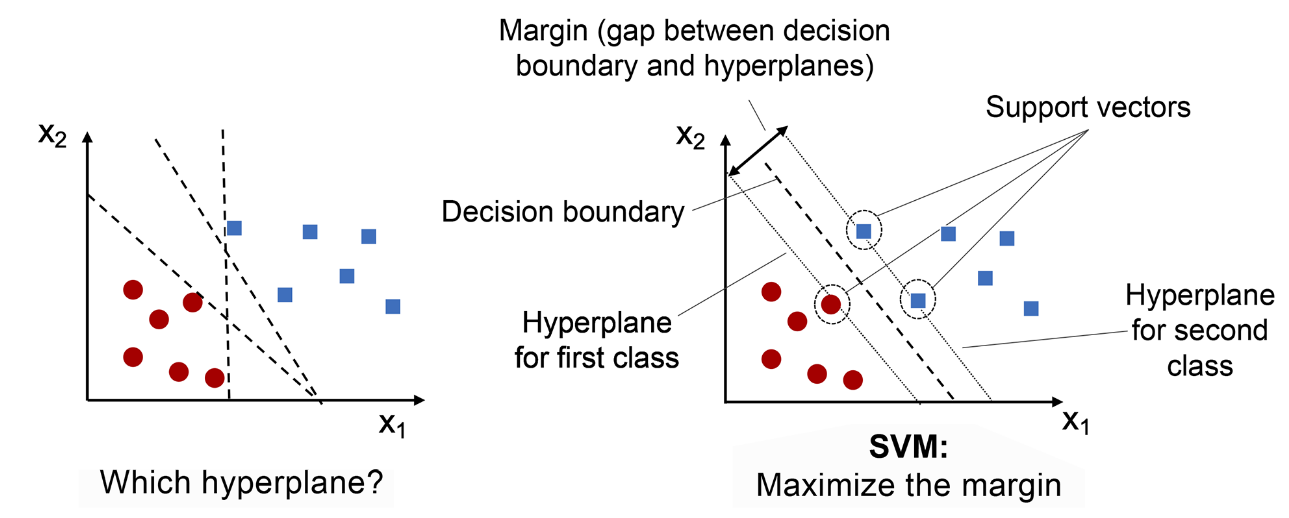
支持向量(support vectors) 指的是最接近超平面或超平面上的数据点，它们影响超平面的位置和方向。

边界(margin) 的定义是：分离超平面（决策边界）与最接近该超平面的训练实例（即支持向量）之间的距离。

支持向量与边界

1. 支持向量机的类型

支持向量机有两种类型：

线性支持向量机
非线性支持向量机

线性与非线性可分问题

1.1 线性支持向量机

线性SVM适用于训练数据近似线性可分的情况，在这种情况下，存在一个超平面可以将不同类的样本完全划分开。

使用支持向量分类器 (SVC：support vector classifier) 查找使类之间的边距最大化的超平面，scikit-learn 的 LinearSVC实现了一个简单的 SVC。

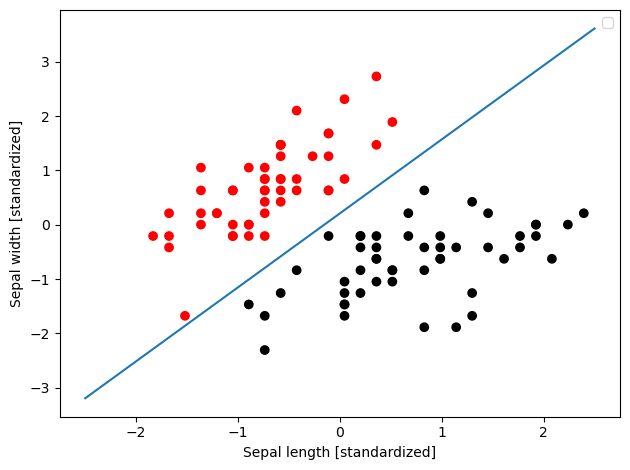
下面基于鸢尾花数据集，在二维空间上对两组数据进行分类，然后绘制超平面：

# Load libraries  
from sklearn.svm import LinearSVC 
from sklearn import datasets 
from sklearn.preprocessing import StandardScaler 
import numpy as np  

# Load data with only two classes and two features 
iris = datasets.load_iris() 
features = iris.data[:100,:2] 
target = iris.target[:100]  

# Standardize features  
scaler = StandardScaler() 
features_standardized = scaler.fit_transform(features)  

# Create support vector classifier 
svc = LinearSVC(C=1.0)  

# Train model  
model = svc.fit(features_standardized, target)

# Plot data points and color using their class  
color = ["red" if c == 0 else "black" for c in target] 
plt.scatter(features_standardized[:,0], features_standardized[:,1], c=color)

# Create the hyperplane 
w = svc.coef_[0] 
a = -w[0] / w[1] 
xx = np.linspace(-2.5, 2.5) 
yy = a * xx - (svc.intercept_[0]) / w[1]

# Plot the hyperplane 
plt.plot(xx, yy) 
plt.xlabel('Sepal length [standardized]')
plt.ylabel('Sepal width [standardized]')
plt.tight_layout()
plt.legend()
plt.show()

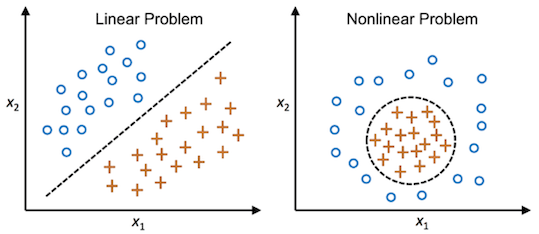
1.2 非线性支持向量机

对于线性不可分的问题，SVM可以借助核方法（Kernel methods）将样本从低维空间 (输入空间) 映射到高维空间 (特征空间) 来进行线性划分，从而解决非线性分类问题。

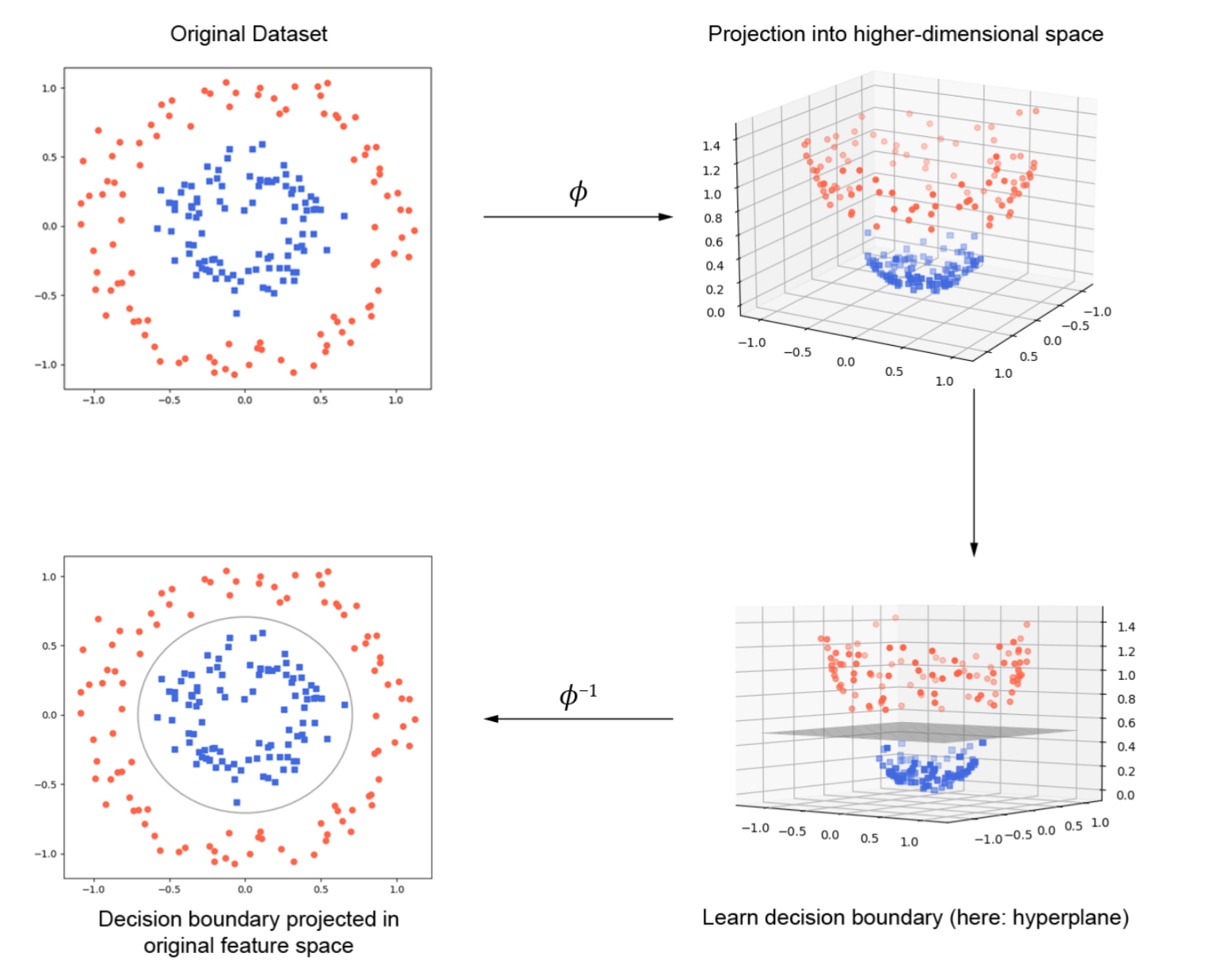
使用核方法对非线性数据进行分类的过程

上图展示了如何通过将数据投影到更高维度的空间来实现非线性可分数据的分类。

图中显示了一个二维平面上的数据集。红色圆点和蓝色方块代表两类数据，数据是非线性可分的，即没有一条直线可以将两类数据完美地分开。

通过使用映射函数（ $\phi$ ）将原始的二维数据投影到三维空间，在这个新的高维空间中，原本在二维空间中非线性可分的数据，现在在三维空间中变得线性可分。

在三维空间中，我们可以学习一个线性分类器（比如一个超平面）来将两类数据分开。

通过逆映射函数（ $\phi^{-1}$ ），将三维空间中的决策边界投影回原始的二维空间，投影回二维空间后的决策边界不再是直线，而是曲线，这条曲线能很好地将两类数据分开。

通过核方法可以将非线性可分的数据映射到高维空间，在高维空间中应用线性分类器，然后将高维空间中的分类结果逆映射回原始空间，从而实现非线性分类。

下面通过一个简单的例子来理解，首先创建一个非线性可分的数据集：

# Load libraries  
from sklearn.svm import SVC 
from sklearn import datasets 
from sklearn.preprocessing import StandardScaler 
import numpy as np  

# Set randomization seed 
np.random.seed(0)  

# Generate two features  
features = np.random.randn(200, 2)  

# Use an XOR gate to generate 
# linearly inseparable classes  
target_xor = np.logical_xor(features[:, 0] > 0, features[:, 1] > 0) 
target = np.where(target_xor, 0, 1)  

# Create a support vector machine with a radial basis function kernel 
svc = SVC(kernel="rbf", random_state=0, gamma=1, C=1)  

# Train the classifier  
model = svc.fit(features, target)

接着编写一个可以绘制二维空间的观测值和决策边界超平面的函数：

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
def plot_decision_regions(X, y, classifier, test_idx=None,  resolution=0.02):  
# setup marker generator and color map  
    markers = ('o', 's', '^', 'v', '<') 
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1  
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1  
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),  
                           np.arange(x2_min, x2_max, resolution))  
    lab = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)  
    lab = lab.reshape(xx1.shape)  
    plt.contourf(xx1, xx2, lab, alpha=0.3, cmap=cmap)  
    plt.xlim(xx1.min(), xx1.max())  
    plt.ylim(xx2.min(), xx2.max())
    for idx, cl in enumerate(np.unique(y)):  
        plt.scatter(x=X[y == cl, 0],  
                    y=X[y == cl, 1],  
                    alpha=0.8,  c=colors[idx],  
                    marker=markers[idx],  
                    label=f'Class {cl}',  
                    edgecolor='black')
        if test_idx:  
            # plot all examples  
            X_test, y_test = X[test_idx, :], y[test_idx]  
            plt.scatter(X_test[:, 0], X_test[:, 1], 
                        c='none', edgecolor='black', 
                        alpha=1.0,  linewidth=1, 
                        marker='o',  s=100, 
                        label='Test set')

上文创建的非线性数据集包含两个特征（即两个维度）和一个包含每个观测值类别的目标向量。

如果使用线性内核的支持向量机分类器进行分类：

# Create support vector classifier with a linear kernel 
svc_linear = SVC(kernel="linear", random_state=0, C=1)  

# Train model  
svc_linear.fit(features, target)  

# Plot observations and hyperplane  
plot_decision_regions(features, target, classifier=svc_linear) 
plt.legend()
plt.tight_layout()
plt.show()

可以看到，线性超平面的划分效果很差

现在将线性核函数换成径向基核函数，训练一个新模型：

# Create a support vector machine with a radial basis function kernel 
svc = SVC(kernel="rbf", random_state=0, gamma=1, C=1)

# Train the classifier  
model = svc.fit(features, target)

# Plot observations and hyperplane  
plot_decision_regions(features, target, classifier=svc) 
plt.legend()
plt.tight_layout()
plt.show()

划分结果为：

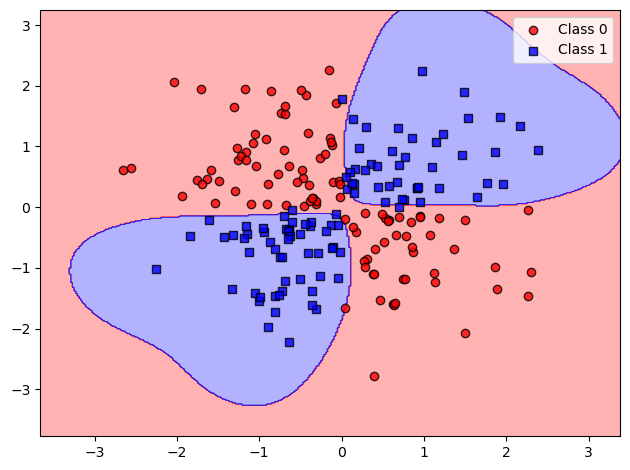
通过使用径向基核函数，可以创建一个更好的决策边界，这就是在支持向量机中使用核方法的目的。

在 scikit-learn中，我们可以通过kernel参数来选择要使用的核函数。

选择内核后，我们需要指定适当的内核选项，例如多项式内核（polynomial kernels）中的 d值，以及径向基函数内核中的γ值，还需要设置惩罚参数C。

在训练模型时，大多数情况下我们应该将所有这些参数都视为超参数，并使用模型选择技术来确定它们的组合值，以产生性能最佳的模型。

2. 计算预测概率

许多监督学习算法都使用概率估计来预测类别。SVC 使用超平面来创建决策区域，并不能自然地输出观测值属于某个类别的概率估计值。不过，我们可以输出经过校准的类别概率。

在具有两个类别的 SVC 中，可以使用普拉特缩放（Platt scaling）法，即首先训练 SVC，然后训练一个单独的交叉验证逻辑回归，将 SVC 输出映射为概率：

$P(y=1\mid x)=\frac{1}{1+e^{(A\times f(x)+B)}}$

式中：A 和 B 是参数向量， $f (x)$ 是第 i 个观测值距超平面的有符号距离。当我们有两个以上的类时，将使用普拉特缩放的扩展。

从更实际的角度来看，创建预测概率有两个主要问题：

由于我们要通过交叉验证来训练第二个模型，因此生成预测概率会大大增加训练模型所需的时间。
由于预测概率是通过交叉验证创建的，因此它们可能不总是与预测类别相匹配。也就是说，一个观测值可能被预测为类别 1，但预测为类别1的概率却小于 0.5。

在 scikit-learn 中，预测概率必须在训练模型时生成，我们可以将 SVC 的probability参数设置为 True，模型训练完成后，我们可以使用 predict_proba输出每个类别的估计概率。

# Load libraries  
from sklearn.svm import SVC 
from sklearn import datasets 
from sklearn.preprocessing import StandardScaler 
import numpy as np  

# Load data  
iris = datasets.load_iris() 
features = iris.data 
target = iris.target  

# Standardize features  
scaler = StandardScaler() 
features_standardized = scaler.fit_transform(features)  

# Create support vector classifier object  
svc = SVC(kernel="linear", probability=True, random_state=0)  

# Train classifier  
model = svc.fit(features_standardized, target)  

# Create new observation  
new_observation = [[.1, .2, .3, .4]]  

# View predicted probabilities  
model.predict_proba(new_observation)

3. 识别支持向量

支持向量机之所以得名，是因为超平面是由相对较少的观测数据决定的，这些观测数据被称为支持向量。

直观地说，超平面就是由这些支持向量所"承载 "，因此，这些支持向量对我们的模型非常重要。

如果我们从数据中移除一个不属于支持向量的观测值，模型不会发生变化；但如果我们移除一个支持向量，超平面就不会有最大边界。

因此有时需要确定哪些观测值是决策超平面的支持向量。

在我们基于鸢尾花数据集训练出SVC后，scikit-learn提供了许多用于识别支持向量的选项，可以使用support_vectors_来输出模型中的支持向量:

# Load libraries  
from sklearn.svm import SVC 
from sklearn import datasets 
from sklearn.preprocessing import StandardScaler 
import numpy as np  

# Load data with only two classes 
iris = datasets.load_iris() 
features = iris.data[:100,:] 
target = iris.target[:100]  

# Standardize features  
scaler = StandardScaler() 
features_standardized = scaler.fit_transform(features)  

# Create support vector classifier object 
svc = SVC(kernel="linear", random_state=0)  

# Train classifier  
model = svc.fit(features_standardized, target)

# View support vectors 
model.support_vectors_

结果有四个支持向量：

array([[-0.5810659 ,  0.42196824, -0.80497402, -0.50860702],
       [-1.52079513, -1.67737625, -1.08231219, -0.86427627],
       [-0.89430898, -1.4674418 ,  0.30437864,  0.38056609],
       [-0.5810659 , -1.25750735,  0.09637501,  0.55840072]])

另外，也可以使用support_查看支持向量的索引：

model.support_

运行后可得到上述四个支持向量的索引：

array([23, 41, 57, 98])

最后，可以使用n_support_来查找属于每个分类的支持向量的数量：

model.n_support_

结果为：

array([2, 2])

4. 不平衡问题

不平衡问题指的是在对样本进行分类过程中，需要更加重视某些类或某些单个样本的情况。

在支持向量机中，C是一个超参数，决定了对错误分类观测值的惩罚，处理不平衡类别的一种方法是按类别对C进行加权：

$C_{k}=C\times w_{j}$

其中，C是对错误分类的惩罚，w_j是与类别j的频率成反比的权重，C_k 是类别k的C值。

一般的想法是增加对错误分类少数类别的惩罚，以防止它们被多数类别 “淹没”。

在 scikit-learn 中，当使用 SVC 时，我们可以通过设置class_weight="balanced"自动设置C_k的值，平衡参数自动对类进行权重，使得：

$w_j=\frac{n}{kn_j}$

其中，w_j是j类的权重，n是观测值的数量，n_j是j类中观测值的数量，k是类的总数。

例如:

# Load libraries  
from sklearn.svm import SVC 
from sklearn import datasets 
from sklearn.preprocessing import StandardScaler 
import numpy as np

# Load data with only two classes 
iris = datasets.load_iris() 
features = iris.data[:100,:] 
target = iris.target[:100]  

# Make class highly imbalanced by removing first 40 observations 
features = features[40:,:] 
target = target[40:]  

# Create target vector indicating if class 0, otherwise 1 
target = np.where((target == 0), 0, 1)  

# Standardize features  
scaler = StandardScaler() 
features_standardized = scaler.fit_transform(features)  

# Create support vector classifier  
svc = SVC(kernel="linear", class_weight="balanced", C=1.0, random_state=0)  

# Train classifier  
model = svc.fit(features_standardized, target)