数组案例练习进阶版---对数组中的元素进行排序（冒泡法）

news2024/9/23 3:20:36

在上篇文章中，我们一起学习了常用排序法中的选择排序法，今天，我们将一起来学习新的排序方法——冒泡法排序

那么首先，什么是冒泡法呢？

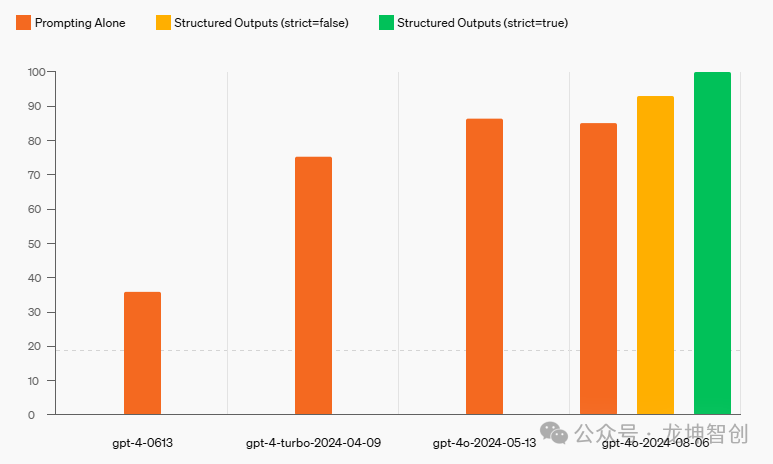
首先，第一列，我们有四个大小不一的球，我们称最下面的球为第一个球，最上面的为第四个球，首先我们从第一个球开始比较，也就是对黄色区域内的两个球进行大小比较，并把较大的那个球放到更上面的位置，这样一来，我们就得到了第二列小球

我们再从第二个小球开始比较，因此黄色区域也随之移动，现在第二个小球开始和第三个小球进行比较，同理，比较后，我们把更大的那个球与相对较小的球进行位置交换，使大球处于上方，然后我们就得到了第三列

第三列比较后，我们就得到了四个球中最大的那个球，我们把它置入红色区域，如第四列所示

现在我们忽略红色区域，利用剩下的小球继续进行第二轮比较，首先是还是一样，在第一列的黄色区域内我们把两个球进行比较，并把大球放在上面

现在来到第二列，可以看到，大球本身就在上面，因此我们不做任何操作

至此，这三个球中，最大的那个又出现了，我们把也把它和刚刚那个大球一起置入红色区域，即第三列

由于红色区域外还剩下两个球，因此我们进行第三轮比较，此时正好大球在上面，因此我们直接把它置入红色区域

此时，红色区域外已经只剩下一个球了，我们可以发现，球的顺序已经被排好了，因为排好的球特别像水里面冒的泡泡，因此，我们称这种排序方法为冒泡法排序

根据刚刚的分析，我们可以发现，4个球，只需要进行三轮比较，同理当数组长度为x时，我们只需对该数组中的数字进行x-1轮比较

不仅如此我们还可以得知，当进行第一轮比较时，红色区域还没有球，因此我们有四个球要比较，且只比较三次即可得到最大的球

第二轮比较时，红色区域有一个球了，因此我们只比较剩下的三个球即可，且只比较两次即可得到最大的球

我们的出结论，设需要比较的总球数为x，则比较的的次数始终为x-1，且每一轮比较，随着红色区域的扩大，x的值也随之减少

现在，我们设最外层循环为轮数,即：

for(int i=0;i<nums.length-1;i++){

如果有，5个数，数组长度就为5，我们就比较5-1=4轮，i的初值为0，每轮结束后，分别自增为1，2，3

为4时结束循环，而0，1，2，3正好四次

然后内层循环则为次数，即：

for(int i=0;i<nums.length-1;i++){
    for (int j=0;j< nums.length-1-i;j++){

j的初值为0，4个球只需比三次，同理如果有5个数，我们只需比四次，因此当j为0，1，2，3时正好四次，我们让j<5-1,即等于4时停止循环

为什么要减i呢？当第一轮时，红色区域为0，此时i也为0，第二轮时，i变为1，此时经过第一轮比较后，红色区域也正好为1，而我们每轮比较都要去掉红色区域的值，因此-i只是刚好凑巧能够满足需求。

好了，经过分析后，我们来看看代码：

public class Sort {
    public static void main(String[] args) {
        int[] nums = new int[]{28,43,16,35,27};//静态初始化数组
        int temp=0;//临时变量，用于交换值，否则会覆盖
        for(int i=0;i<nums.length-1;i++){//轮数
            for (int j=0;j< nums.length-1-i;j++){//每轮的比较次数
                if(nums[j]>nums[j+1]){//前面的如果比后面的大，交换位置
                    temp = nums[j];//把大的赋给临时变量
                    nums[j]=nums[j+1];//再把小的放到刚刚存大的那个位置
                    nums[j+1]=temp;//最后把临时变量里存着的那个大的放进刚刚存小的的那个位置
                }
            }

        }
        for (int i=0;i< nums.length;i++){
            System.out.println(nums[i]);//输出所有元素
        }
    }
}

结果：