https://zhuanlan.zhihu.com/p/712393024
基本定律
全电流定律(安培环路定律)
在磁场中沿任意闭合回路磁场强度的线积分等于穿过该回路所有电流的代数和,即:
∮
H
⋅
d
l
=
∮
J
⋅
d
s
\oint H \cdot dl = \oint J \cdot ds
∮H⋅dl=∮J⋅ds
式中,电流方向与闭合回路积分方向符合右手螺旋关系时为正,反之为负。
其微分形式为:∇×H=J
对于仅存在载流导体的情况:∫H•dl=∑I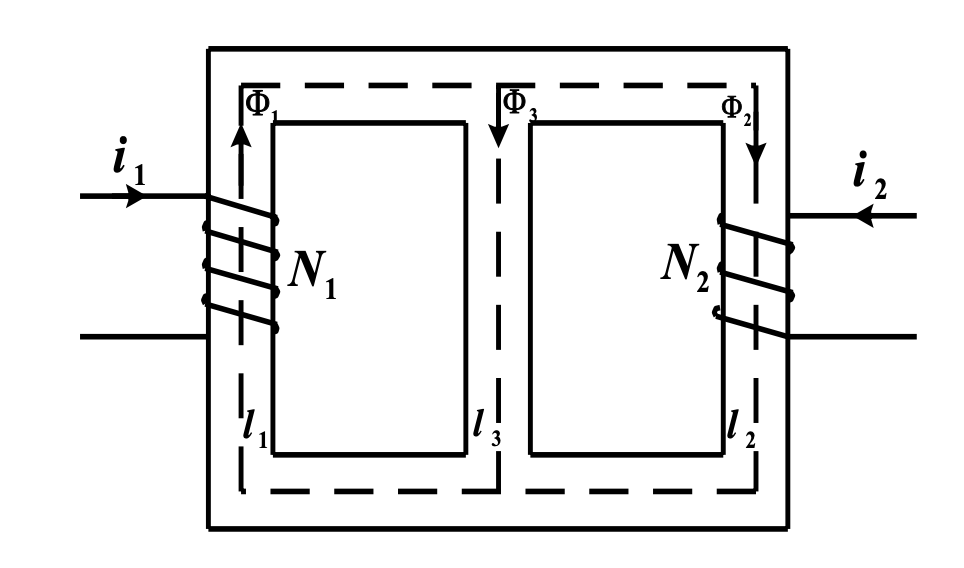
例:按图中顺时针I1、I2取回路有:
H₁l₁ + H₂l₂ = N₁i₁ - N₂i₂
按图中顺时针I1、I3取回路有:
H₁l₁ + H₃l₃ = N₁i₁
电磁感应定律
(1)线圈感应电动势——变压器电动势:
当与线圈交链的磁链Ψ随时间变化时,线圈中将感应电动势e,e的大小等于线圈所交链的磁链对时间的变化,e的方向符合楞次定律,数学描述为:
e = -dΨ/dt = -N dΦ/dt (式中N为线圈匝数)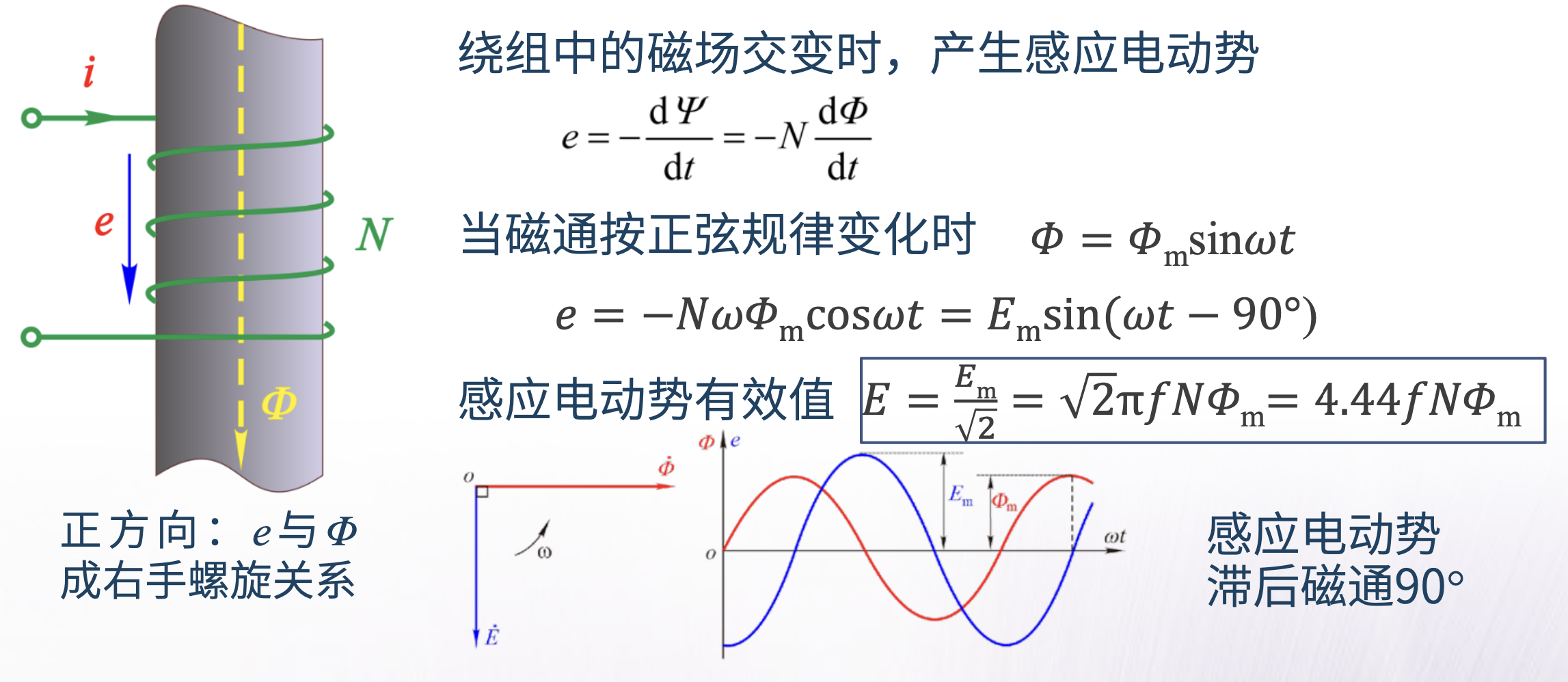
(2)运动导体感应电动势:
其数学形式为:
∇
×
E
=
−
∂
B
∂
t
导体在磁场中运动切割磁力线,产生电动势:
e
=
∫
(
v
×
B
)
⋅
d
l
若磁场均匀,导体为直段,且运动方向与磁场和导体垂直。则:
e
=
B
l
v
(方向用右手定则确定)
\text{其数学形式为:} \quad \nabla \times E = -\frac{\partial B}{\partial t} \\ \text{导体在磁场中运动切割磁力线,产生电动势:} \\ e = \int (v \times B) \cdot dl \\ \text{若磁场均匀,导体为直段,且运动方向与磁场和导体垂直。则:}\\ e = Blv \quad \text{(方向用右手定则确定)}
其数学形式为:∇×E=−∂t∂B导体在磁场中运动切割磁力线,产生电动势:e=∫(v×B)⋅dl若磁场均匀,导体为直段,且运动方向与磁场和导体垂直。则:e=Blv(方向用右手定则确定)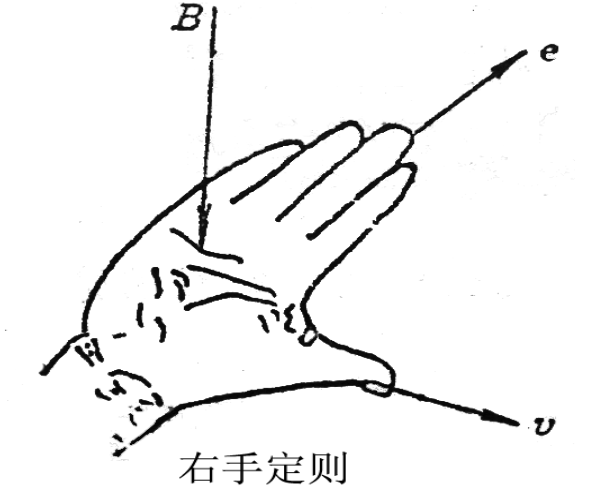

电磁力定律
载流导体在磁场中受力,大小为:
d
f
=
i
d
l
×
B
→
df = idl \times \overrightarrow{B}
df=idl×B (方向用左手定则确定)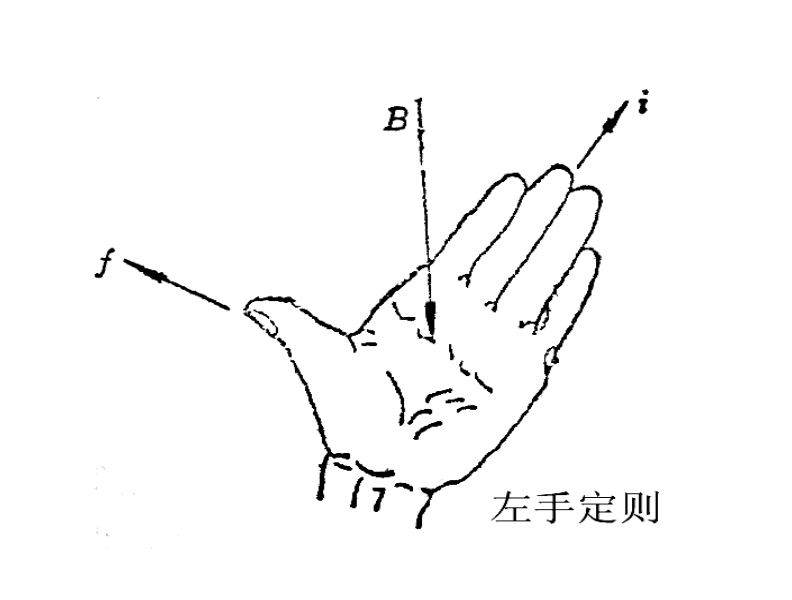
当磁场均匀,导体为直线且导体方向与磁场相垂直。则:
f
=
B
l
i
注:载流电机中,将导体
f
在电磁力
→
电磁转矩
T
e
m
f = Bli \\ 注:载流电机中,将导体f在电磁力 \rightarrow 电磁转矩Tem
f=Bli注:载流电机中,将导体f在电磁力→电磁转矩Tem
电路定律
基尔霍夫第一定律(电流定理)KCL:
∑
i
=
0
\sum i = 0
∑i=0
基尔霍夫第二定律(电压定理)KVL:
∑
u
=
∑
e
\sum u = \sum e
∑u=∑e
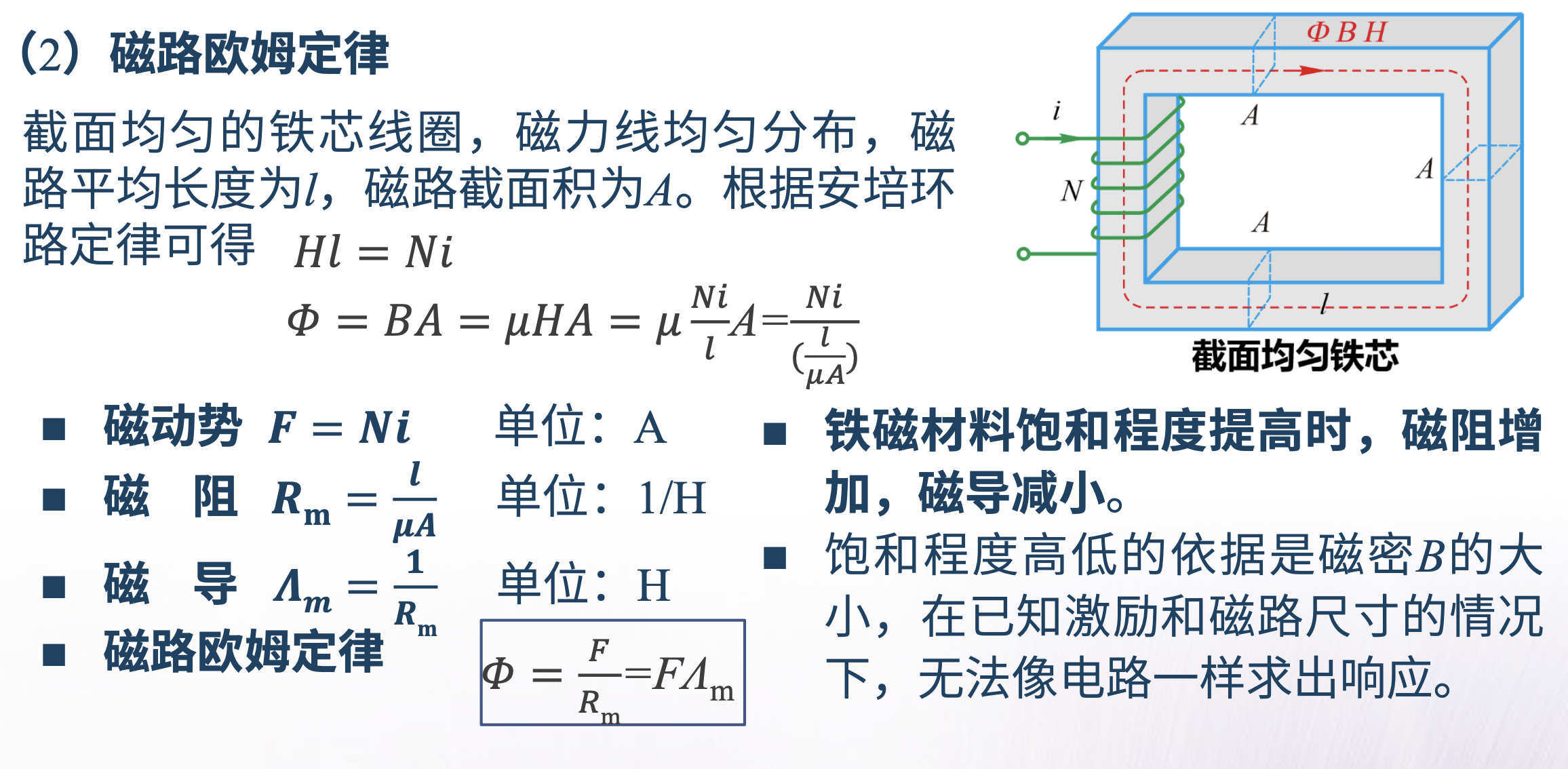
磁路欧姆定律
(1)磁路
磁场是机电能量传递的媒介,必须存在磁场
• 磁路:磁通所通过的路径.是以高导磁性材料构成的使磁通被限制在结构所确定的路径之中的一种结构(和电流在电路中被导体所限制是极为相似).
磁力线经过的路径称为磁路。磁路与电路具有相似的基本定律。无分支磁路各处磁通大小相等,磁通类比于电路中的电流。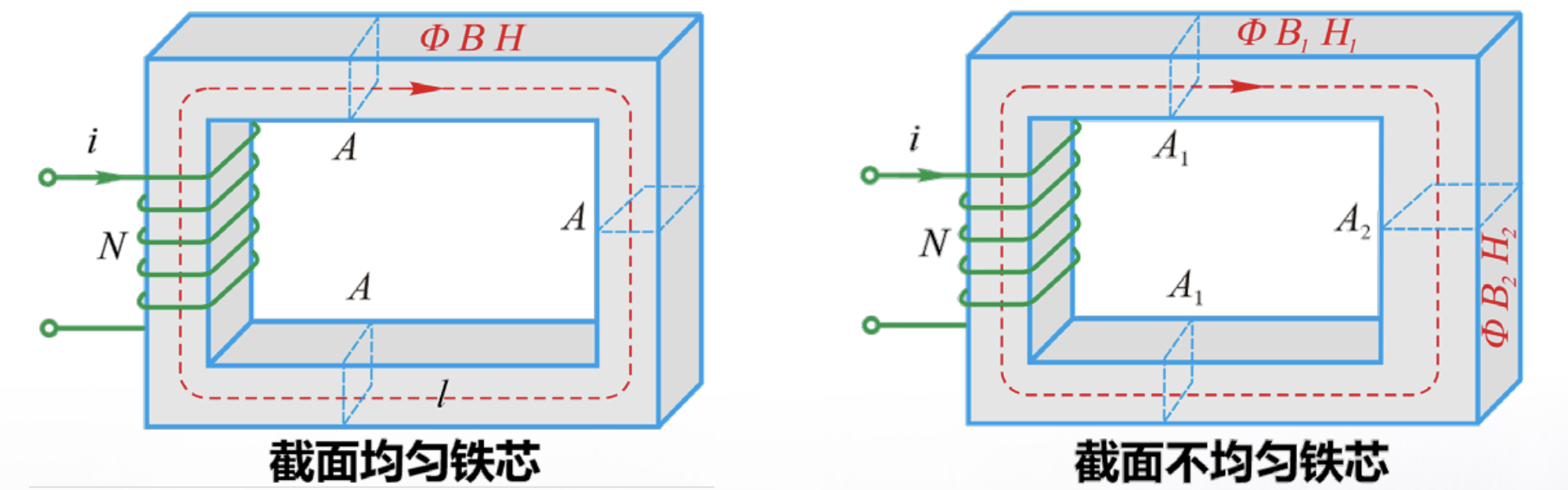
(2)磁路欧姆定律
对于等截面、磁密分布均匀、材料一致的简单磁路,假设磁通为Φ,磁动势为F=Ni,磁路截面积为A,磁路平均长度为l。
⇒
ϕ
=
∫
S
B
⋅
d
a
=
B
⋅
A
B
=
ϕ
A
H
=
F
μ
=
1
μ
⋅
ϕ
A
F
=
N
i
=
H
⋅
l
=
1
μ
⋅
l
A
⋅
ϕ
\Rightarrow \quad \phi = \int_S \mathbf{B} \cdot d\mathbf{a} = B \cdot A \\ B = \frac{\phi}{A} \\ H = \frac{F}{\mu} = \frac{1}{\mu} \cdot \frac{\phi}{A} \\ F = Ni = H \cdot l = \frac{1}{\mu} \cdot \frac{l}{A} \cdot \phi
⇒ϕ=∫SB⋅da=B⋅AB=AϕH=μF=μ1⋅AϕF=Ni=H⋅l=μ1⋅Al⋅ϕ
令:
U
m
=
H
⋅
l
U_m = H \cdot l
Um=H⋅l称为磁路的磁位降
令:
R
m
=
1
μ
⋅
l
A
R_m = \frac{1}{\mu} \cdot \frac{l}{A}
Rm=μ1⋅Al称为磁路的磁阻
磁路欧姆定理为
F
=
N
⋅
i
=
H
⋅
l
=
1
μ
⋅
l
A
⋅
ϕ
⇒
U
m
=
R
m
⋅
ϕ
F = N \cdot i = H \cdot l = \frac{1}{\mu} \cdot \frac{l}{A} \cdot \phi \\ \Rightarrow \quad U_m = R_m \cdot \phi
F=N⋅i=H⋅l=μ1⋅Al⋅ϕ⇒Um=Rm⋅ϕ
磁路基尔霍夫第一定律
磁路基尔霍夫第一定律:
- 穿过任意闭曲面的总磁通恒等于零
∮
S
B
⋅
d
s
=
∑
Φ
=
0
\oint_S \mathbf{B} \cdot d\mathbf{s} = \sum \Phi = 0
∮SB⋅ds=∑Φ=0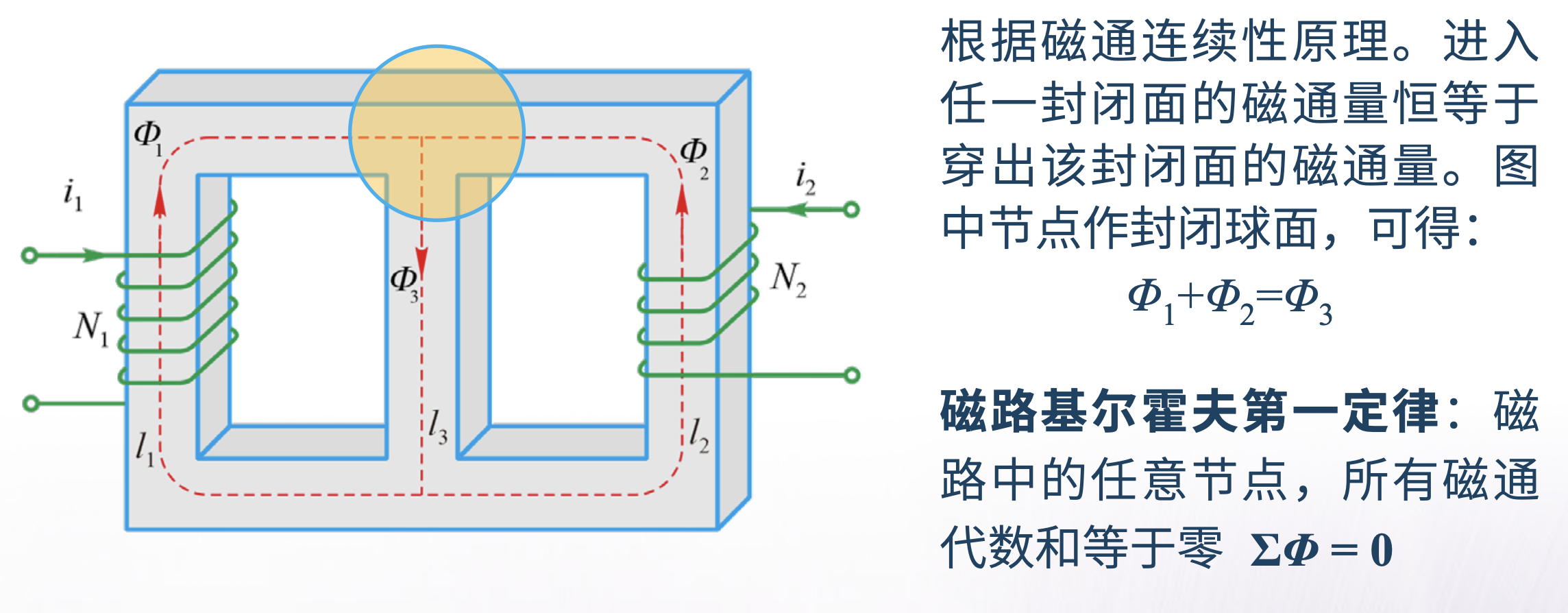
磁路基尔霍夫第二定律
沿任意闭合磁路的总磁动势恒等于各段磁路磁位降的代数和
∮
L
H
⋅
d
l
=
∮
S
J
s
⋅
d
a
\oint_L \mathbf{H} \cdot dl = \oint_S \mathbf{J_s} \cdot da
∮LH⋅dl=∮SJs⋅da
F
=
∑
i
H
i
⋅
l
i
=
∑
i
R
m
i
⋅
ϕ
m
i
=
∑
i
U
m
i
F = \sum_i H_i \cdot l_i = \sum_i R_{m_i} \cdot \phi_{m_i} = \sum_i U_{m_i}
F=∑iHi⋅li=∑iRmi⋅ϕmi=∑iUmi
F
=
N
i
=
∑
i
H
i
⋅
l
i
=
∑
i
R
m
i
⋅
ϕ
m
i
=
∑
i
U
m
i
F = Ni = \sum_i H_i \cdot l_i = \sum_i R_{m_i} \cdot \phi_{m_i} = \sum_i U_{m_i}
F=Ni=∑iHi⋅li=∑iRmi⋅ϕmi=∑iUmi
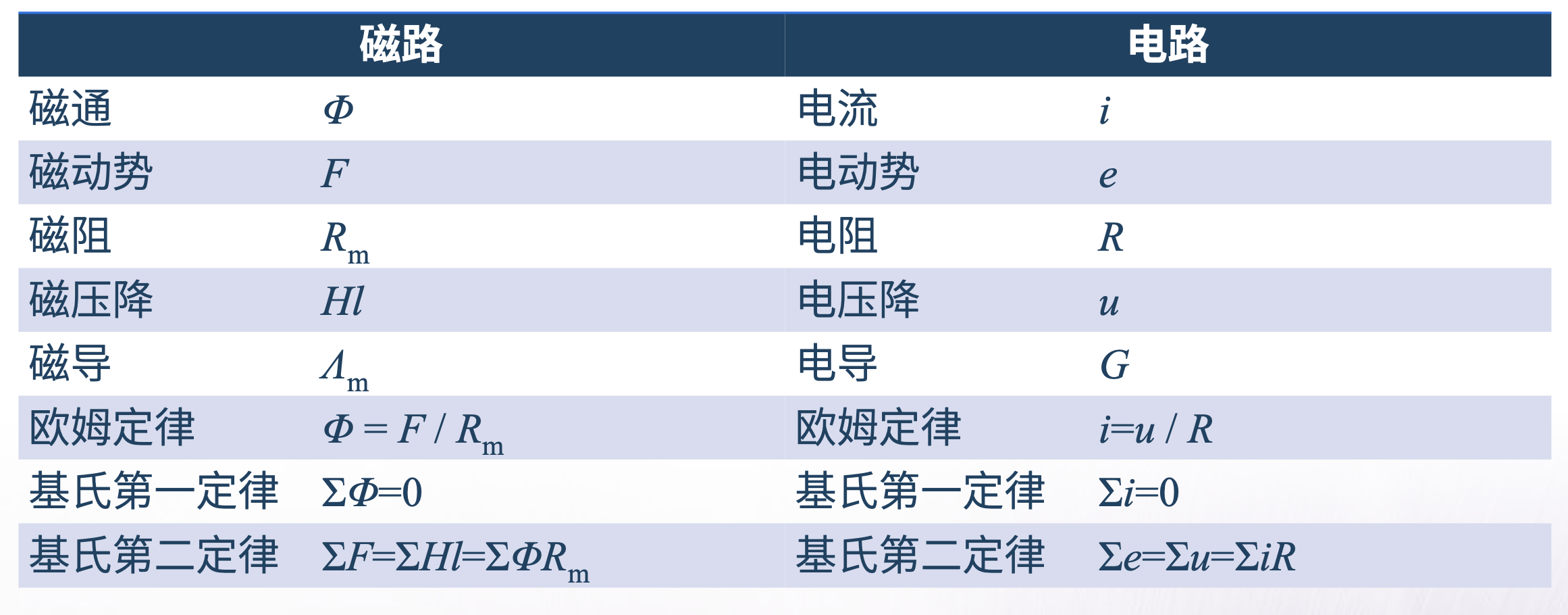
磁路和电路的比较
电机材料
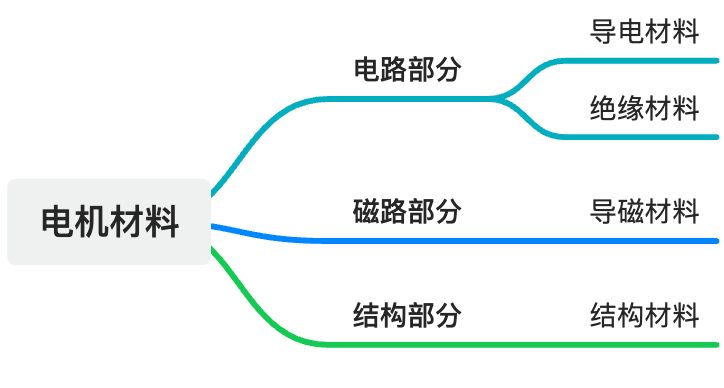
导电材料:作为电机中的电路,常采用导电性能好的材料,如紫铜或铝;
绝缘材料:作为带电体之间和铁心间的电气隔离。要求材料介电强度高而且耐热强度好;
导磁材料:作为电机中的磁路,常用硅钢片、钢板和铸钢;
结构材料:使各部分构成整体、支撑和连接其他机械。要求机械强度好、加工方便。常用铸铁、铸钢、铝合金及工程材料。
磁性材料特性
磁导率——磁密B与外加磁场强度H的比值
KaTeX parse error: {align*} can be used only in display mode.
按相对磁导率,将材料分为
顺磁物质:μ略大于1
抗磁物质:μ略小于1
铁磁物质:μ远大于1
铁磁物质包括铁、镍、钴等和他们的合金;铁磁物质在外磁场中呈现磁性大幅度增强的现象
磁滞现象
磁化曲线:磁通密度B与磁场强度H之间的关系;外磁场_H_作用下,磁密_B_随_H_变化的曲线_B_=f(H)
磁饱和:当铁磁材料中的_B_达到一定的程度后,随着_H_的增加,_B_的增加逐渐变慢,磁导率µ Fe减小。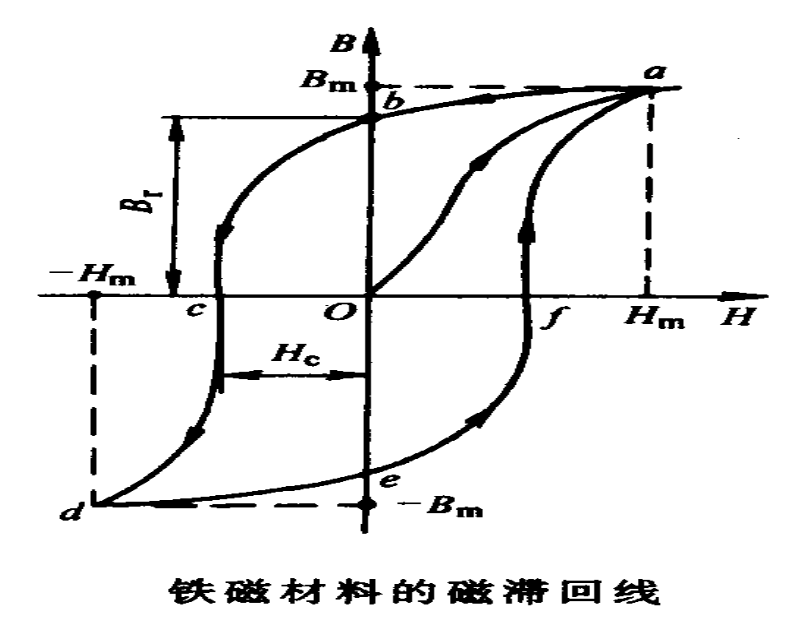
磁滞现象:铁磁材料磁化时磁通密度的变化滞后于磁场强度的变化
磁滞回线:由于磁滞效应,铁磁材料的磁化过程不可逆,在等Hmax反复磁化过程中,铁磁材料的B-H形成
的闭合曲线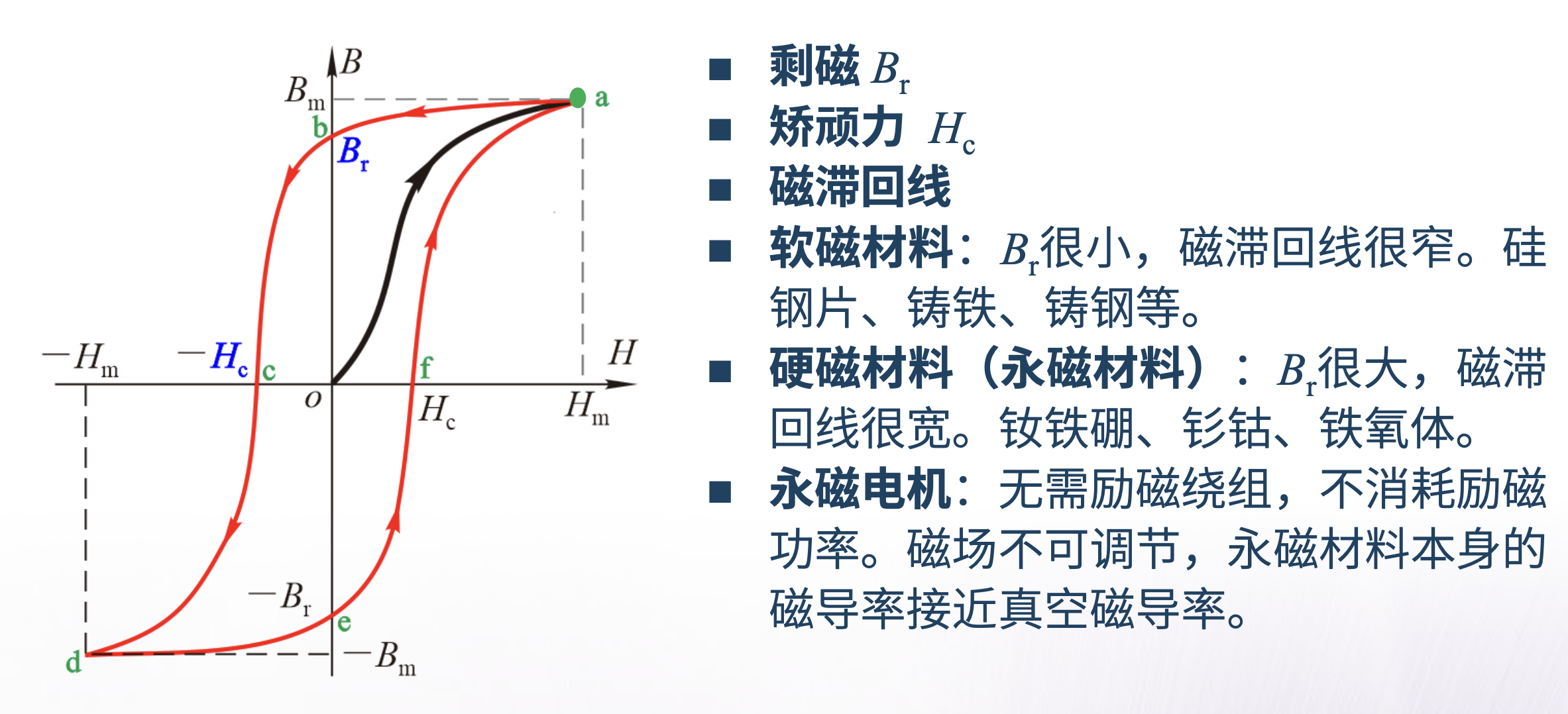
起始磁化曲线:一未磁化的铁磁材料,磁场强度H由零逐渐增大时的磁化曲线
剩磁Br:铁磁材料去掉外磁场后,铁磁材料内部仍然保留的磁通密度Br
矫顽力Hc:铁磁材料磁化后要使磁通密度由Br减小到零,需外加的反向磁场强度
磁材料分类

软磁材料
• 磁滞回线窄,剩磁Br和矫顽力Hc小
• 铸铁、钢、硅钢片等
• 软磁材料的磁导率较高
硬磁(永磁)材料
• 磁滞回线宽、Br和Hc都大的铁磁材料
• 永磁材料的性能用剩磁Br、矫顽力Hc和最大磁能积(BH)max三项指标表征
磁滞损耗
磁滞损耗:铁磁材料在交变磁场作用下反复磁化过程中,磁畴不停转动,相互摩擦,消耗的功率。从圆环铁芯线圈可推导出磁滞损耗_p_h的计算式:
p
h
=
1
T
∫
0
T
−
e
i
d
t
=
1
T
∫
0
T
(
N
d
Φ
d
t
)
(
H
l
N
)
d
t
=
1
T
∫
0
T
H
l
A
d
B
=
f
V
∮
H
d
B
p_h = \frac{1}{T} \int_{0}^{T} -eidt = \frac{1}{T} \int_{0}^{T} (N \frac{dΦ}{dt})(\frac{Hl}{N})dt = \frac{1}{T} \int_{0}^{T} HlAdB = fV ∮HdB
ph=T1∫0T−eidt=T1∫0T(NdtdΦ)(NHl)dt=T1∫0THlAdB=fV∮HdB
ph正比于磁滞回线面积、交变磁场频率f和铁芯体积V;ph工程计算经验公式
p
h
=
k
h
f
V
B
m
α
p_h = k_hfVB_m^α
ph=khfVBmα
kh——不同材料的计算系数;
α——根据材料试验确定的指数,一般1.6≤α≤2.2。
涡流与涡流损耗
涡流 (Eddy Current)
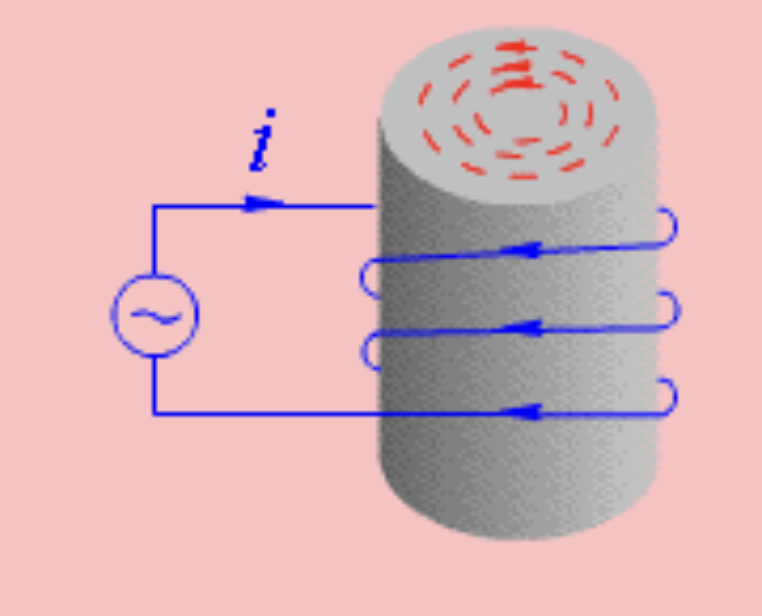
当导体置于交变的磁场中,与磁场正交的曲线中产生的感应电流,即涡流。其特点:
- 热效应 涡流是自由电子的定向运动,与传导电流有相同的热效应。
- 去磁效应 涡流产生的磁场反对原磁场的变化。
工程应用:叠片铁心(电机、变压器、电抗器等)、电磁屏蔽、电磁炉等。
涡流场分布 (Eddy Field Distribution)
以变压器铁芯叠片为例,研究涡流场分布。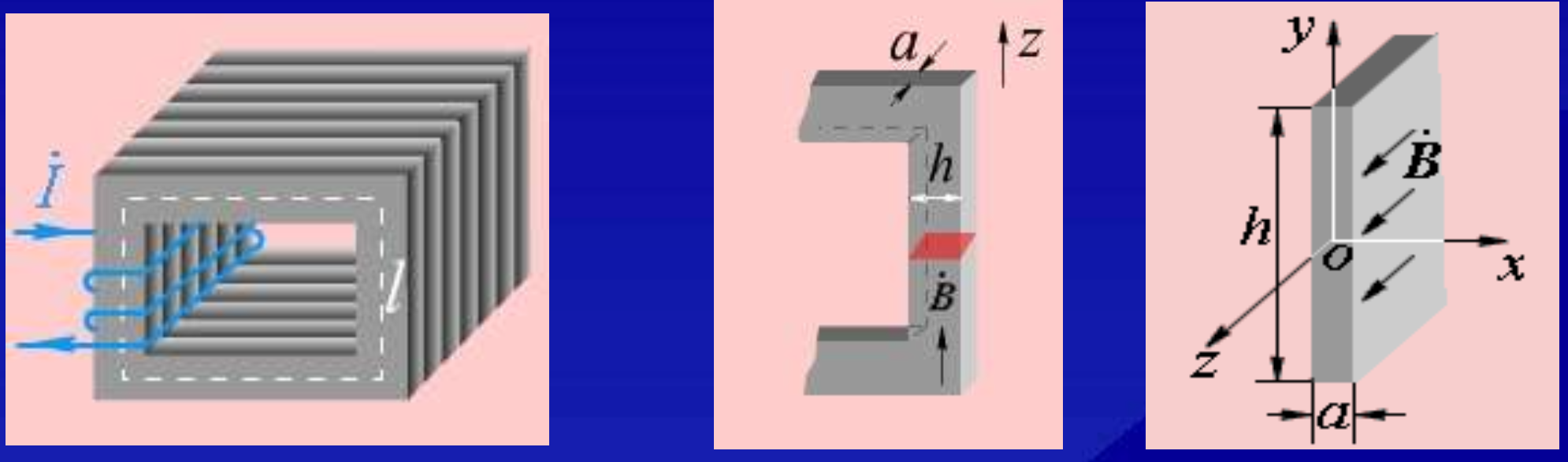
假设:
- l , h ≫ a l, h \gg a l,h≫a,场量仅是 x 的函数;
- B = B z e z B = B_z e_z B=Bzez ,故 ,故 ,故 E , J E, J E,J 分布在 x0y 平面,且仅有 y 分量;
- 磁场呈 y 轴对称,且 x = 0 x = 0 x=0 时, 时, 时, B z = B 0 B_z = B_0 Bz=B0。
在 MQS 场中,磁场满足涡流场方程(扩散方程)
∇
2
H
=
k
2
H
→
d
2
H
z
d
x
2
=
j
ω
μ
γ
H
z
=
k
2
H
z
\nabla^2 \mathbf{H} = k^2 \mathbf{H} \quad \rightarrow \quad \frac{d^2 \mathbf{H}_z}{dx^2} = j \omega \mu \gamma \mathbf{H}_z = k^2 \mathbf{H}_z
∇2H=k2H→dx2d2Hz=jωμγHz=k2Hz
解方程得到
H
z
=
B
0
ch
(
k
x
)
/
μ
B
z
=
B
0
ch
(
k
x
)
J
y
=
J
0
sh
(
k
x
)
\mathbf{H}_z = \mathbf{B}_0 \text{ch}(kx) / \mu \\ \mathbf{B}_z = \mathbf{B}_0 \text{ch}(kx) \\ \mathbf{J}_y = J_0 \text{sh}(kx)
Hz=B0ch(kx)/μBz=B0ch(kx)Jy=J0sh(kx)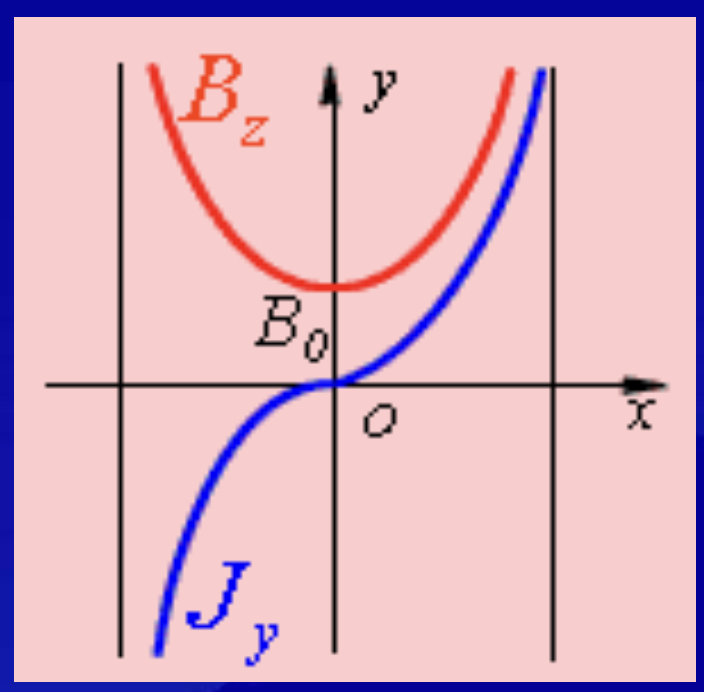
$B_z 和 J_y 的幅值分别为 \
B_z = \left| B_0 \right| \left[ \frac{1}{2} (\text{ch} 2Kx + \cos 2Kx) \right]^{\frac{1}{2}}
<
b
r
/
>
<br />
<br/>J_y = \left| J_0 \right| \left[ \frac{1}{2} (\text{ch} 2Kx - \cos 2Kx) \right]^{\frac{1}{2}}$
式中
K
=
ω
μ
γ
/
2
k
=
α
+
j
β
=
K
(
1
+
j
)
K = \sqrt{\omega \mu \gamma / 2} \quad k = \alpha + j \beta = K (1 + j)
K=ωμγ/2k=α+jβ=K(1+j)
结论:
- 去磁效应,薄板中心处磁场最小;
- 集肤效应,电流密度高对称于 y 轴,表面密度大,中心处
J
y
=
0
J_y = 0
Jy=0。
涡流损耗 (Eddy Loss)
体积V中导体损耗的平均功率为
P
e
=
∫
V
1
γ
∣
J
y
∣
2
d
V
=
B
z
a
v
2
l
h
ω
K
a
2
2
μ
s
h
K
a
−
sin
K
a
ch
K
a
−
cos
K
a
P_e = \int_V \frac{1}{\gamma} \left| \mathbf{J_y} \right|^2 dV = B_{zav}^2 lh \frac{\omega K a^2}{2 \mu} \frac{shKa-\sin Ka}{\text{ch} Ka - \cos Ka}
Pe=∫Vγ1∣Jy∣2dV=Bzav2lh2μωKa2chKa−cosKashKa−sinKa
P
e
∝
a
,
γ
,
ω
,
1
/
μ
P_e \propto a, \gamma, \omega, 1 / \mu
Pe∝a,γ,ω,1/μ,若要减少
P
e
P_e
Pe,必须减小
γ
\gamma
γ(采用硅钢),减小 a(采用叠片),提高
μ
\mu
μ(但要考虑虚磁带损耗)。研究涡流问题具有实际意义(高频涡炉、涡流的热效应、电磁屏蔽等)。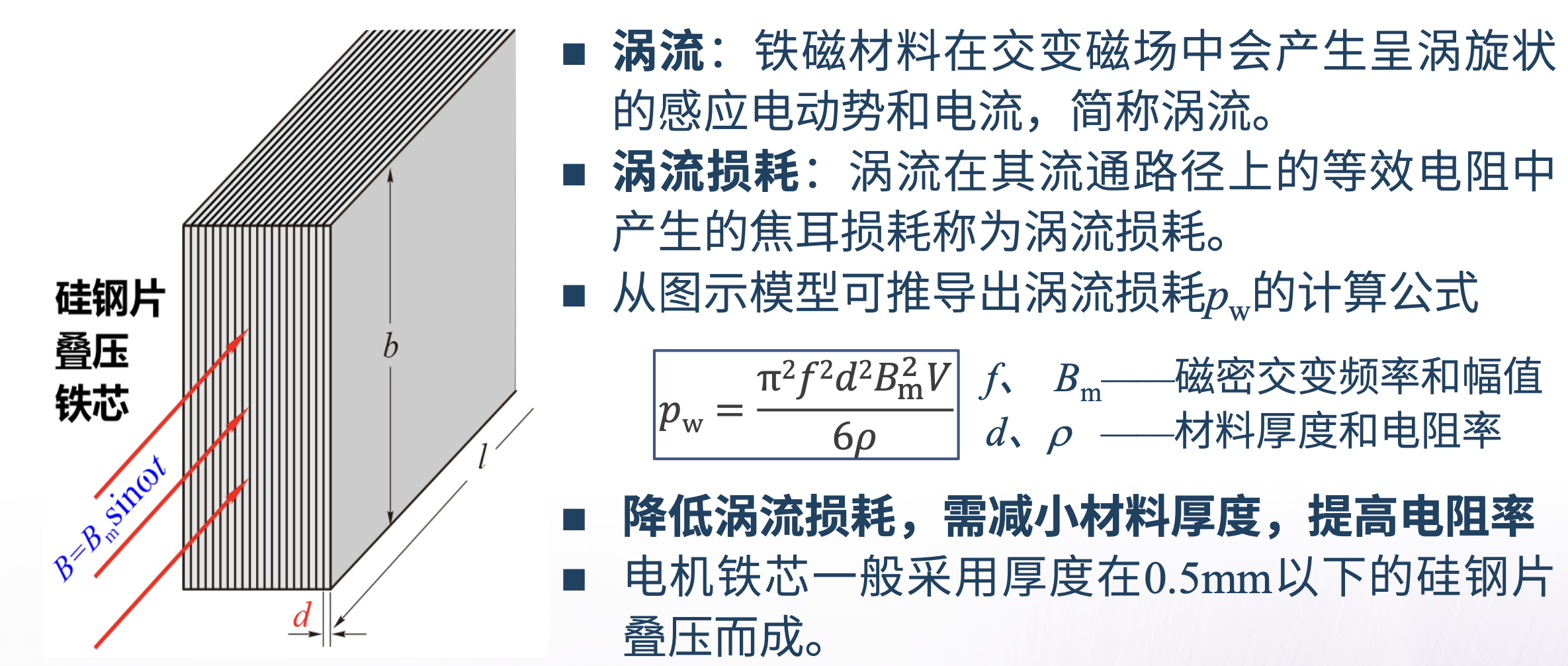
电机分析步骤
磁场中的力和力矩
电荷的洛伦兹电磁力
(1) 洛伦兹电磁力定律
处于电磁场中的电荷q所受到的电磁力F
F
=
q
(
E
+
v
×
B
)
F = q(E + v \times B)
F=q(E+v×B)
- 电磁力F(N)
- 电荷q(库仑)
- 电场强度E(V/m)
- 磁通密度B(T)
- 电荷在电磁场中的运动速度v(m/s)
纯电场中
F
=
q
E
F = qE
F=qE
- 力的方向和电场强度的方向一致
- 与电荷的运动方向无关
纯磁场中
F
=
q
(
v
×
B
)
F = q(v \times B)
F=q(v×B)
• 电场中的洛伦兹力
电磁力密度
F
v
=
ρ
(
E
+
v
×
B
)
F_v = \rho (E + v \times B)
Fv=ρ(E+v×B)
电荷密度
ρ
(
C
/
m
3
)
\rho (C/m^3)
ρ(C/m3):单位体积内的电荷
电磁力密度
F
v
(
N
/
m
3
)
F_v (N/m^3)
Fv(N/m3):单位体积内产生的电磁力
电流密度
J
=
ρ
⋅
v
J = \rho \cdot v
J=ρ⋅v
纯磁场中的电磁力密度
F
v
=
J
×
B
F_v = J \times B
Fv=J×B
• 磁场中洛伦兹力
磁性材料受力
• 详细计算十分复杂
• 需了解整个构体的磁场分布情况
简化成:只计算整体净力
• 多数机电能量转换装置采用刚性结构
• 很少要求详细计算内部应力分布
旋转电机中
• 电动机:定子磁场的旋转超前于转子磁场,定于牵引转子运动并做功
• 发电机:转子磁场超前于前于定子磁场,转子对定子做功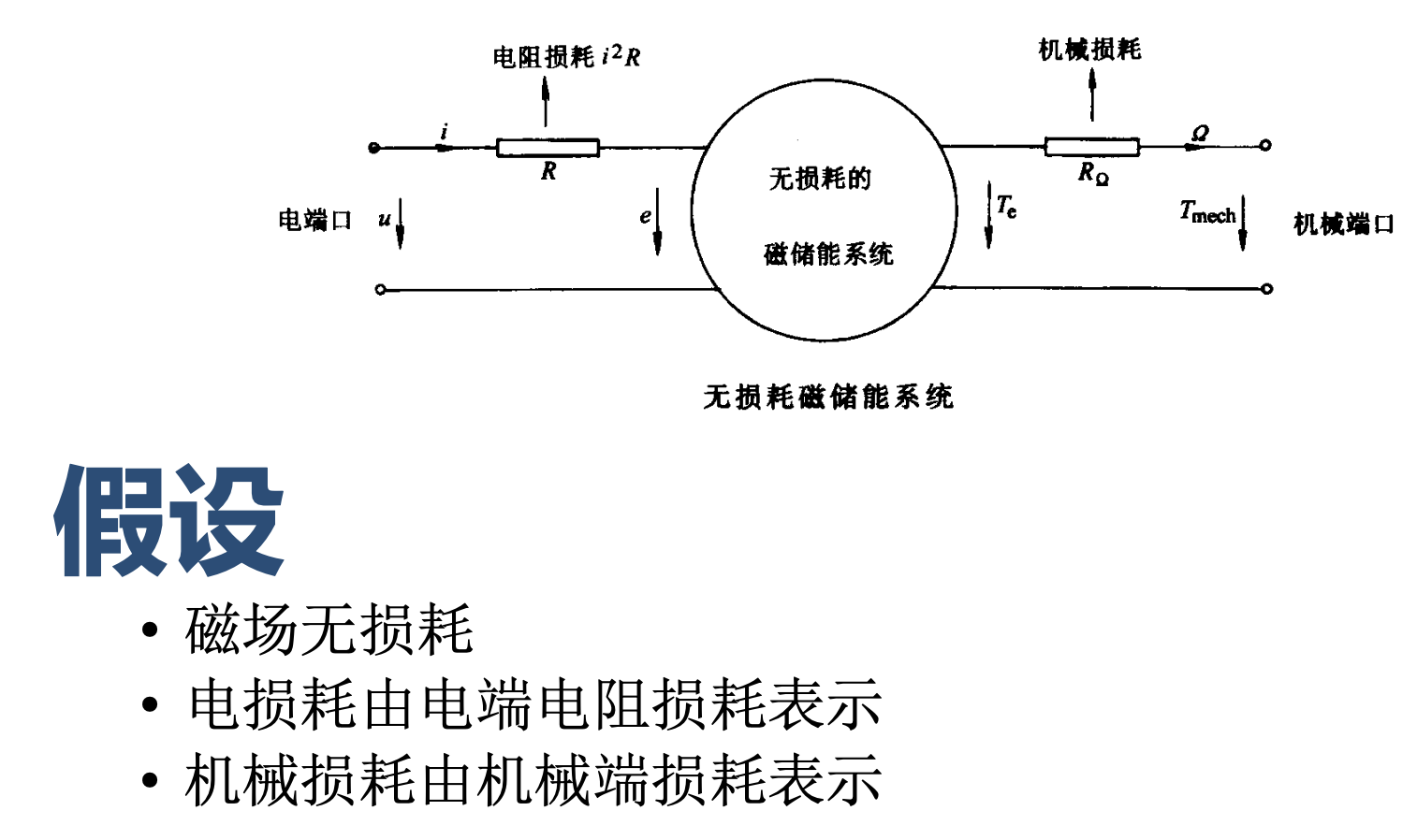
能量守恒
磁场储能
由电系统输入的电功率:
P
e
=
e
⋅
i
P_e = e \cdot i
Pe=e⋅i
磁场储能系统输出的机械功率:
d
W
f
l
d
d
t
=
P
e
−
P
m
e
c
=
e
⋅
i
−
f
f
l
d
⋅
d
x
d
t
\frac{dW_{fld}}{dt} = P_e - P_{mec} = e \cdot i - f_{fld} \cdot \frac{dx}{dt}
dtdWfld=Pe−Pmec=e⋅i−ffld⋅dtdx
单位时间磁场储能变化:
P
m
e
c
=
f
f
l
d
⋅
d
x
d
t
=
e
⋅
i
−
d
W
f
l
d
d
t
d
W
f
l
d
d
t
=
i
⋅
d
ψ
d
t
−
f
f
l
d
⋅
d
x
d
t
P_{mec} = f_{fld} \cdot \frac{dx}{dt} = e \cdot i - \frac{dW_{fld}}{dt} \\ \frac{dW_{fld}}{dt} = i \cdot \frac{d\psi}{dt} - f_{fld} \cdot \frac{dx}{dt}
Pmec=ffld⋅dtdx=e⋅i−dtdWflddtdWfld=i⋅dtdψ−ffld⋅dtdx
能量守恒:能量既不能产生也不能消亡,只能发生形式的转换
在将电能转换成机械能的系统中
电源输入 = 机械能输出 + 磁场储能的增量 + 转换为热能
d
W
e
l
e
c
=
d
W
m
e
c
+
d
W
f
l
d
+
d
W
h
e
a
t
dW_{elec} = dW_{mec} + dW_{fld} + dW_{heat}
dWelec=dWmec+dWfld+dWheat
在无损系统中
d
W
e
l
e
c
=
e
⋅
i
⋅
d
t
=
d
W
m
e
c
+
d
W
f
l
d
dW_{elec} = e \cdot i \cdot dt = dW_{mec} + dW_{fld}
dWelec=e⋅i⋅dt=dWmec+dWfld
电机分析方法
1.电机结构、实物模型分析
2.磁场分析(由空载到负载电机中磁场的建立及变化)建立电机的物理模型
3.应用基本定律,建立电机中的电动势、磁动势、功率和转矩的平衡关系,导出等值电路,建立电机的数学模型(基本方程)
4.应用基本方程分析电机的运行特性和基本控制方法
5.研究各类电机的特殊问题