在最近的研究中,实验需要结合可视化进行解释分析,于是大致上了解了下目前一些特征可视化的工具,主要分为四种类型:热力图、散点图、线性图和雷达图,并将相应的基础绘制方法做一个简单的总结。
1 热力图(Heatmap)
热力图(Heatmap)数据可视化,用于表示数据值的矩阵。它通过颜色的不同深浅来展示数据的大小或频率分布,从而使观察者能够快速识别出数据中的模式、趋势和异常。热力图通常用于表示相关性矩阵、频率分布、密度分布等。
1.1 特性
- 颜色编码:热力图使用颜色来表示数据值的大小。通常,颜色的深浅或色调变化表示数值的高低。例如,深色表示高值,浅色表示低值。常见的配色方案包括渐变色(如从蓝到红)或者单色调(如从白到黑)。
- 二维矩阵:热力图通常表示二维的数据矩阵,行和列分别对应数据的不同维度。
- 直观性:通过颜色编码,热力图能够使观察者快速了解数据的分布和趋势,特别适合于大规模数据集的初步探索和模式识别。
1.2 用途
- 相关性矩阵:展示变量之间的相关性,通常用于探索数据集中的变量关系。例如,金融数据中的股票价格相关性。
- 基因表达数据:在生物信息学中,热力图常用于表示基因表达水平。
- 密度分布:表示某个区域内数据点的密度,如地理热力图展示人口密度或事件频率。
- 频率分布:展示数据在不同区间的频率,如网站上用户点击热点图。
1.3 实例
假设有几个科技公司的股票价格数据,我们将计算这些股票之间的相关性并绘制热力图。这些公司包括:Apple 、Google 、Microsoft 、Amazon 和 Facebook。
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import yfinance as yf
# 获取股票数据
tickers = ['Apple', 'Google', 'Microsoft', 'Amazon', 'Facebook']
data = yf.download(tickers, start='2024-01-01', end='2023-8-6')['Adj Close']
# 计算每日收益率
returns = data.pct_change().dropna()
# 计算相关性矩阵
correlation_matrix = returns.corr()
# 绘制热力图
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', center=0)
plt.title('Heatmap of Stock Price Correlations')
plt.show()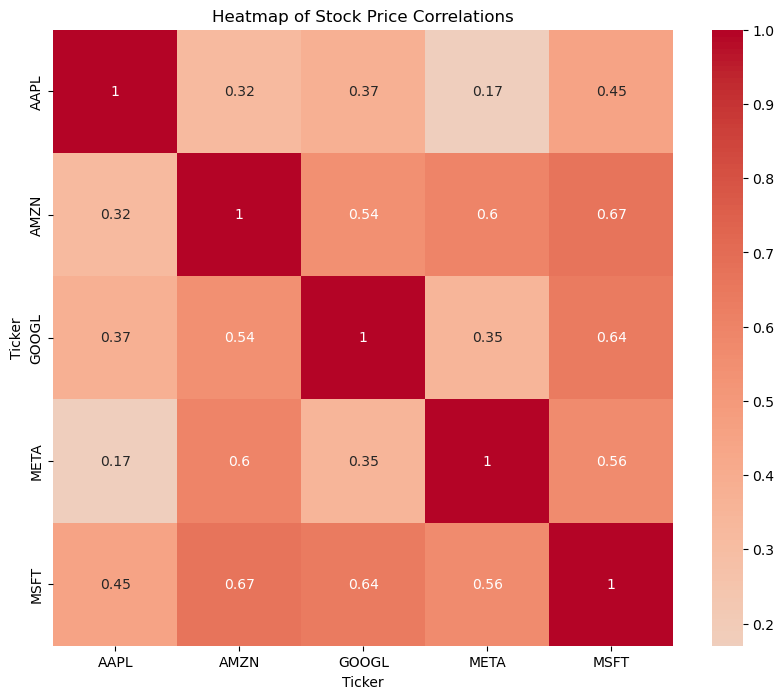
通过颜色的深浅变化,可以直观地观察到股票之间的相关关系。例如:
- 深红色表示高度正相关,表明两只股票的价格变动趋势非常相似。
- 接近白色表示相关性较弱,表明两只股票的价格变动趋势没有明显的相关性。
这种可视化方法可以帮助投资者理解不同股票之间的关系,从而优化投资组合。
2 主成分分析散点图(PCA)
主成分分析(Principal Component Analysis,PCA)是一种经典的线性降维技术,常用于数据降维、特征提取和数据可视化。PCA 通过将高维数据投影到低维空间中,保留数据中最大的方差信息,从而达到简化数据结构的目的。
2.1 特性
- 线性降维:PCA 是一种线性降维方法,通过线性变换将高维数据投影到低维空间。
- 方差最大化:PCA 寻找的是数据中方差最大的方向(主成分),这些方向能够尽可能多地保留原始数据的信息。
2.2 实例
以下是一个使用 scikit-learn 库实现 PCA 并绘制主成分分析散点图的示例代码,使用 Iris 数据集来展示 PCA 的降维效果:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 标准化数据
X = StandardScaler().fit_transform(X)
# 实现 PCA 降维
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# 可视化降维结果
plt.figure(figsize=(10, 8))
for i, target_name in enumerate(iris.target_names):
plt.scatter(X_pca[y == i, 0], X_pca[y == i, 1], label=target_name)
plt.legend()
plt.title('PCA Visualization of Iris Dataset')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.show()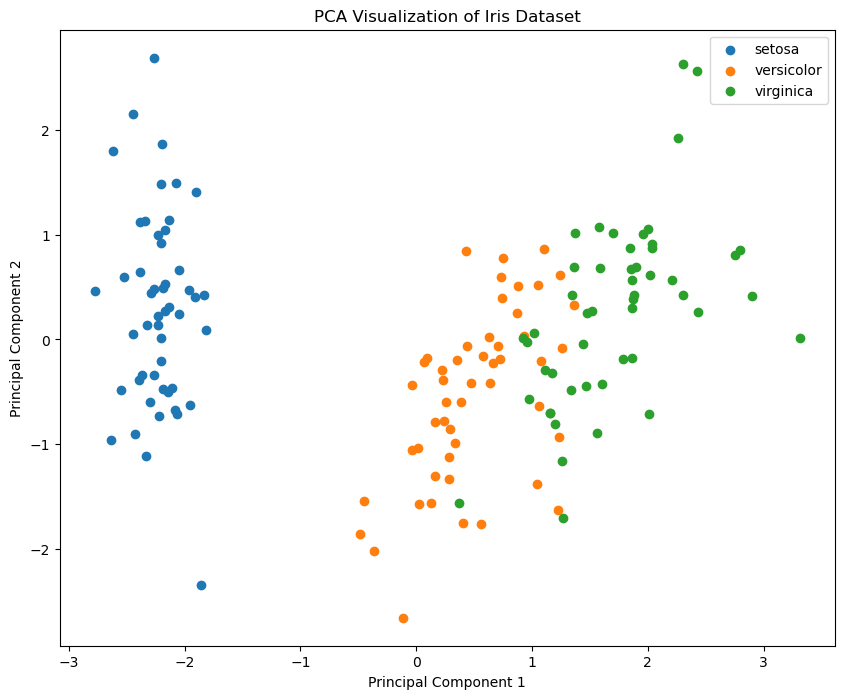
3 T-SNE 降维可视化
t-SNE(t-Distributed Stochastic Neighbor Embedding,t-分布随机邻域嵌入)是一种非线性降维技术,主要用于高维数据的可视化。它在高维数据中保留局部结构的能力特别强,能够很好地将高维数据嵌入到二维或三维空间中,便于人类观察和理解数据的分布和结构。
3.1 特性
- 保留局部结构:t-SNE 擅长保留数据的局部邻域结构,使得相似的数据点在低维空间中也靠得很近。
- 非线性降维:与线性降维方法(如 PCA)不同,t-SNE 可以很好地处理复杂的非线性关系。
- 高计算复杂度:由于 t-SNE 计算复杂度较高,适用于中小规模的数据集,大规模数据集使用时需要较长的计算时间。
3.2 实例
以下是一个使用 scikit-learn 库实现 t-SNE 的示例代码,我们使用 Iris 数据集来展示 t-SNE 的降维效果:
import numpy as np
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
# 假设特征向量矩阵为 feature_matrix
# 生成随机特征向量矩阵以供演示(实际中应替换为真实数据)
np.random.seed(42)
feature_matrix = np.random.rand(100, 512, 768)
# 对每个样本的 Token 特征向量进行平均,得到形状为 [100, 768] 的矩阵
average_features = np.mean(feature_matrix, axis=1)
# 使用 T-SNE 将形状为 [100, 768] 的矩阵降维到 2D 空间
tsne = TSNE(n_components=2, random_state=42)
reduced_features = tsne.fit_transform(average_features)
# 可视化
plt.figure(figsize=(10, 8))
plt.scatter(reduced_features[:, 0], reduced_features[:, 1], c='blue', marker='o')
plt.title('T-SNE Visualization of Reduced Features')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()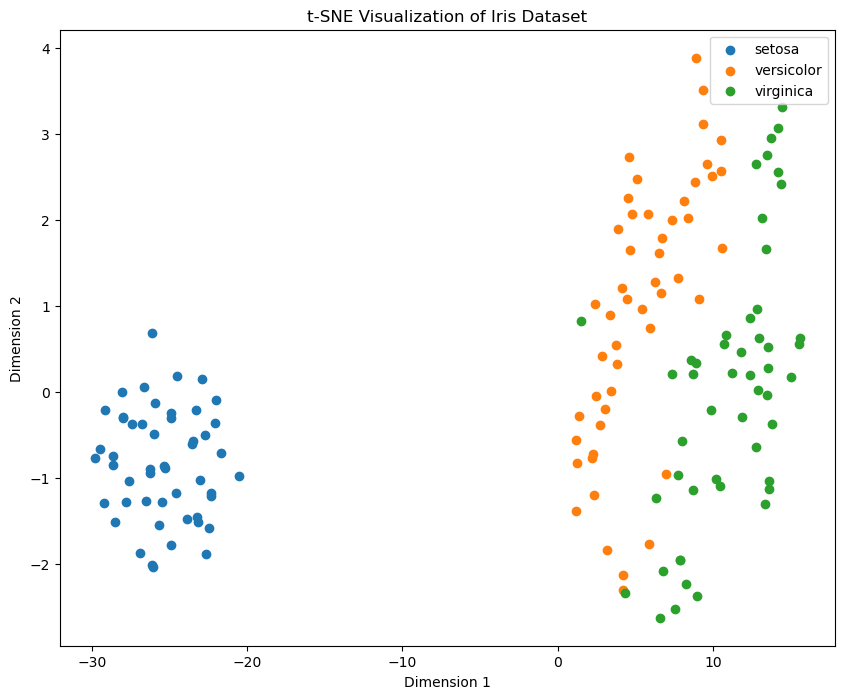
上述二维散点图展示了 Iris 数据集在 t-SNE 降维后的分布情况。不同颜色(类别)的数据点在低维空间中形成了不同的簇,表明 t-SNE 在保留数据局部结构方面的能力,这种可视化方法可以帮助我们理解高维数据的结构和模式。
4 UMAP 降维算法
UMAP(Uniform Manifold Approximation and Projection,统一流形近似与投影)是一种非线性降维技术,旨在将高维数据嵌入到低维空间中,同时保留数据的全局结构和局部结构。UMAP 在许多应用中被证明比 t-SNE 更快,并且在保留数据集结构方面表现出色。
4.1 特性
- 速度快:UMAP 通常比 t-SNE 更快,尤其是在处理大规模数据集时。
- 保留全局和局部结构:UMAP 不仅保留数据的局部邻域结构,还保留数据的全局结构。
- 参数灵活:UMAP 提供了多个参数,可以调节降维结果以适应不同的应用场景。
4.2 实例
以下是一个使用 umap-learn 库实现 UMAP 的示例代码,我们使用 Iris 数据集来展示 UMAP 的降维效果:
import numpy as np
import matplotlib.pyplot as plt
import umap
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 标准化数据
X = StandardScaler().fit_transform(X)
# 实现 UMAP 降维
umap_reducer = umap.UMAP(n_components=2, random_state=42)
X_umap = umap_reducer.fit_transform(X)
# 可视化降维结果
plt.figure(figsize=(10, 8))
for i, target_name in enumerate(iris.target_names):
plt.scatter(X_umap[y == i, 0], X_umap[y == i, 1], label=target_name)
plt.legend()
plt.title('UMAP Visualization of Iris Dataset')
plt.xlabel('Dimension 1')
plt.ylabel('Dimension 2')
plt.show()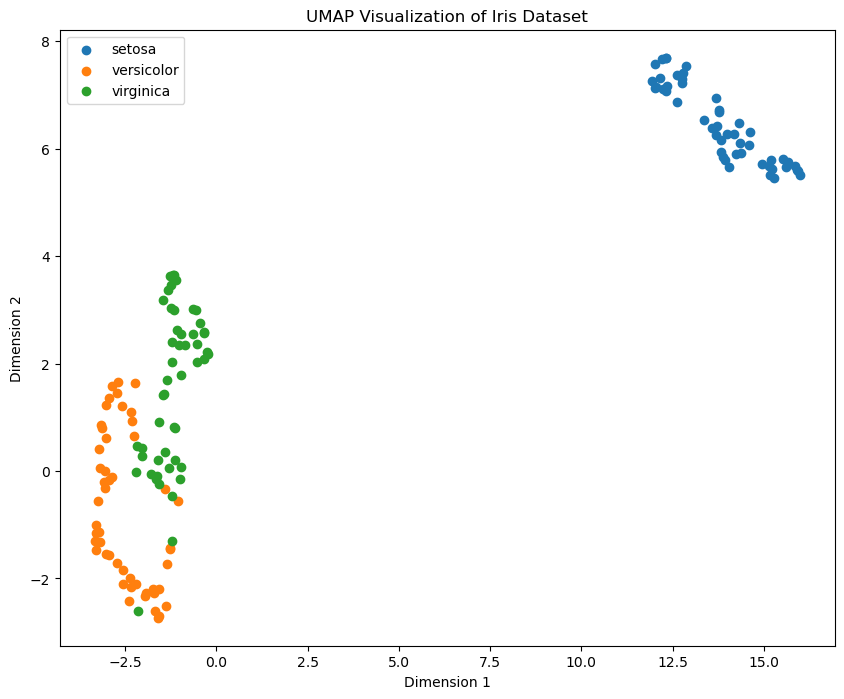
上图展示了 Iris 数据集在 UMAP 降维后的分布情况,不同类别的数据点在低维空间中形成了不同的簇,且每一个簇比 T-SNE 更加紧密,簇与簇之间的边界划分更明显,表明 UMAP 在保留数据局部和全局结构方面的能力更强。
5 自组织映射算法(SOM)
自组织映射(Self-Organizing Map,SOM)是由 Teuvo Kohonen 提出的无监督学习算法,用于将高维数据映射到低维(通常是二维)网格上,同时保留数据的拓扑结构。SOM 通过竞争学习和邻域函数来训练网络,使得相似的数据点映射到相邻的单元上,从而实现数据的可视化和聚类。
5.1 特性
- 拓扑保留:保留了高维数据的拓扑结构,相似的数据点在映射到低维空间后仍保持相邻。
- 无监督学习:是一种无监督学习算法,不需要预先标注的数据。
5.2 实例
以下是一个使用 MiniSom 库实现 SOM 的示例代码,我们同样使用 Iris 数据集来展示 SOM 的降维效果:
import numpy as np
import matplotlib.pyplot as plt
from minisom import MiniSom
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 标准化数据
X = StandardScaler().fit_transform(X)
# 初始化 SOM
som = MiniSom(x=7, y=7, input_len=4, sigma=1.0, learning_rate=0.5)
som.random_weights_init(X)
# 训练 SOM
som.train_random(X, 100)
# 可视化结果
plt.figure(figsize=(10, 8))
for i, target in enumerate(np.unique(y)):
plt.scatter(
[som.winner(x)[0] + 0.5 for x in X[y == target]],
[som.winner(x)[1] + 0.5 for x in X[y == target]],
label=iris.target_names[target]
)
plt.title('SOM Visualization of Iris Dataset')
plt.legend()
plt.show()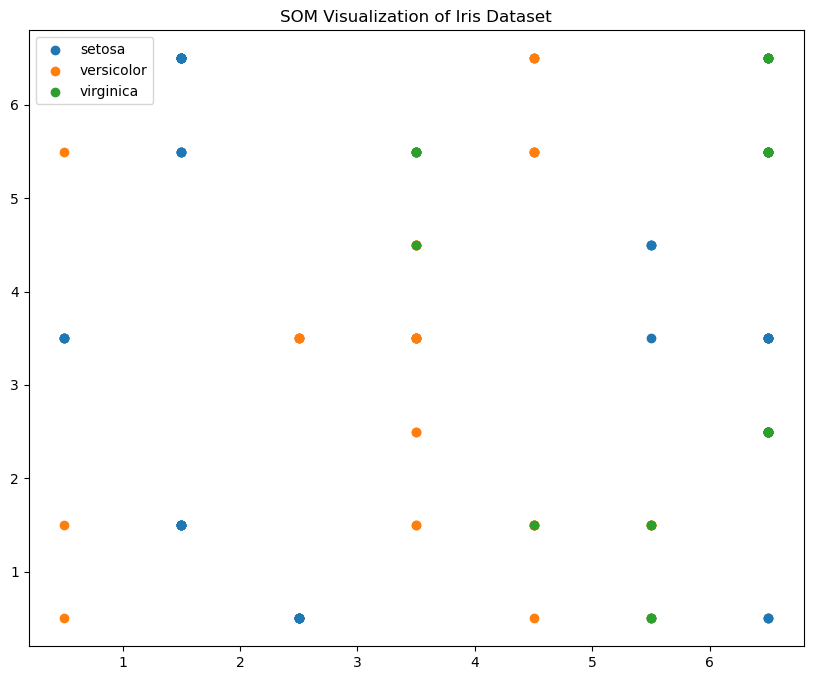
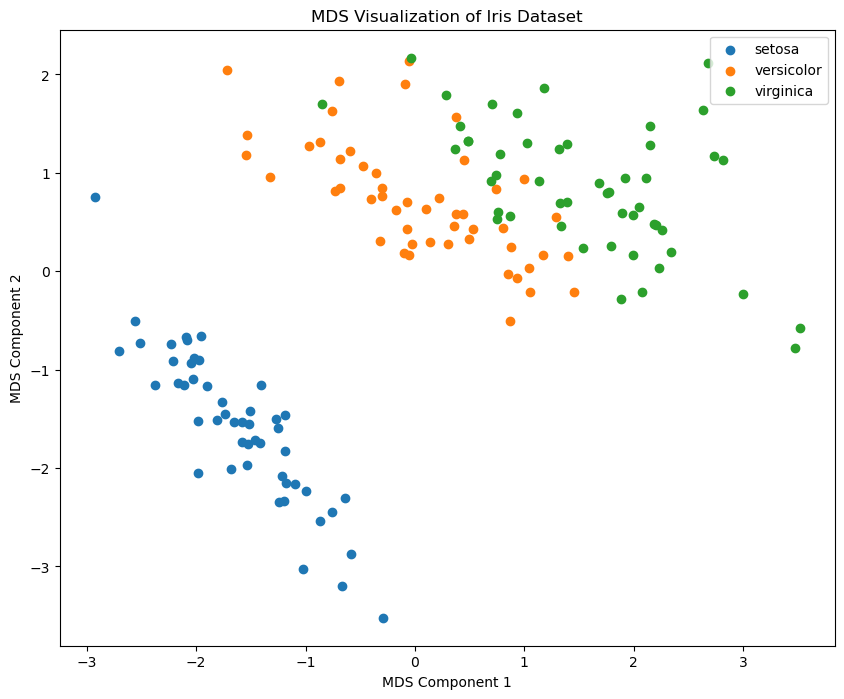
6 MDS 算法
多维尺度分析(Multidimensional Scaling,MDS)是一种统计学方法,用于将复杂、高维的相似性或距离数据转化为直观的、低维的可视化表示。MDS 最初由 Torgerson 于1952年提出,其核心思想是通过保持原始数据中对象间距离关系的近似,将数据映射到一个较低维度的空间中,使得这些对象在新空间中的位置关系能够反映出原始数据中的相似性或距离。
6.1 特性
- 保留距离关系:MDS 主要关注保留数据点之间的距离关系,而不是数据的具体坐标。
- 适用于各种距离度量:MDS 可以处理各种类型的距离度量,包括欧氏距离、曼哈顿距离等。
6.2 实例
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.manifold import MDS
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 标准化数据
X = StandardScaler().fit_transform(X)
# 实现 MDS 降维
mds = MDS(n_components=2, random_state=42)
X_mds = mds.fit_transform(X)
# 可视化降维结果
plt.figure(figsize=(10, 8))
for i, target_name in enumerate(iris.target_names):
plt.scatter(X_mds[y == i, 0], X_mds[y == i, 1], label=target_name)
plt.legend()
plt.title('MDS Visualization of Iris Dataset')
plt.xlabel('MDS Component 1')
plt.ylabel('MDS Component 2')
plt.show()7 Isomap 算法
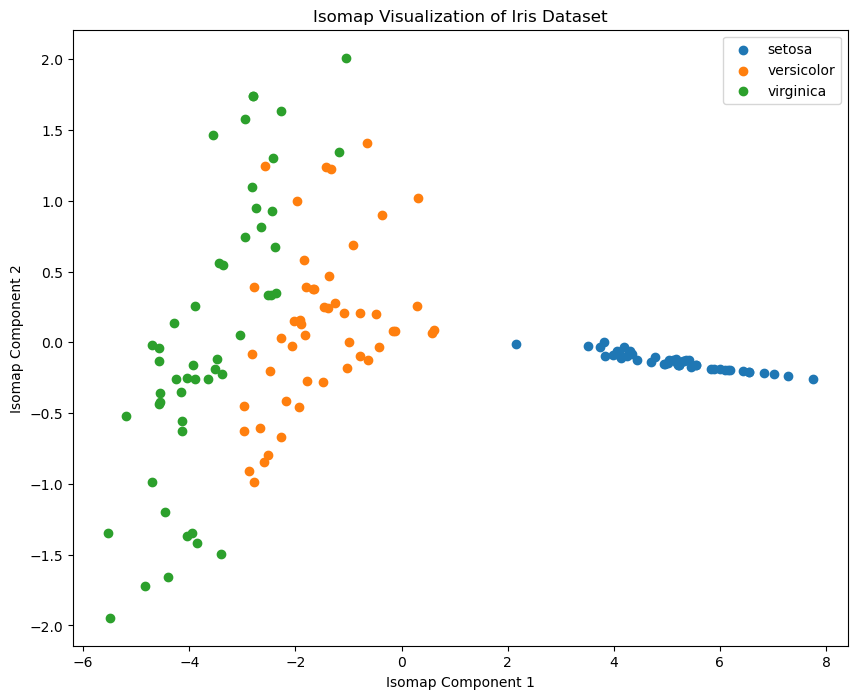
Isomap(Isometric Mapping)是一种非线性降维方法,旨在保留数据在高维空间中的几何距离结构,同时将其嵌入到低维空间中,Isomap 是多维尺度分析(MDS)的扩展,主要通过测量数据点在流形上的地质距离(即距离图上的最短路径)来实现这一目标。
7.1 特性
- 保留流形结构:Isomap 通过保留数据点在流形上的几何距离,能够更好地揭示数据的内在结构。
- 全局优化:Isomap 通过全局优化方法,将高维数据点嵌入到低维空间中。
- 适用于非线性数据:相比于线性降维方法(如 PCA),Isomap 更适用于包含非线性结构的数据集。
7.2 实例
以下是一个使用 scikit-learn 库实现 Isomap 的示例代码,我们同样使用 Iris 数据集来展示 Isomap 的降维效果:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.manifold import Isomap
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 标准化数据
X = StandardScaler().fit_transform(X)
# 实现 Isomap 降维
isomap = Isomap(n_components=2, n_neighbors=5)
X_isomap = isomap.fit_transform(X)
# 可视化降维结果
plt.figure(figsize=(10, 8))
for i, target_name in enumerate(iris.target_names):
plt.scatter(X_isomap[y == i, 0], X_isomap[y == i, 1], label=target_name)
plt.legend()
plt.title('Isomap Visualization of Iris Dataset')
plt.xlabel('Isomap Component 1')
plt.ylabel('Isomap Component 2')
plt.show()8 平行坐标图(Parallel Coordinates Plot)
平行坐标图(Parallel Coordinates Plot)是一种数据可视化技术,常用于多变量数据的可视化,它可以帮助我们在二维平面上展示高维数据,揭示不同变量之间的关系和模式。
8.1 特性
- 高维数据可视化:平行坐标图特别适用于可视化高维数据,每个数据点通过在平行坐标轴上的连接线表示。
- 变量间关系:能够直观地展示多个变量之间的关系和相互影响。
- 异常检测:可以通过观察图形中异常的模式或线条,识别数据中的异常点。
8.2 原理
在平行坐标图中,每个变量对应一条垂直的坐标轴,数据集中每个观测值在各个坐标轴上都有一个点,这些点通过线段连接起来,形成一条折线,通过观察这些折线的形状和交叉情况,可以分析变量之间的关系和数据的分布情况。
8.3 实例
以下是一个使用 matplotlib 库绘制平行坐标图的示例代码,我们同样使用 Iris 数据集来展示平行坐标图的效果:
import pandas as pd
import matplotlib.pyplot as plt
from pandas.plotting import parallel_coordinates
from sklearn.datasets import load_iris
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 创建 DataFrame
df = pd.DataFrame(X, columns=iris.feature_names)
df['target'] = y
# 绘制平行坐标图
plt.figure(figsize=(10, 8))
parallel_coordinates(df, 'target', color=('#556270', '#4ECDC4', '#C7F464'))
plt.title('Parallel Coordinates Plot of Iris Dataset')
plt.xlabel('Features')
plt.ylabel('Value')
plt.show()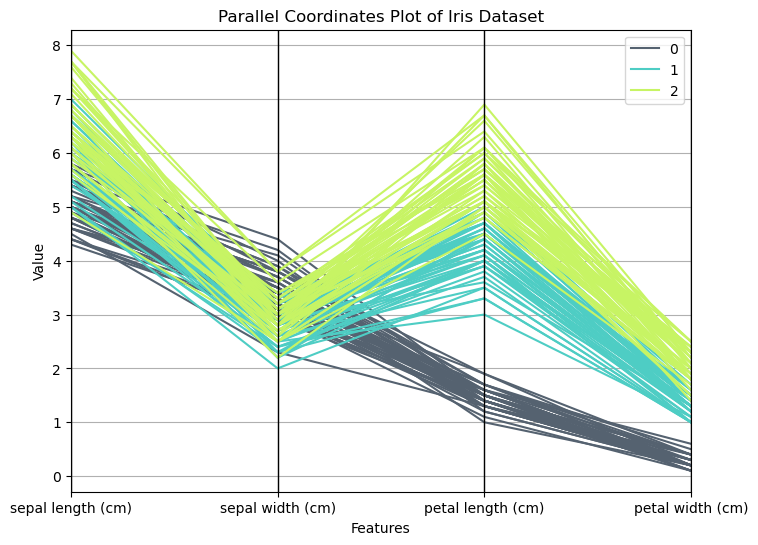
平行坐标图广泛应用于以下领域:
- 多变量数据分析:帮助分析和理解多变量数据集的内在结构和关系。
- 模式识别:用于识别数据中的模式、趋势和异常点。
- 分类和聚类:在机器学习中用于探索和理解分类和聚类结果。
9 雷达图(Radar Chart)
雷达图(Radar Chart),也称为蜘蛛网图(Spider Chart)或星形图(Star Plot),是一种用于显示多变量数据的图表,它能够在二维平面上展示多个变量的值和相互关系,常用于比较数据集的不同特征值。
9.1 特性
- 多变量展示:雷达图特别适用于展示和比较多维数据,每个变量对应一个轴,从中心点向外辐射。
- 直观对比:能够直观地对比多个数据集在各个变量上的表现。
- 易于理解:通过图形的形状和面积,可以快速识别数据的特征和模式。
9.2 实例
以下是一个使用 matplotlib 库绘制雷达图的示例代码,我们使用一个示例数据集来展示如何绘制雷达图:
import numpy as np
import matplotlib.pyplot as plt
# 定义数据
labels = ['A', 'B', 'C', 'D', 'E']
num_vars = len(labels)
# 示例数据
data1 = [4, 3, 2, 5, 4]
data2 = [3, 4, 5, 2, 3]
data3 = [5, 2, 3, 4, 5]
# 添加一个闭合点
data1 += data1[:1]
data2 += data2[:1]
data3 += data3[:1]
# 计算角度
angles = np.linspace(0, 2 * np.pi, num_vars, endpoint=False).tolist()
angles += angles[:1]
# 初始化雷达图
fig, ax = plt.subplots(figsize=(10, 8), subplot_kw=dict(polar=True))
# 绘制第一个数据集
ax.plot(angles, data1, linewidth=1, linestyle='solid', label='Dataset 1')
ax.fill(angles, data1, alpha=0.25)
# 绘制第二个数据集
ax.plot(angles, data2, linewidth=1, linestyle='solid', label='Dataset 2')
ax.fill(angles, data2, alpha=0.25)
# 绘制第三个数据集
ax.plot(angles, data3, linewidth=1, linestyle='solid', label='Dataset 3')
ax.fill(angles, data3, alpha=0.25)
# 添加标签
ax.set_xticks(angles[:-1])
ax.set_xticklabels(labels)
# 添加图例
ax.legend(loc='upper right', bbox_to_anchor=(0.1, 0.1))
# 显示雷达图
plt.title('Radar Chart Example')
plt.show()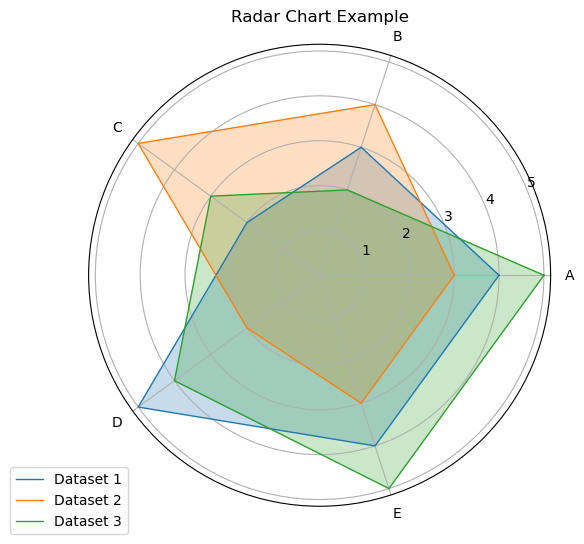
雷达图的每个轴代表一个变量,这些轴从中心点开始向外辐射。数据点在每个轴上的位置表示该变量的值,所有数据点用线连接起来形成一个多边形,多个数据集可以通过不同颜色的多边形进行比较。上图展示了三个数据集在五个变量上的表现,不同数据集的多边形形状和面积可以帮助我们快速比较它们在各个变量上的表现。
雷达图广泛应用于以下领域:
- 性能评估:用于评估和比较产品或系统在多个指标上的性能。
- 市场分析:用于展示和比较不同市场或产品的特征和优势。
- 个人技能评估:用于展示和比较个人在多个技能或能力上的表现