题目：

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

思路：

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环 完成了一个不断搜索区间的过程。

本题可以使用滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

那么滑动窗口如何用一个for循环来完成这个操作呢。

首先要思考 如果用一个for循环，那么应该表示 滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示 滑动窗口的起始位置，那么如何遍历剩下的终止位置？

此时难免再次陷入 暴力解法的怪圈。

所以 只用一个for循环，那么这个循环的索引，一定是表示 滑动窗口的终止位置。

窗口就是 满足其和 ≥ s 的长度最小的 连续 子数组。

窗口的起始位置如何移动：如果当前窗口的值大于等于s了，窗口就要向前移动了（也就是该缩小了）。

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

解题的关键在于 窗口的起始位置如何移动，如图所示：

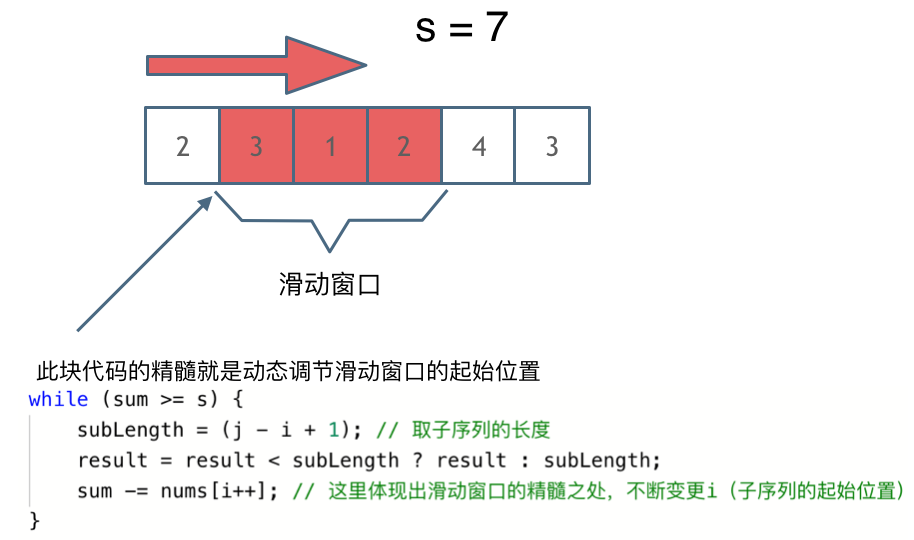
可以发现滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        //双指针-滑动窗口思想
        //两个指针指向所求的连续子数组的两侧
        //起始左右指针都指向nums[0],定义sum记录集合中的数值和，定义length记录连续子数组的最小长度
        //右指针不断右移，并且更新连续子数组的数值和sum
        // 若sum >= target,则将左指针不断右移并且sum中减去nums[left],直至sum < target.并且判断并更新length
        // 若sum < target,则继续右移左指针直到sum >= target.
        
        int sum = 0,length = 0x3f3f3f3f;
        int subL = 0;//记录每个数值和 >= target 的连续子数组长度，用于与length比较取最小
        
        for (int left = 0,right = 0; right < nums.length; right++) {
            sum += nums[right];
            while (sum >= target){
                sum -= nums[left];
                subL =right - left + 1;
                //length与当前数组长度比较取最小
                length = Math.min(length, subL);
                left++;
            }
        }
        
        //有可能整个数组之和相加都 < target，这种情况没有进入while循环进行比较赋值，此处进行三元判断
        return length == 0x3f3f3f3f ? 0 : length;
    }
}