时间序列分析基础20问

时间序列分析是一类特殊的数据分析问题。它是对连续间隔离散时间序列的观察。在现实世界中的应用包括天气预测模型、股市预测等。

本文通过20个问题，深入解析时间序列分析的基础概念和方法。

1. 什么是时间序列数据？

时间序列数据是按照时间顺序排列的、在等间隔时间点上收集或记录的一系列数据点。例如，日常股票价格、每小时温度记录、每月销售数据等都属于时间序列数据。

2. 什么是时间序列分析？

时间序列分析是一种统计方法，用于分析和解释在连续、等间隔时间点收集或记录的数据点。通过识别数据中的模式、趋势和关系，时间序列分析可以用来预测或预估未来值。

3. 时间序列数据有哪些常见组成部分？

趋势（Trend）：长期的上升或下降方向，反映数据的总体变化。
季节性（Seasonality）：在固定时间间隔内重复出现的周期性模式，与季节、月份等相关。
周期性（Cyclicality）：较长时间间隔内的波动模式，没有固定周期，通常与经济或业务周期相关。
不规则波动（Irregular Fluctuations or Noise）：无法用趋势、季节性或周期性解释的随机变化，通常被视为噪声。

4. 什么是时间序列的趋势（Trend）？

趋势是指时间序列数据中长期的上升或下降的运动方向。它反映了数据随时间的总体变化趋势，而不考虑短期波动。比如某公司销售额的长期增长趋势，或某城市人口的长期增长。

处理时间序列数据中的趋势涉及使用去除趋势的方法。两种常见的方法是移动平均（如简单移动平均（SMA）或指数移动平均（EMA）），它们平滑短期波动；和差分法，通过计算相邻观测值之间的差异来消除趋势。

5. 什么是季节性（Seasonality）？

季节性是指时间序列数据中在特定时间间隔内重复出现的模式或规律。季节性通常与时间的某些特定点相关联，如季节、月份或星期。比如零售业在节假日销售高峰、气温的年周期变化。

检测季节性可通过可视化检查或统计方法（如自相关函数）进行，模式表现为定期的峰值或谷值。处理季节性的方法包括季节差分、移动平均或高级方法（如季节性分解（STL））。使用 SARIMA 或季节回归等建模方法可以考虑季节性，确保更准确的预测和分析，从而揭示底层趋势和模式。

6. 什么是周期性（Cyclicality）？

周期性是指时间序列数据中在较长时间间隔内出现的波动模式。与季节性不同，周期性没有固定的时间间隔，通常与经济或业务周期有关，例如经济衰退和复苏周期、业务中的扩张和收缩周期。

7. 什么是白噪声（White Noise）？

白噪声是指时间序列中的每一个观测值都是彼此独立的随机变量，且具有相同的分布（通常是均值为零，方差为常数的正态分布）。白噪声没有自相关性，所有滞后期的自相关系数应接近于零。例如，突发的自然灾害对销售数据的影响、市场上的突发事件或突发新闻。

在时间序列建模中，白噪声通常被视为数据中不可解释的随机成分。它常用于检验模型的拟合优度，例如通过检查模型残差是否符合白噪声的特性来评估模型的有效性。

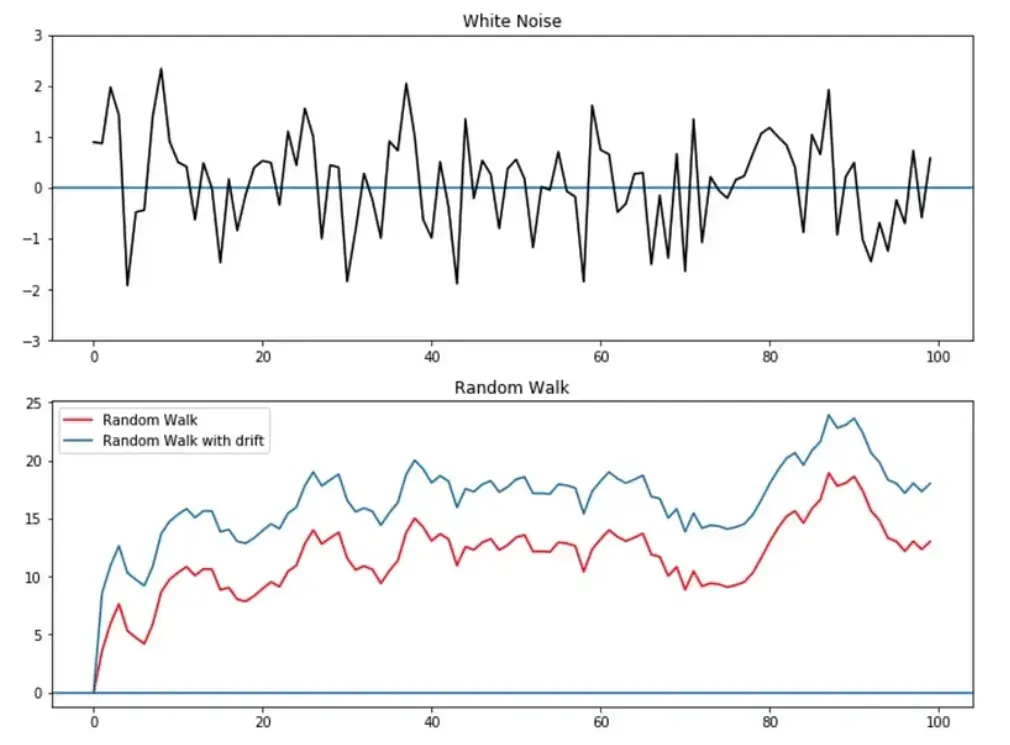
8. 什么是随机游走（Random Walk）？

随机游走是一种特定类型的时间序列过程。随机游走序列具有趋势性，即每个观测值的变化取决于前一个观测值和一个随机噪声项。它的均值和方差会随时间变化，因此是不平稳的。

随机游走模型常用于金融数据和经济数据的建模，例如股票价格的模型。在建模和预测时，识别数据是否符合随机游走是很重要的，因为这会影响选择的模型和预测的方法。

9. 什么是残差（Residuals）？

残差是指时间序列数据中实际观测值与模型预测值之间的差异。假设你使用一个模型预测时间序列数据，那么残差就是实际观测值减去预测值的结果。

残差用于诊断模型的拟合效果和进一步改进模型。通过检查残差是否符合白噪声特性，分析师可以判断模型是否适合数据。

10. 什么是时间序列分析中的平稳性概念？

时间序列的平稳性意味着其统计特性（如均值和方差）保持不变。它很重要，因为许多模型在处理平稳数据时效果最佳，这简化了模式识别，从而实现准确预测和可靠推断。非平稳数据可能会误导分析，因此确保平稳性对于保证时间序列模型的有效性至关重要。

11. 解释时间序列分析中的假设检验。你通常会进行哪些检验？

假设检验用于评估时间序列数据中的假设。常见的检验包括：

ADF 检验： 检查数据的平稳性。
KPSS 检验： 检查数据的趋势平稳性。
白噪声检验： 检查序列随机性。
格兰杰因果检验： 确定一个时间序列是否可以预测另一个。
这些检验帮助确保数据和模型的有效性，从而提高预测的准确性。

12. 解释时间序列分析中的滞后概念。

在时间序列分析中，滞后（Lag） 是指时间序列数据中一个观测值相对于另一个观测值的时间间隔。简单来说，滞后表示的是时间上的距离或延迟。

例子：假设我们有一个时间序列数据记录了某产品的月度销售额 [100, 120, 130, 150, 140]。如果我们讨论“滞后1期”，就意味着我们关注的是当前月份的销售额与前一个月（即滞后1期）的销售额之间的关系。例如，2023年3月的销售额与2023年2月的销售额之间的滞后关系。

13. 什么是自相关（Autocorrelation）？

自相关（Autocorrelation）是指时间序列中一个观测值与其自身滞后值之间的相关性。它衡量了时间序列数据在不同时间点之间的依赖关系和规律性。简单来说，自相关检验的是一个时间点的数据与之前某个时间点数据的相关程度，帮助识别数据中的周期性和模式。

14. 什么是偏自相关（Partial Autocorrelation）？

偏自相关（Partial Autocorrelation）是指在去除中间观察值影响后的时间序列数据与其滞后值之间的相关性。它衡量了一个滞后值对当前值的直接影响，而不受其他滞后值的干扰。偏自相关函数（PACF）帮助识别在多大程度上一个特定的滞后期直接影响当前值，对于确定时间序列模型的阶数尤其重要。

15. 时间序列有哪些常用的模型？

常见的时间序列模型包括

自回归模型(AR): 预测当前值是过去值的线性组合
移动平均模型(MA): 预测当前值是过去误差项的线性组合。
自回归移动平均模型(ARMA): 结合了自回归和移动平均的模型来预测时间序列。
差分自回归移动平均模型(ARIMA): 通过差分操作将非平稳时间序列转换为平稳序列后再进行ARMA建模，用于建模和预测线性时间序列数据
SARIMA(季节性ARIMA): 扩展了ARIMA以处理季节性成分；
向量自回归模型 (VAR): 用于多变量时间序列，每个变量依赖于自身和其他变量的过去值，适用于研究和预测多个相互影响的时间序列，如经济指标、股票价格等。
指数平滑模型 (Exponential Smoothing Models): 通过指数加权移动平均来平滑和预测时间序列；

此外，还有许多更复杂的模型，如状态空间模型、机器学习模型（如随机森林和梯度提升机）和深度学习模型（如RNN和LSTM），这些模型适用于处理非线性和复杂的时间序列数据。

16. 如何评估时间序列模型的性能？

评估时间序列模型性能的方法包括：

均方误差（MSE）和均方根误差（RMSE）： 衡量预测误差的大小。
平均绝对误差（MAE）： 衡量预测误差的平均值。
AIC 和 BIC： 衡量模型拟合度和复杂性。
图形方法（如残差图）： 检查模型残差的随机性和正态性。

17. 解释一下AIC和BIC？

AIC（赤池信息准则）和BIC（贝叶斯信息准则）是两种常用的模型选择标准，用来评估统计模型的好坏。它们都基于模型的似然函数值，但考虑了模型的复杂度（即参数数量）。

AIC倾向于选择能够更好拟合数据的模型，即使它们更复杂，而BIC则更加偏好简单模型，因为它对复杂度的惩罚更大。通过比较不同模型的AIC或BIC值，我们可以选择最合适的模型，值越小越好。

18. 自相关函数（ACF）如何帮助识别自回归（AR）模型的阶数？

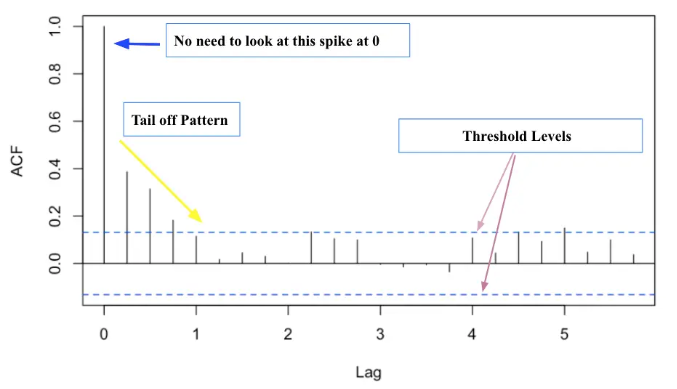
自相关函数（ACF）通过测量时间序列与其滞后值之间的相关性来帮助识别自回归（AR）模型的阶数。在 AR 模型的背景下，ACF 用于分析时间序列值与其过去值在不同滞后期的相关性。ACF 图显示了各种滞后期的相关系数，这些系数的衰减模式有助于确定 AR 模型的适当阶数。具体而言，当 ACF 值急剧下降至接近零的滞后期表明 AR 模型的阶数，因为这标志着过去值不再显著影响当前值。

19. 解释 SARIMA 模型及其适用情况。

季节性自回归积分移动平均(SARIMA) 模型扩展了 ARIMA 模型，通过包含季节成分来解决时间序列数据中的季节性。它通过引入季节性自回归（SAR）、季节性差分（SD）和季节性移动平均（SMA）成分，使其在存在季节模式时效果更佳。

SARIMA 模型适用于具有季节波动的时间序列数据，例如月度销售、季度收入或气候数据，捕捉趋势、季节性和随机波动的相互作用。

20. 为什么不能用简单的回归模型去预测时间序列数据？时间序列模型有哪些不同？

普通的回归模型不适合时间序列数据的预测，因为它们无法处理数据中的时间依赖性、平稳性要求、季节性和周期性变化、自相关性以及动态特性。而时间序列模型专门针对这些问题进行建模和预测。

在处理时间序列数据时，线性回归模型通常会违反以下关键假设：

独立同分布假设（IID假设）：线性回归模型的一个基本假设是观测值之间是独立的，且来自同一分布。这意味着数据点之间不应有系统性的依赖关系。然而，时间序列数据的一个显著特点是数据点之间存在时间上的依赖性。例如，今天的股票价格很可能与昨天的价格高度相关。独立性假设在时间序列数据中显然是不成立的。
误差项的独立性：在线性回归模型中，误差项被假设为相互独立且与自变量无关。但在时间序列数据中，误差项可能具有时间相关性，即一个时间点的误差可能与前一个时间点的误差相关联。例如，季节性影响可能导致特定时间段的误差项表现出规律性的波动。
同方差假设：线性回归模型假设误差项的方差是恒定的，即同方差性。然而，时间序列数据中的误差项方差可能会随着时间变化。例如，经济数据可能在经济繁荣期和衰退期表现出不同的波动性。

时间序列模型专门为处理时间相关的数据而设计，它们通过以下方式解决了上述假设问题：

捕捉时间依赖性：时间序列模型如AR、MA和ARIMA通过引入滞后项和移动平均项，直接建模数据点之间的时间依赖关系。这使得模型能够更准确地反映数据的动态结构。
处理自相关性：时间序列模型通过自回归和移动平均机制，可以有效地处理误差项之间的自相关性。通过分析残差的自相关函数（ACF）和偏自相关函数（PACF），可以诊断并修正模型中的时间依赖性问题。
适应异方差性：对于存在异方差性的时间序列数据，可以使用ARCH/GARCH模型（自回归条件异方差模型/广义自回归条件异方差模型）来建模误差项的方差，解决误差项方差随时间变化的问题。