t-分布随机邻域嵌入 (t-Distributed Stochastic Neighbor Embedding, t-SNE)
t-SNE 是一种非线性降维方法,主要用于高维数据的可视化。它能够将高维数据映射到低维空间,同时保留数据的局部结构。
原理
t-SNE 通过将高维空间中的相似度分布与低维空间中的相似度分布进行匹配,从而实现降维。高维空间中的相似度使用高斯分布建模,低维空间中的相似度使用t分布建模。
公式推理
- 高维空间相似度: 给定高维数据点 xi 和 xj,高维空间中的相似度 pij 定义为:
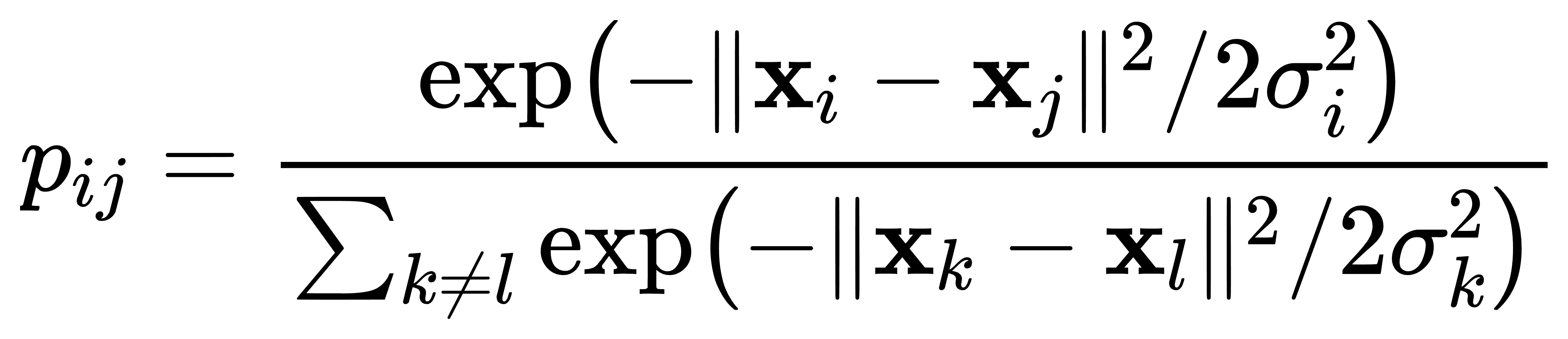
其中,σi 是与数据点 xi 相关的高斯分布的标准差。
- 低维空间相似度: 给定低维数据点 yi 和 yj,低维空间中的相似度 qij 定义为:
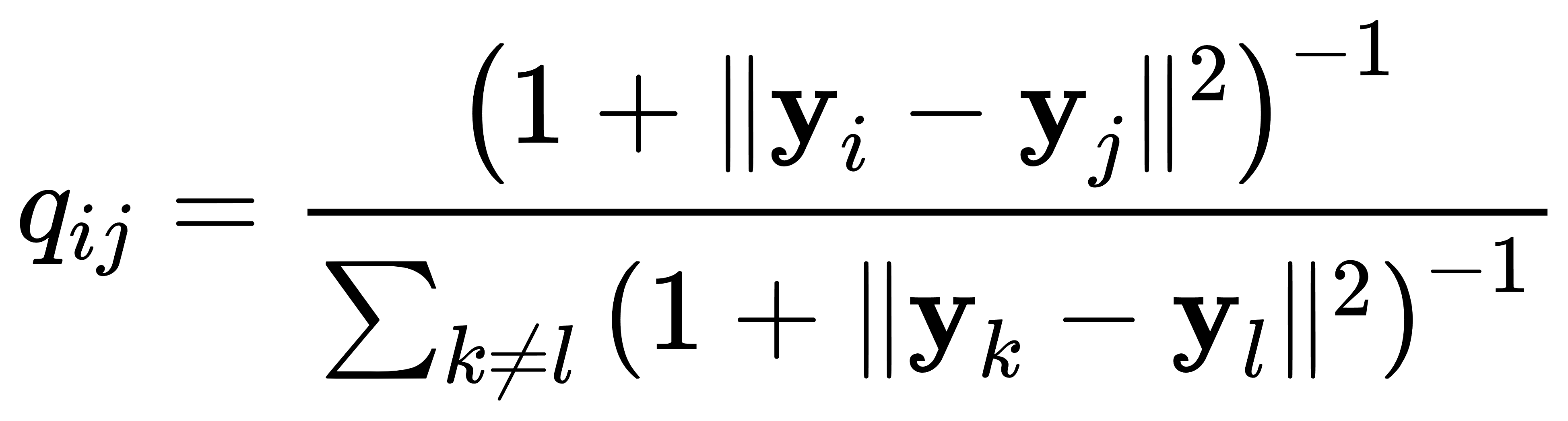
- 优化目标: 最小化高维空间相似度分布和低维空间相似度分布之间的Kullback-Leibler散度:
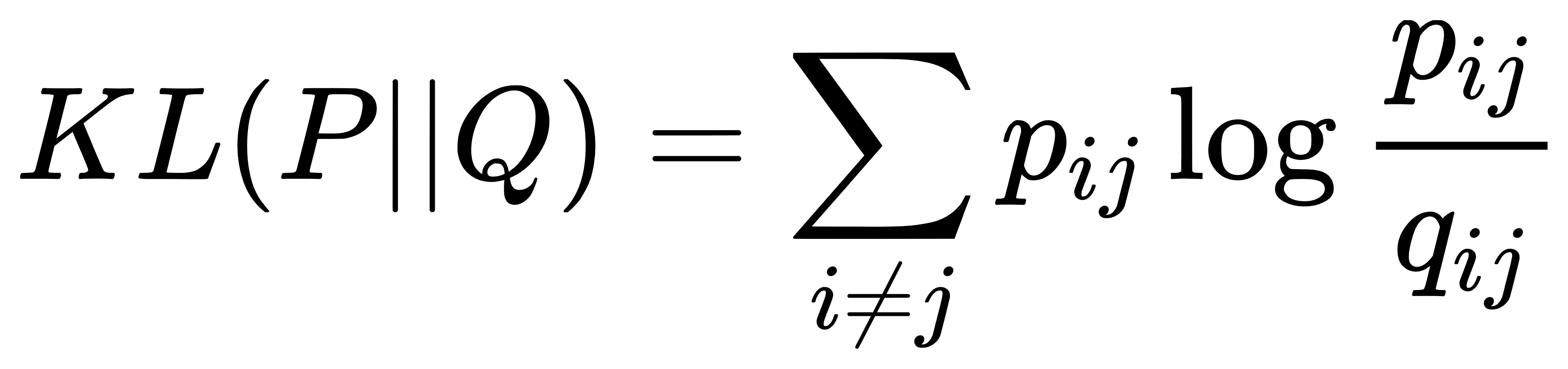
经典案例
案例:t-SNE在手写数字识别数据集上的应用
我们将使用经典的MNIST数据集,它包含了大量的手写数字图片,每张图片是28x28像素的灰度图像,共有10个类别(0到9)。通过t-SNE将MNIST数据集从784维降到2维,并可视化不同数字在降维空间的分布。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler
# 加载MNIST数据集
mnist = fetch_openml('mnist_784', version=1,parser='liac-arff')
X = mnist.data.astype('float64')
y = mnist.target.astype('int64')
# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# 使用t-SNE进行降维到2维
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X_scaled)
# 可视化
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='tab10', edgecolor='k', s=20)
plt.colorbar(scatter, label='Digit', ticks=range(10))
plt.title('t-SNE of MNIST Dataset')
plt.xlabel('Component 1')
plt.ylabel('Component 2')
plt.grid(True)
plt.show()代码解析
- 加载MNIST数据集:使用
fetch_openml函数加载MNIST数据集,包括特征矩阵X和目标向量y。 - 标准化数据:使用
StandardScaler对数据进行标准化处理,使得每个特征具有零均值和单位方差。 - 使用t-SNE进行降维:创建 t-SNE 对象并将数据降到 2 维。
- 可视化:绘制降维后的数据分布,不同颜色表示不同数字类别。
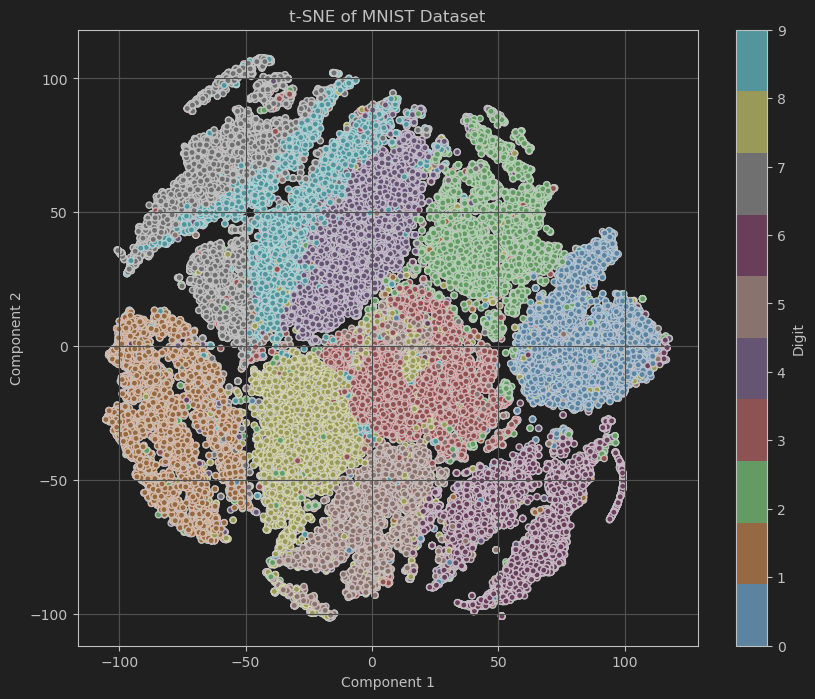
代码展示了如何利用t-SNE对高维数据进行降维,并通过可视化直观地展示了降维后数据的分布情况,有助于理解数据集的结构与特征之间的关系。
多维尺度分析 (Multidimensional Scaling, MDS)
MDS 是一种非线性降维方法,通过保留样本点之间的距离关系将高维数据嵌入低维空间,主要用于数据的可视化和相似性分析。
原理
MDS 试图在低维空间中表示高维空间中的数据点,同时尽可能保留原始数据点之间的距离关系。MDS 的目标是找到一个低维嵌入,使得低维空间中的距离与高维空间中的距离尽可能相似。
公式推理
- 距离矩阵: 给定一个 n×n 的距离矩阵 D,其中 Dij表示数据点 xi 和 xj 之间的距离。
- 嵌入坐标: MDS 寻找一个 n×d 的低维坐标矩阵 Y,使得:

其中,dij(Y) 表示低维空间中数据点 yi 和 yj 之间的欧氏距离。
- 双中心化距离矩阵: 将距离矩阵 D 进行双中心化,得到矩阵 B:
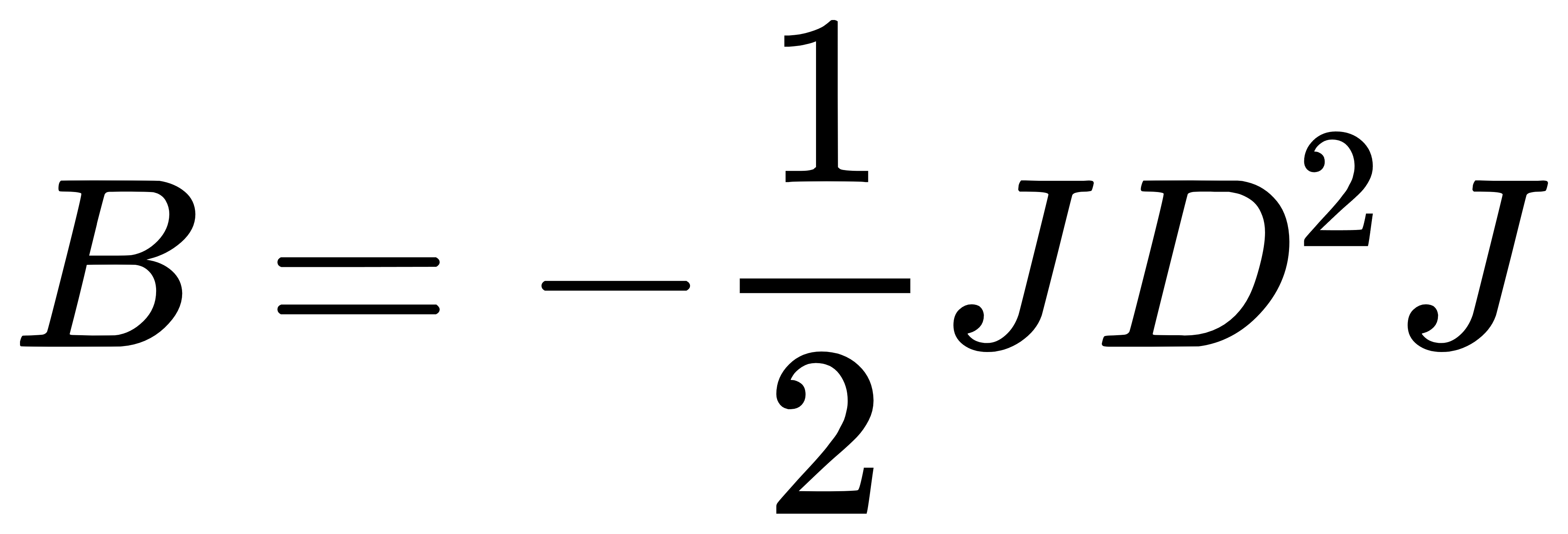
其中,J=I−1/n(11T),I 是单位矩阵,1 是元素全为 1 的向量。
- 特征分解: 对矩阵 B 进行特征值分解,得到特征值和特征向量:
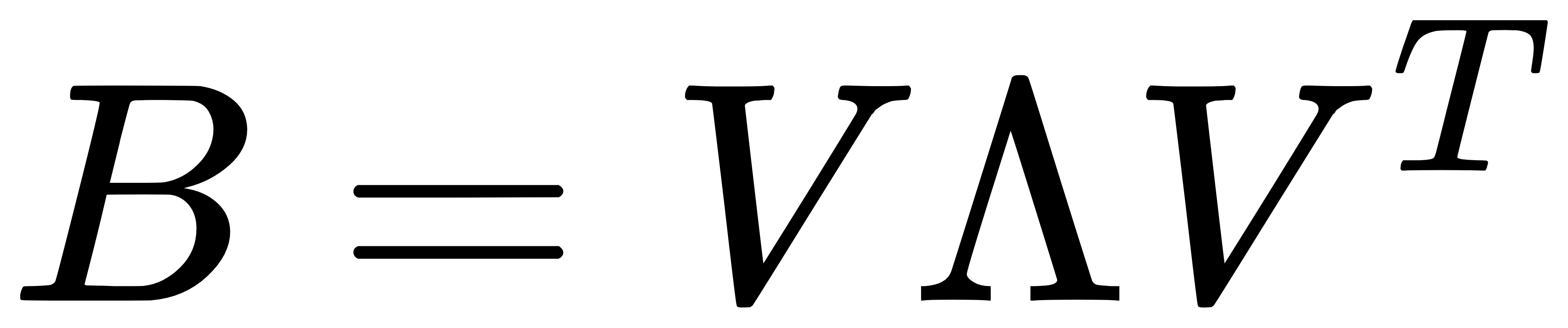
其中,Λ是特征值构成的对角矩阵,V 是特征向量构成的矩阵。
- 低维嵌入: 选择前 d 个最大的特征值及其对应的特征向量,构建低维嵌入:
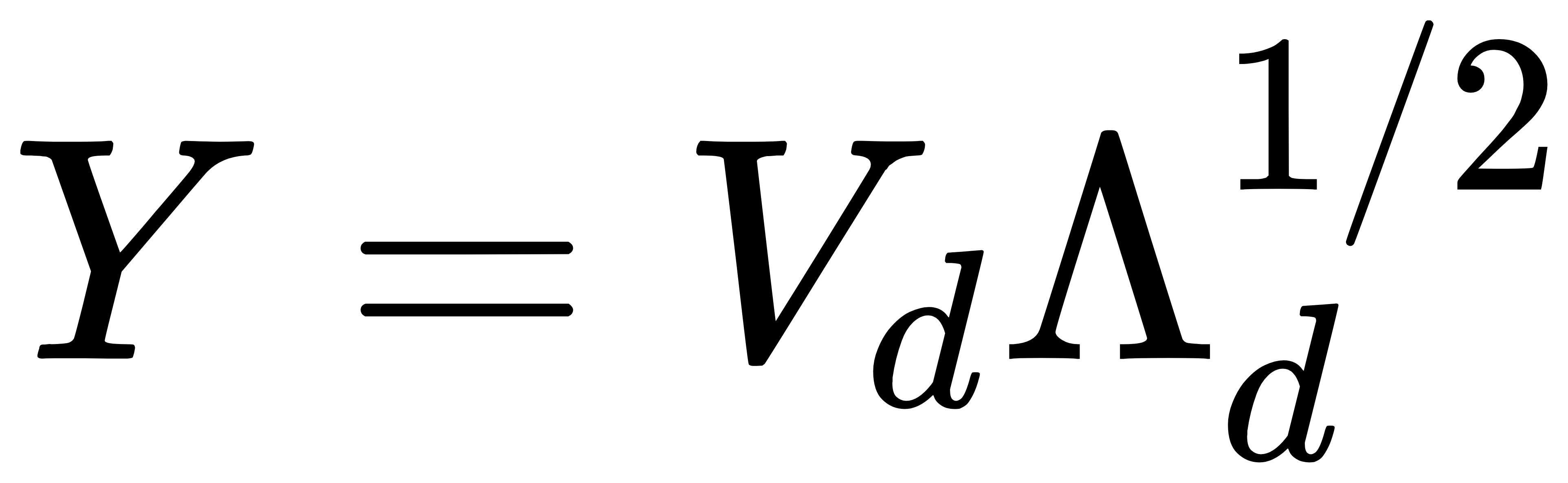
经典案例
案例:MDS在手写数字识别数据集上的应用
我们将使用经典的MNIST数据集,它包含了大量的手写数字图片,每张图片是28x28像素的灰度图像,共有10个类别(0到9)。通过MDS将MNIST数据集从784维降到2维,并可视化不同数字在降维空间的分布。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml
from sklearn.manifold import MDS
from sklearn.preprocessing import StandardScaler
# 加载MNIST数据集
mnist = fetch_openml('mnist_784', version=1)
X = mnist.data.astype('float64').values # 确保转换为numpy数组
y = mnist.target.astype('int64').values
# 减少数据集大小
# 随机选择5000个样本
np.random.seed(42)
indices = np.random.choice(X.shape[0], 5000, replace=False)
X_subset = X[indices]
y_subset = y[indices]
# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X_subset)
# 使用MDS进行降维到2维
mds = MDS(n_components=2, random_state=42)
X_mds = mds.fit_transform(X_scaled) # X_mds 的形状应该是 (5000, 2)
# 可视化
plt.figure(figsize=(10, 8))
scatter = plt.scatter(X_mds[:, 0], X_mds[:, 1], c=y_subset, cmap='tab10', edgecolor='k', s=20)
plt.colorbar(scatter, label='Digit', ticks=range(10))
plt.title('MDS of MNIST Dataset (Subset)')
plt.xlabel('Component 1')
plt.ylabel('Component 2')
plt.grid(True)
plt.show()
代码解析
- 加载MNIST数据集:使用
fetch_openml函数加载MNIST数据集,包括特征矩阵X和目标向量y。 - 标准化数据:使用
StandardScaler对数据进行标准化处理,使得每个特征具有零均值和单位方差。 - 使用MDS进行降维:创建 MDS 对象并将数据降到 2 维。
- 可视化:绘制降维后的数据分布,不同颜色表示不同数字类别。
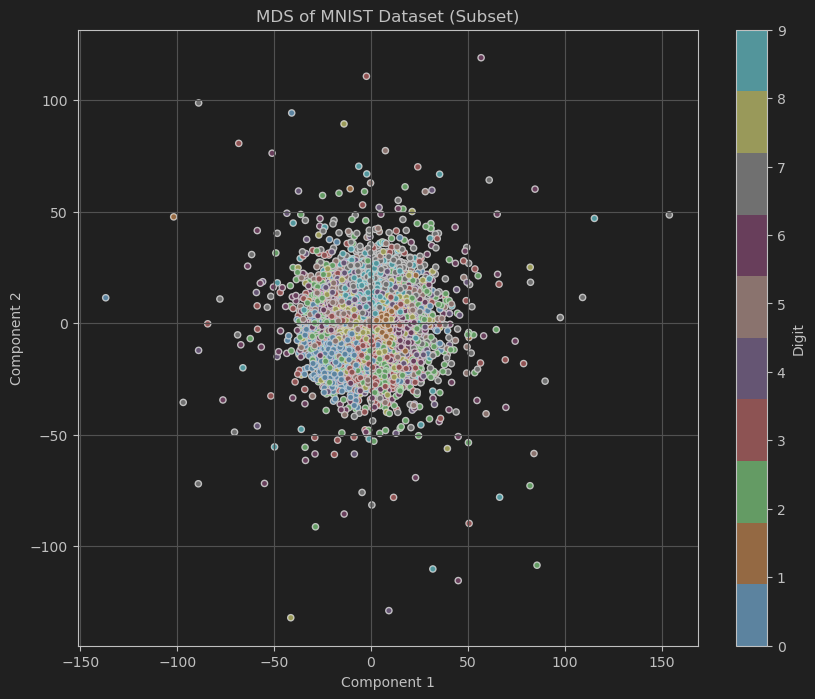
代码展示了如何利用MDS对高维数据进行降维,并通过可视化直观地展示了降维后数据的分布情况,有助于理解数据集的结构与特征之间的关系。