二叉树
什么是二叉树
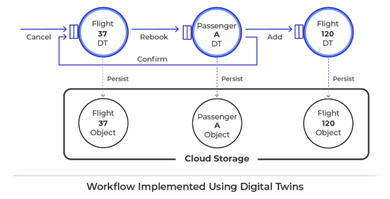
二叉树是一种非线性数据结构(层次关系结构),代表“祖先”与“后代”之间的派生关系,体现了“一分为二”的分治逻辑。与链表类似,二叉树的基本单元是节点,每个节点包含值、左子节点引用和右子节点引用。 首先要明白什么是树,面向对象编程学过吧(c++、Java等),学过Java的更加符合一点,因为取消了多继承,父类和子类的管理图,画出来就是树状的。从一个根节点开始,逐级向下扩展的层次关系。部分家庭还会有家谱,像一个倒着的树(参考成语开枝散叶)。二叉树就是最多一个节点有两个下层节点,而且要知道用哪一个,用左右作为编号。可以理解是链表的分叉形成的。线性—>非线性

- 根节点(root node):位于二叉树顶层的节点,没有父节点。
- 叶节点(leaf node):没有子节点的节点,其两个指针均指向 None 。
边(edge):连接两个节点的线段,即节点引用(指针)。 - 节点所在的层(level):从顶至底递增,根节点所在层为 1 。
- 节点的度(degree):节点的子节点的数量。在二叉树中,度的取值范围是 0、1、2 。
- 二叉树的高度(height):从根节点到最远叶节点所经过的边的数量。
- 节点的深度(depth):从根节点到该节点所经过的边的数量。
- 节点的高度(height):从距离该节点最远的叶节点到该节点所经过的边的数量。
二叉树的实现
TreeNode 类(树节点)
public class TreeNode {
int value;
TreeNode left;
TreeNode right;
public TreeNode(int value) {
this.value = value;
this.left = null;
this.right = null;
}
}
BinaryTree 类(二叉树)
import java.util.LinkedList;
import java.util.Queue;
public class BinaryTree {
private TreeNode root;
public BinaryTree() {
root = null;
}
// 插入一个新的节点
public void insert(int value) {
root = insertRec(root, value);
}
private TreeNode insertRec(TreeNode root, int value) {
if (root == null) {
root = new TreeNode(value);
return root;
}
if (value < root.value) {
root.left = insertRec(root.left, value);
} else if (value > root.value) {
root.right = insertRec(root.right, value);
}
return root;
}
// 删除一个节点
public void delete(int value) {
root = deleteRec(root, value);
}
private TreeNode deleteRec(TreeNode root, int value) {
if (root == null) {
return root;
}
if (value < root.value) {
root.left = deleteRec(root.left, value);
} else if (value > root.value) {
root.right = deleteRec(root.right, value);
} else {
// 节点有一个或没有子节点
if (root.left == null) {
return root.right;
} else if (root.right == null) {
return root.left;
}
// 节点有两个子节点,找到右子树中的最小节点
root.value = minValue(root.right);
// 删除右子树中的最小节点
root.right = deleteRec(root.right, root.value);
}
return root;
}
private int minValue(TreeNode root) {
int minv = root.value;
while (root.left != null) {
minv = root.left.value;
root = root.left;
}
return minv;
}
// 前序遍历
public void preOrderTraversal(TreeNode root) {
if (root != null) {
System.out.print(root.value + " "); // 访问根节点
preOrderTraversal(root.left); // 递归遍历左子树
preOrderTraversal(root.right); // 递归遍历右子树
}
}
// 中序遍历
public void inOrderTraversal(TreeNode root) {
if (root != null) {
inOrderTraversal(root.left); // 递归遍历左子树
System.out.print(root.value + " "); // 访问根节点
inOrderTraversal(root.right); // 递归遍历右子树
}
}
// 后序遍历
public void postOrderTraversal(TreeNode root) {
if (root != null) {
postOrderTraversal(root.left); // 递归遍历左子树
postOrderTraversal(root.right); // 递归遍历右子树
System.out.print(root.value + " "); // 访问根节点
}
}
// 层序遍历
public void levelOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode current = queue.poll();
System.out.print(current.value + " "); // 访问当前节点
if (current.left != null) {
queue.add(current.left); // 将左子节点加入队列
}
if (current.right != null) {
queue.add(current.right); // 将右子节点加入队列
}
}
}
public static void main(String[] args) {
BinaryTree tree = new BinaryTree();
tree.insert(50);
tree.insert(30);
tree.insert(20);
tree.insert(40);
tree.insert(70);
tree.insert(60);
tree.insert(80);
System.out.println("前序遍历:");
tree.preOrderTraversal(tree.root);
System.out.println("\n中序遍历:");
tree.inOrderTraversal(tree.root);
System.out.println("\n后序遍历:");
tree.postOrderTraversal(tree.root);
System.out.println("\n层序遍历:");
tree.levelOrderTraversal(tree.root);
System.out.println("\n删除值 20:");
tree.delete(20);
tree.inOrderTraversal(tree.root);
System.out.println("\n删除值 30:");
tree.delete(30);
tree.inOrderTraversal(tree.root);
System.out.println("\n删除值 50:");
tree.delete(50);
tree.inOrderTraversal(tree.root);
}
}
代码讲解
前序遍历 (Pre-order Traversal)
public void preOrderTraversal(TreeNode root) {
if (root != null) {
System.out.print(root.value + " "); // 访问根节点
preOrderTraversal(root.left); // 递归遍历左子树
preOrderTraversal(root.right); // 递归遍历右子树
}
}
原理:
- 前序遍历的顺序是:根节点 -> 左子树 -> 右子树。
- 首先访问根节点,然后递归地访问左子树,最后递归地访问右子树。这种遍历方式常用于复制树结构,因为先访问根节点可以确保在访问子节点之前先创建根节点。
中序遍历 (In-order Traversal)
public void inOrderTraversal(TreeNode root) {
if (root != null) {
inOrderTraversal(root.left); // 递归遍历左子树
System.out.print(root.value + " "); // 访问根节点
inOrderTraversal(root.right); // 递归遍历右子树
}
}
原理:
- 中序遍历的顺序是:左子树 -> 根节点 -> 右子树。
- 首先递归地访问左子树,然后访问根节点,最后递归地访问右子树。这种遍历方式对于二叉搜索树(BST)会得到一个有序的输出,因为左子树的值都小于根节点,右子树的值都大于根节点。
后序遍历 (Post-order Traversal)
public void postOrderTraversal(TreeNode root) {
if (root != null) {
postOrderTraversal(root.left); // 递归遍历左子树
postOrderTraversal(root.right); // 递归遍历右子树
System.out.print(root.value + " "); // 访问根节点
}
}
原理:
- 后序遍历的顺序是:左子树 -> 右子树 -> 根节点。
- 首先递归地访问左子树,然后递归地访问右子树,最后访问根节点。这种遍历方式常用于删除树结构,因为先删除子节点可以确保在删除根节点之前先删除所有子节点。
层序遍历 (Level-order Traversal)
import java.util.LinkedList;
import java.util.Queue;
public void levelOrderTraversal(TreeNode root) {
if (root == null) {
return;
}
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
TreeNode current = queue.poll();
System.out.print(current.value + " "); // 访问当前节点
if (current.left != null) {
queue.add(current.left); // 将左子节点加入队列
}
if (current.right != null) {
queue.add(current.right); // 将右子节点加入队列
}
}
}
原理:
- 层序遍历的顺序是:从上到下,从左到右逐层访问每个节点。
- 使用队列来实现层序遍历。首先将根节点入队,然后循环从队列中取出节点并访问,同时将其左右子节点入队。这种遍历方式可以逐层访问树的节点,常用于树的宽度优先搜索(BFS)。
二叉树的类型
二叉树根据其特性还可以分为多种类型,如:
完全二叉树:除了最后一层,其他层的所有节点都有两个子节点,最后一层的节点从左到右连续排列。

满二叉树:每个节点都有两个子节点,树的所有层都被填满。

平衡二叉树:所有节点的左右子树的高度差不超过1。

怎么用二叉树
在网页开发中,二叉树及其变种结构在多个方面都能找到应用,包括但不限于DOM树操作、数据组织、动画和游戏开发等。以下是一些具体的应用场景和代码示例,展示如何在网页开发中利用二叉树结构解决实际问题。
1. DOM树操作
应用场景:操作DOM树来动态更新网页内容。
说明:DOM(Document Object Model)树是HTML和XML文档的树状表示。JavaScript可以操作DOM树来动态地更新网页内容。每个节点表示文档的一部分(如元素、属性、文本等),可以使用递归遍历技术来高效地操作这些节点。
<!DOCTYPE html>
<html>
<head>
<title>DOM Tree Traversal</title>
</head>
<body>
<div id="root">
<p>Paragraph 1</p>
<div>
<p>Paragraph 2</p>
<span>Span 1</span>
</div>
<p>Paragraph 3</p>
</div>
<script>
document.addEventListener("DOMContentLoaded", function() {
const rootElement = document.getElementById("root");
traverseDOM(rootElement);
});
function traverseDOM(node) {
if (node) {
console.log(node.nodeName); // 访问节点
for (let child of node.childNodes) {
traverseDOM(child); // 递归遍历子节点
}
}
}
</script>
</body>
</html>
2. 树形菜单
应用场景:创建动态的树形菜单或目录结构。
说明:树形菜单是一种常见的UI组件,广泛用于文件管理系统、网站导航等场景。树结构的节点动态展开和折叠,可以使用递归来构建和操作这些节点。
<!DOCTYPE html>
<html>
<head>
<title>Tree Menu</title>
<style>
ul, #myUL {
list-style-type: none;
}
#myUL {
margin: 0;
padding: 0;
}
.caret {
cursor: pointer;
user-select: none; /* 禁止文本选择 */
}
.caret::before {
content: "\25B6";
color: black;
display: inline-block;
margin-right: 6px;
}
.caret-down::before {
transform: rotate(90deg);
}
.nested {
display: none;
}
.active {
display: block;
}
</style>
</head>
<body>
<h2>Tree Menu</h2>
<ul id="myUL">
<li><span class="caret">Parent 1</span>
<ul class="nested">
<li>Child 1</li>
<li>Child 2</li>
</ul>
</li>
<li><span class="caret">Parent 2</span>
<ul class="nested">
<li>Child 3</li>
<li>Child 4</li>
</ul>
</li>
</ul>
<script>
document.addEventListener("DOMContentLoaded", function() {
var toggler = document.getElementsByClassName("caret");
for (let i = 0; i < toggler.length; i++) {
toggler[i].addEventListener("click", function() {
this.parentElement.querySelector(".nested").classList.toggle("active");
this.classList.toggle("caret-down");
});
}
});
</script>
</body>
</html>
3. 客户端路由
应用场景:实现单页应用(SPA)的客户端路由。
说明:单页应用中的客户端路由可以利用树形结构来管理和匹配不同的路由路径。每个节点表示一个路由,路径的层次结构可以通过树结构表示。
class RouteNode {
constructor(path, component) {
this.path = path;
this.component = component;
this.children = [];
}
addChild(child) {
this.children.push(child);
}
match(path) {
if (path === this.path) {
return this.component;
}
for (let child of this.children) {
const result = child.match(path);
if (result) {
return result;
}
}
return null;
}
}
class Router {
constructor() {
this.root = new RouteNode('/', 'RootComponent');
}
addRoute(path, component) {
const segments = path.split('/').filter(s => s.length > 0);
let currentNode = this.root;
for (let segment of segments) {
let found = false;
for (let child of currentNode.children) {
if (child.path === segment) {
currentNode = child;
found = true;
break;
}
}
if (!found) {
const newNode = new RouteNode(segment, null);
currentNode.addChild(newNode);
currentNode = newNode;
}
}
currentNode.component = component;
}
navigate(path) {
const component = this.root.match(path);
if (component) {
console.log(`Navigating to ${path}, load component: ${component}`);
} else {
console.log(`No route matched for path: ${path}`);
}
}
}
// 示例用法
const router = new Router();
router.addRoute('/home', 'HomeComponent');
router.addRoute('/about', 'AboutComponent');
router.addRoute('/about/team', 'TeamComponent');
router.navigate('/home'); // 输出:Navigating to /home, load component: HomeComponent
router.navigate('/about/team'); // 输出:Navigating to /about/team, load component: TeamComponent
4. 数据可视化
应用场景:使用树图展示层次结构数据。
说明:树图是一种用于展示层次结构数据的可视化图表。在网页中,可以使用树图来展示组织结构、文件目录等数据,常用的库如D3.js可以方便地创建树图。
<!DOCTYPE html>
<html>
<head>
<title>Tree Diagram</title>
<script src="https://d3js.org/d3.v6.min.js"></script>
<style>
.node circle {
fill: #999;
}
.node text {
font: 12px sans-serif;
}
.link {
fill: none;
stroke: #555;
stroke-width: 1.5px;
}
</style>
</head>
<body>
<h2>Tree Diagram</h2>
<svg width="600" height="400"></svg>
<script>
const data = {
name: "Root",
children: [
{
name: "Child 1",
children: [
{ name: "Grandchild 1" },
{ name: "Grandchild 2" }
]
},
{ name: "Child 2" }
]
};
const width = 600;
const height = 400;
const svg = d3.select("svg"),
margin = { top: 20, right: 120, bottom: 20, left: 120 },
g = svg.append("g").attr("transform", "translate(" + margin.left + "," + margin.top + ")");
const tree = d3.tree().size([height - margin.top - margin.bottom, width - margin.left - margin.right]);
const root = d3.hierarchy(data);
tree(root);
const link = g.selectAll(".link")
.data(root.descendants().slice(1))
.enter().append("path")
.attr("class", "link")
.attr("d", d => {
return "M" + d.y + "," + d.x
+ "C" + (d.y + d.parent.y) / 2 + "," + d.x
+ " " + (d.y + d.parent.y) / 2 + "," + d.parent.x
+ " " + d.parent.y + "," + d.parent.x;
});
const node = g.selectAll(".node")
.data(root.descendants())
.enter().append("g")
.attr("class", d => "node" + (d.children ? " node--internal" : " node--leaf"))
.attr("transform", d => "translate(" + d.y + "," + d.x + ")");
node.append("circle")
.attr("r", 10);
node.append("text")
.attr("dy", 3)
.attr("x", d => d.children ? -12 : 12)
.style("text-anchor", d => d.children ? "end" : "start")
.text(d => d.data.name);
</script>
</body>
</html>
5. 游戏开发中的场景管理
应用场景:在网页游戏中管理和渲染场景。
说明:在网页游戏开发中,可以使用场景图来组织和管理游戏场景中的对象。每个节点表示一个游戏对象(如角色、道具、背景等),场景图有助于实现对象的层次管理和渲染顺序。
<!DOCTYPE html>
<html>
<head>
<title>Game Scene Graph</title>
<style>
canvas {
border: 1px solid black;
}
</style>
</head>
<body>
<canvas id="gameCanvas" width="600" height="400"></canvas>
<script>
class SceneNode {
constructor(name) {
this.name = name;
this.children = [];
}
addChild(child) {
this.children.push(child);
}
render(ctx) {
ctx.fillText(this.name, Math.random() * 600, Math.random() * 400); // 随机位置渲染
for (let child of this.children) {
child.render(ctx);
}
}
}
document.addEventListener("DOMContentLoaded", function() {
const canvas = document.getElementById("gameCanvas");
const ctx = canvas.getContext("2d");
ctx.font = "20px Arial";
const root = new SceneNode("Root");
const child1 = new SceneNode("Child1");
const child2 = new SceneNode("Child2");
root.addChild(child1);
root.addChild(child2);
root.render(ctx); // 渲染场景图
});
</script>
</body>
</html>
二叉树及其变种在网页开发中有广泛的应用,包括但不限于DOM树操作、树形菜单、客户端路由、数据可视化和游戏场景管理。这些应用场景展示了二叉树结构如何在实际开发中解决各种问题,提高代码的组织和操作效率。通过掌握这些技术,可以更高效地开发和维护复杂的网页应用。
持续更新中~~ 欢迎评论留言
- 从0开始的算法(数据结构和算法)基础(一)
- 从0开始的算法(数据结构和算法)基础(二)
- 从0开始的算法(数据结构和算法)基础(三)
- 从0开始的算法(数据结构和算法)基础(四)
- 从0开始的算法(数据结构和算法)基础(五)