PDF文档公众号回复关键字:20240805

1 完善程序 (单选题 ,每小题3分,共30分)
计数排序
计数排序是一个广泛使用的排序方法。下面的程序使用双关键字计数排序,将 n 对 10000以内的整数,从小到大排序。
例如有三对整数 (3,4)、(2,4)、(3,3),那么排序之后应该是 (2,4)、(3,3)、(3,4) 。
输入第一行为 n,接下来 n 行,第 i 行有两个数 a[i] 和 b[i],分别表示第 i 对整数的第一关键字和第二关键字。
从小到大排序后输出。
数据范围 1<n<10^7,1<a[i],b[i]< 10^4。
提示:应先对第二关键字排序,再对第一关键字排序。数组 ord[] 存储第二关键字排序的结果,数组 res[] 存储双关键字排序的结果。
试补全程序。
01 #include <cstdio>
02 #include <cstring>
03 using namespace std;
04 const int maxn = 10000000;
05 const int maxs = 10000;
06
07 int n;
08 unsigned a[maxn], b[maxn],res[maxn], ord[maxn];
09 unsigned cnt[maxs + 1];
10 int main() {
11 scanf("%d", &n);
12 for (int i = 0; i < n; ++i)
13 scanf("%d%d", &a[i], &b[i]);
14 memset(cnt, 0, sizeof(cnt));
15 for (int i = 0; i < n; ++i)
16 ①; // 利用 cnt 数组统计数量
17 for (int i = 0; i < maxs; ++i)
18 cnt[i + 1] += cnt[i];
19 for (int i = 0; i < n; ++i)
20 ②; // 记录初步排序结果
21 memset(cnt, 0, sizeof(cnt));
22 for (int i = 0; i < n; ++i)
23 ③; // 利用 cnt 数组统计数量
24 for (int i = 0; i < maxs; ++i)
25 cnt[i + 1] += cnt[i];
26 for (int i = n - 1; i >= 0; --i)
27 ④ // 记录最终排序结果
28 for (int i = 0; i < n; i++)
29 printf("%d %d", ⑤);
30
31 return 0;
32}
1 ①处应填( )[3分]
A ++cnt [i]
B ++cnt[b[i]]
C ++cnt[a[i] * maxs + b[i]]
D ++cnt[a[i]]
2 ②处应填( )[3分]
A ord[–cnt[a[i]]] = i
B ord[–cnt[b[i]]] = a[i]
C ord[–cnt[a[i]]] = b[i]
D ord[–cnt[b[i]]] = i
3 ③处应填( )[3分]
A ++cnt[b[i]]
B ++cnt[a[i] * maxs + b[i]]
C ++cnt[a[i]]
D ++cnt [i]
4.④处应填( )[3分]
A res[–cnt[a[ord[i]]]] = ord[i]
B res[–cnt[b[ord[i]]]] = ord[i]
C res[–cnt[b[i]]] = ord[i]
D res[–cnt[a[i]]] = ord[i]
5 ⑤处应填( )[3分]
A a[i], b[i]
B a[res[i]], b[res[i]]
C a[ord[res[i]]]j b[ord[res[i]]]
D a[res[ord[i]]]j b[res[ord[i]]]
2 相关知识点
1) 计数排序
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用,具体思路为
统计相同元素出现次数
根据统计的结果将序列回收到原来的序列中
#include<bits/stdc++.h>
using namespace std;
int main(){
int a[10]={3,4,2,7,5,4,3,3,3,5};
int cnt[7]={0};//cnt数组记录对应下标出现次数
for(int i=0;i<10;i++){
cnt[a[i]]++;
}
for(int i=0;i<=7;i++){//枚举对应范围的数 从最小到最大,本示例从0~7即可
while(cnt[i]>0){//一个数字出现多次时,cnt[i]为对应的数为出现几次
cout<<i<<" ";
cnt[i]--;
}
}
return 0;
}
/*
输出
2 3 3 3 3 4 4 5 5 7
*/
2) 前缀和
前缀和就是数组的前i项之和
s[1]=a[1]
s[2]=a[1]+a[2]
s[3]=a[1]+a[2]+a[3]
s[4]=a[1]+a[2]+a[3]+a[4]
s[5]=a[1]+a[2]+a[3]+a[4]+a[5]
#include<bits/stdc++.h>
using namespace std;
int main(){
int a[10]={1,2,3,4,5,6,7,8,9,10};
int s[10]={0};//存放前i项和数组
int sum=0;//累加变量
for(int i=0;i<10;i++){
sum+=a[i];
s[i]+=sum;
}
for(int i=0;i<10;i++){
cout<<s[i]<<" ";
}
return 0;
}
/*
输出
1 3 6 10 15 21 28 36 45 55
*/
3) 计数排序与前缀和
计数排序和前缀和结合,把通过一个排序数组记录待排序数组的下标
#include<bits/stdc++.h>
using namespace std;
/*
计数排序和前缀和结合,可以和原数组的数一一对应
*/
int main(){
int a[10]={3,4,2,7,5,4,3,3,3,5};
int b[10]={0};//从小到大记录对应数在a数组的下标
int cnt[15]={0};//cnt数组记录对应下标出现次数
for(int i=0;i<10;i++){//累加a数组每个数出现次数
cnt[a[i]]++;
}//0 0 1 4 2 2 0 1 0 0
for(int i=0;i<15;i++){//前缀和计算 为a中每个数计算一个对应下标
cnt[i+1]+=cnt[i];
}//0 0 1 5 7 9 9 10 10 10
for(int i=0;i<10;i++){//把a数组数放入b数组通过下标排序,值为a数组的下标
b[--cnt[a[i]]]=i;
}//2 3 3 3 3 4 4 5 5 7
return 0;
}
/*
输出
2 3 3 3 3 4 4 5 5 7
*/
4) 后缀自增和前缀自增
前缀自增 ++i,后缀自增i++
i++只有i变量加+1,i++的表达式不加+1
++i则变量加1,++i表达式加1
#include<bits/stdc++.h>
using namespace std;
int main(){
int a[5]={0,1,2,3,4};
int i=0;
cout<<a[i++]<<endl;//i++表达式不加,输出a[0]的值,对应为0
i=0;
cout<<a[++i]<<endl;//++i表达式加1,输出a[1]的值,对应为1
i=0;
i++;
cout<<a[i]<<endl;//i++后i变量加1, 出a[1]的值,对应为1
i=0;
++i;
cout<<a[i]<<endl;//++i后i变量加1, 出a[1]的值,对应为1
return 0;
}
3 思路分析
1 ①处应填( B )[3分]
A ++cnt [i]
B ++cnt[b[i]]
C ++cnt[a[i] * maxs + b[i]]
D ++cnt[a[i]]
分析
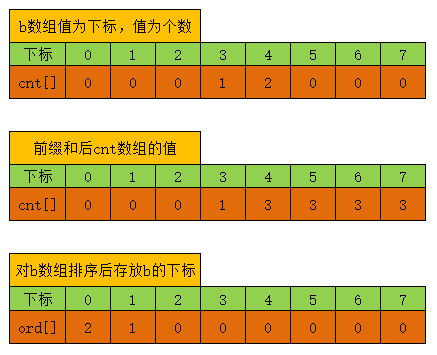
通过cnt数组对b数组进行排序,如果有重复会累加到cnt当前元素中
例如
int b[3]={4,4,3}
cnt数组的值如下图

2 ②处应填( D )[3分]
A ord[–cnt[a[i]]] = i
B ord[–cnt[b[i]]] = a[i]
C ord[–cnt[a[i]]] = b[i]
D ord[–cnt[b[i]]] = i
分析
在ord数组中,从小到大记录b数组的位置
ord[0]=2 对应b[2]=3
ord[1]=1 对应b[1]=4
ord[2]=0 对应b[0]=4
3 ③处应填( C )[3分]
A ++cnt[b[i]]
B ++cnt[a[i] * maxs + b[i]]
C ++cnt[a[i]]
D ++cnt [i]
分析
进行这里之前,对cnt数组进行了清0
21 memset(cnt, 0, sizeof(cnt));
通过cnt数组对a数组进行排序,如果有重复会累加到cnt当前元素中
例如
int a[3]={3,2,3}
cnt数组的值如下图
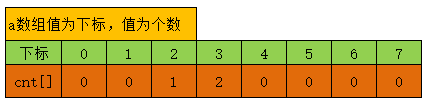
4.④处应填( A )[3分]
A res[–cnt[a[ord[i]]]] = ord[i]
B res[–cnt[b[ord[i]]]] = ord[i]
C res[–cnt[b[i]]] = ord[i]
D res[–cnt[a[i]]] = ord[i]
分析
在res数组中,从小到大记录b数组的下标,b数组下标和a数组下标对应
a[ord[i]] ord[]已经对b进行了排序,n-1~0 从大到小找对应的a
cnt[a[ord[i]]] 找到a后,以下标放入res数组,进行计数排序
res[--cnt[a[ord[i]]]] = ord[i] --用ord[i]赋值,记录res[]存放的b数组下标
例如
int a[3]={3,2,3}
int b[3]={4,4,3}
res[--cnt[a[ord[2]]]]= res[--cnt[a[0]]]=res[--cnt[3]]=res[2]
=ord[2]=0
res[--cnt[a[ord[1]]]]= res[--cnt[a[1]]]=res[--cnt[2]]=res[0]
=ord[1]=1
res[--cnt[a[ord[0]]]]= res[--cnt[a[2]]]=res[--cnt[3]]=res[1]
=ord[0]=2

26 for (int i = n - 1; i >= 0; --i)
因为ord[]是从小到大,从n-1~0,从大到小循环,a相同时,取出的第1次取出的下标大,可以对应
如果从0~n-1循环,正好相反,导致b排序不对
5 ⑤处应填( B )[3分]
A a[i], b[i]
B a[res[i]], b[res[i]]
C a[ord[res[i]]]j b[ord[res[i]]]
D a[res[ord[i]]]j b[res[ord[i]]]
分析
res[]对a和b数组进行计数排序,按a数组从小到大,如果a相同按b数组从小到大
res[]数组的值分别位a和b数组的下标,a和b数组下标对应
所以按res下标从小到大输出a和b的值即可