目录
1、什么是超前进位加法器
2、CLA加法器的关键路径
3、CLA加法器的Verilog实现
4、CLA加法器的时序性能
5、总结
文章总目录点这里:《基于FPGA的数字信号处理》专栏的导航与说明
1、什么是超前进位加法器
在之前的文章,我们介绍了行波进位加法器(RCA)。RCA有一个很大的缺点就是关键路径延迟非常高,而之所以高完全是因为进位路径太长了,如果我们能想办法缩短进位路径,那就可以提高加法器的速度。
RCA的缺点在于第k位的进位Ck必须依赖于前一级的Ck-1,最高位的进位将必须等待之前所有级进位计算完毕后才能计算出结果。所以,超前进位加法器的核心思想是并行计算进位Ck。
对于任何一个全加器都有:
s = a ^ b ^ cin
cout = ab + cin(a ^ b)
观察上式s和c,将共有部分分别定义为:

其中的G是generate,它表示只有当ab均为1时才为1,说明此时 生成 了进位;P是propagate,它表示只有当ab不同时才为1,说明此时的进位才能 传播 到高位。例如ab不同,如 xxx1 + xxx0,此时的低位进位若为1,这个进位就可以被传递到高位,因为 1 + 0 + 1 一定会产生进位。若ab相同,如 xxx1 + xxx1 ,此时不管低位进位是0还是1,都会被卡在最低位,因为1 + 1 一定等与0,此时的进位是由这一位的加法产生的,而和来自低位的进位无关。
仍以2个4bits数的加法为例,将上式代入的到他们的逻辑表达式,有:
c1 = g0 + c0 · p0
c2 = g1 + c1 · p1
c3 = g2 + c2 · p2
c4 = g3 + c3 · p3
上面的式子可以被展开,如下:
c1 = g0 + c0 · p0
c2 = g1 + c1 · p1 = g1 + p1 · (g0 + c0 · p0) = g1 + p1 · g0 + c0 · p0 · p1
c3 = g2 + c2 · p2 = g2 + p2 · (g1 + p1 · (g0 + c0 · p0) ) = g2 + p2 · g1 + p2 · p1 · g0 + p2 · p1 · p0 · c0
c4 = g3 + c3 · p3 = g3 + p3 · (g2 + p2 · (g1 + p1 · (g0 + c0 · p0) )) = g3 + p3 · g2 +p3 · p2 · g1 + p3 · p2 · p1 · g0 + p3 · p2 · p1 · p0 · c0
和的部分可以写成如下形式:
s0 = p0 ^ c0
s1 = p1 ^ c1
s2 = p2 ^ c2
s3 = p3 ^ c3
根据上述式子,可以推断出电路的结构示意图,这种加法器就叫做超前进位加法器(Carry Lookahead Adder,CLA):
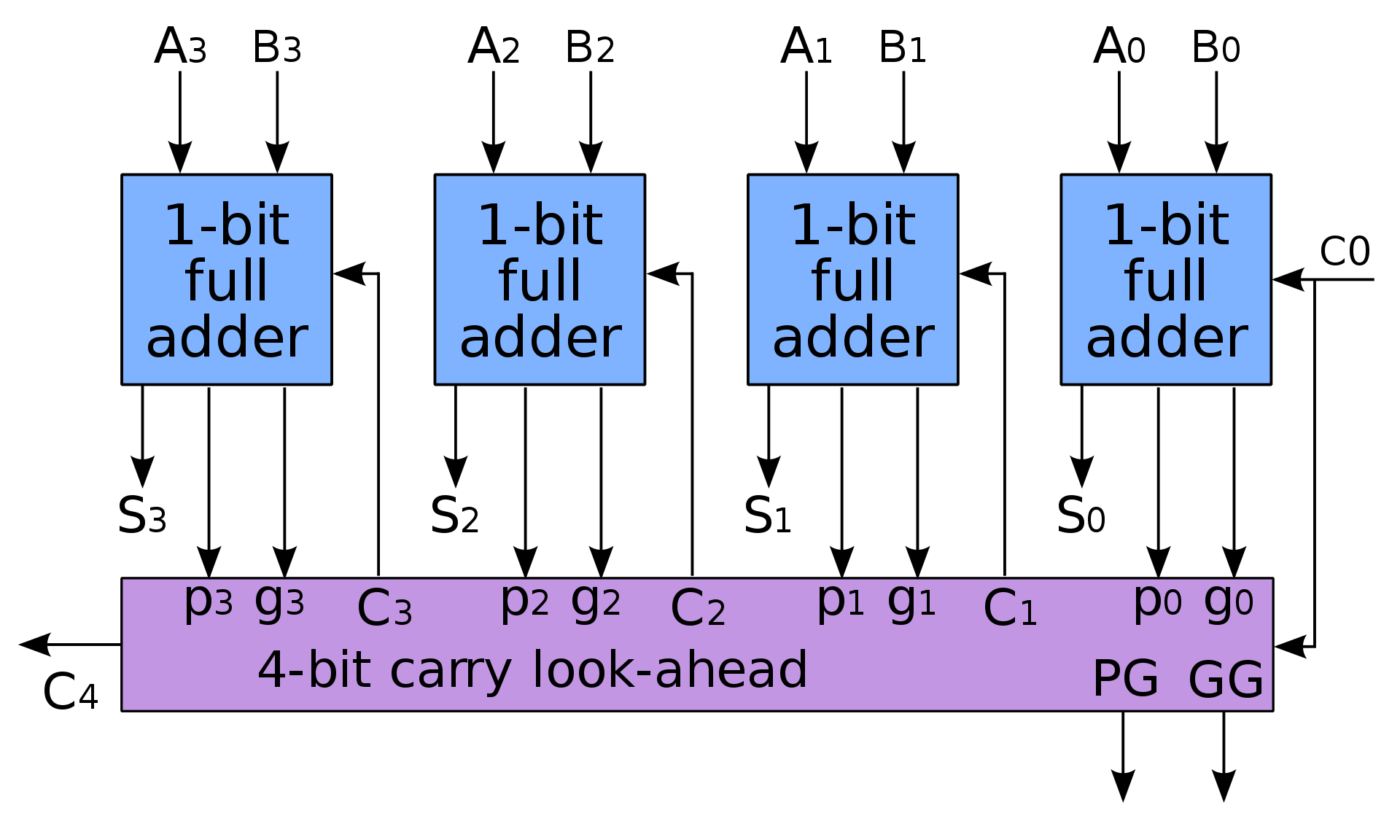
2、CLA加法器的关键路径
从上面的公式推断似乎只发现了CLA的电路面积巨大,而没有看出来速度快啊?接下来分析一下CLA电路关键路径的延迟。首先是进位链的延迟:
c1 = g0 + c0 · p0,g0和p0都需要一个门电路,c0 · p0需要一个门电路,g0 + c0 · p0需要一个门电路,所以最终的延迟为3个门电路
c2 = g1 + p1 · g0 + c0 · p0 · p1,同理需要3个门电路
c3和c4同样需要3个门电路
其中,c4的电路结构如下:
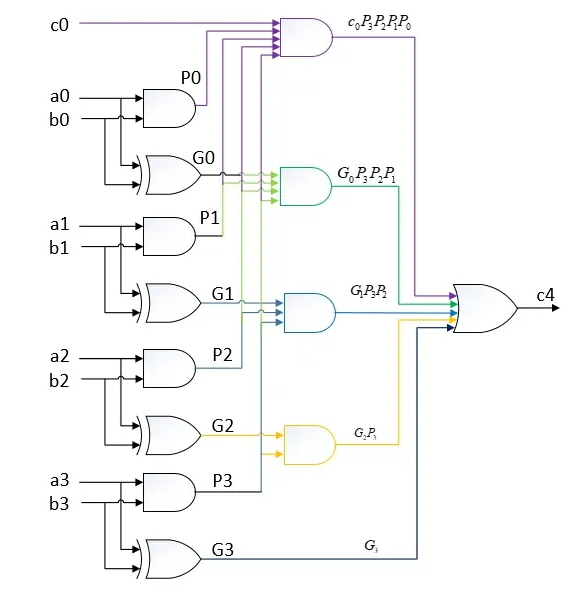
以上说明进位链延迟都是3个门电路,同时别忘了,和的输出是要用到进位的:
s0 = p0 ^ c0
s1 = p1 ^ c1
s2 = p2 ^ c2
s3 = p3 ^ c3
所以,整个电路的关键路径已经不是进位了,而是和,此时的延迟是 3 + 1 = 4个门电路延迟!
为什么CLA电路的进位的延迟小了这么多呢?很简单,面积换时间!从上面也可以看到,由于进位都是同时并行计算出来的,所以用到的电路面积特别大,单单计算一个c4就用了13个门电路(其中一些门电路还是3输入/4输入的)。可以预见,随着加法器位宽的增加,电路面积也会爆炸式地增加!
对于较大位宽的加法器,可以设计成多个CLA级联的形式,例如16bits数的加法,可以设计成4个CLA电路级联,这样的电路既有 “超前进位” 的部分,也有 “行波进位” 的部分 。如下:
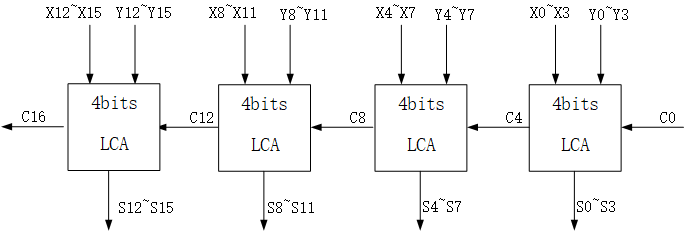
总而言之,RCA的缺点在于关键路径长,限制了速度;CLA关键路径短,速度快,进位链计算依赖少,但对于位宽较大的加法器,PG和进位生成逻辑大,存在较大扇入扇出,变化信号多,会有较多的glitch,且面积与复杂度比同等的RCA大。
3、CLA加法器的Verilog实现
根据上面的公式和结构示意图,可以很容易地写出两个4bits数的CLA加法器的verilog代码:
//cla加法器
module cla(
input [3:0] x, //加数1
input [3:0] y, //加数2
input cin, //来自低位的进位
output [3:0] sum, //和
output cout //向高位的进位
);
wire [4:0] c; //进位连接变量
wire [3:0] g; //generate变量
wire [3:0] p; //propagate变量
assign cout = c[4];
//生成和
assign sum = p ^ c[3:0];
//生成进位
assign c[0] = cin;
assign c[4:1] = g | (c & p);
assign p = x ^ y; //生成propagate信号
assign g = x & y; //生成generate信号
endmodule 生成的示意图如下(这个排布不能很好地看出来层次结构,但确实没错):
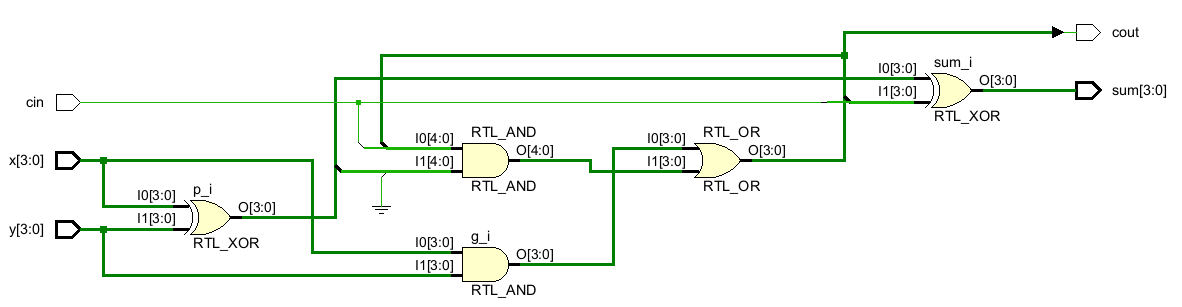
然后写个TB测试一下这个加法器电路,因为4个bits即16×16=256种情况,加上低位借位的两种情况,也才256×2=512种情况,所以可以用穷举法来测试:
`timescale 1ns/1ns //时间刻度:单位1ns,精度1ns
module tb_cla();
//定义变量
reg [3:0] x; //加数1
reg [3:0] y; //加数2
reg cin; //来自低位的进位
wire [3:0] sum; //和
wire cout; //向高位进位
reg [3:0] sum_real; //和的真实值,作为对比
reg cout_real; //向高位进位的真实值,作为对比
wire sum_flag; //sum正确标志信号
wire cout_flag; //cout正确标志信号
assign sum_flag = sum == sum_real; //和的结果正确时拉高该信号
assign cout_flag = cout == cout_real; //进位结果正确时拉高该信号
integer z,i,j; //循环变量
//设置初始化条件
initial begin
//初始化
x =1'b0;
y =1'b0;
cin =1'b0;
//穷举所有情况
for(z=0;z<=1;z=z+1)begin
cin = z;
for(i=0;i<16;i=i+1)begin
x = i;
for(j=0;j<16;j=j+1)begin
y = j;
if((i+j+z)>15)begin //如果加法的结果产生了进位
sum_real = (i+j+z) - 16; //减掉进位值
cout_real = 1; //向高位的进位为1
end
else begin //如果加法的结果没有产生了进位
sum_real = i+j+z; //结果就是加法本身
cout_real = 0; //向高位的进位为0
end
#5;
end
end
end
#10 $stop(); //结束仿真
end
//例化被测试模块
cla u_cla(
.x (x),
.y (y),
.sum (sum),
.cin (cin),
.cout (cout)
);
endmoduleTB中分别用3个嵌套循环将所有情况穷举出来,即cin=0~1、x=0~15和y=0~15的所有情况。加法运算的预期结果也是很容易就可以找出来的,就是在TB中直接写加法就行。接着构建了两个标志向量sum_flag和cout_flag作为电路输出与预期结果的对比值,当二者一致时即拉高这两个信号。这样我们只要观察这两个信号,即可知道电路输出是否正确。仿真结果如下:
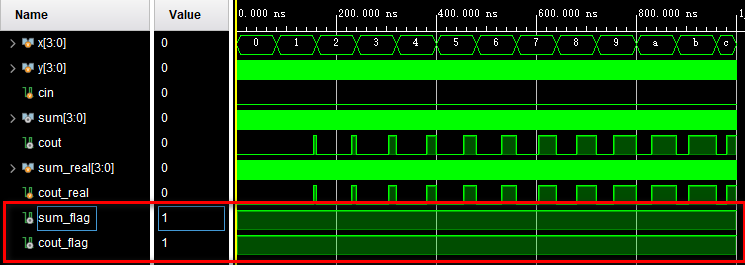
可以看到,sum_flag和cout_flag都是一直拉高的,说明电路输出正确。
为了满足不同位宽的加法,这里也给出参数化设计形式的Verilog代码:
//cla加法器
module cla
#(
parameter integer WIDTH = 4
)
(
input [WIDTH-1:0] x, //加数1
input [WIDTH-1:0] y, //加数2
input cin, //来自低位的进位
output [WIDTH-1:0] sum, //和
output cout //向高位的进位
);
wire [WIDTH :0] c; //进位连接变量
wire [WIDTH-1:0] g; //generate变量
wire [WIDTH-1:0] p; //propagate变量
assign cout = c[WIDTH];
//生成和
assign sum = p ^ c[WIDTH-1:0];
//生成进位
assign c[0] = cin;
assign c[WIDTH:1] = g | (c & p);
assign p = x ^ y; //生成propagate信号
assign g = x & y; //生成generate信号
endmodule4、CLA加法器的时序性能
为了探究CLA加法器的时序性能,需要再原有代码的基础上,做一些小小的改变:在输入和输出分别添加上寄存器。如下:
//cla加法器
module cla
#(
parameter integer WIDTH = 8
)
(
input clk,
input [WIDTH-1:0] x, //加数1
input [WIDTH-1:0] y, //加数2
input cin, //来自低位的进位
output [WIDTH-1:0] sum, //和
output cout //向高位的进位
);
wire [WIDTH :0] c; //进位连接变量
wire [WIDTH-1:0] g; //generate变量
wire [WIDTH-1:0] p; //propagate变量
wire [WIDTH-1:0] sum_w; //用来连线传递和
reg cin_r,cout_r;
reg [WIDTH-1:0] x_r,y_r,sum_r;
//生成和
assign sum_w = p ^ c[WIDTH-1:0];
//生成进位
assign c[0] = cin_r;
assign c[WIDTH:1] = g | (c & p);
//生成PG信号
assign p = x_r ^ y_r; //生成propagate信号
assign g = x_r & y_r; //生成generate信号
//输出端口连接
assign sum = sum_r;
assign cout = cout_r;
//输入寄存
always@(posedge clk)begin
x_r <= x;
y_r <= y;
cin_r <= cin;
end
//输出寄存
always@(posedge clk)begin
sum_r <= sum_w;
cout_r <= c[WIDTH]; //最高位是输出的进位
end
endmodule分别例化4位加法,8位加法,16位加法和32位加法,记录它们的逻辑级数logic levels、最差建立时间裕量WNS和电路面积,并算出最大运行频率Fmax。如下:
| 4位 | 8位 | 16位 | 32位 | |
|---|---|---|---|---|
| WNS(ns) | 8.777 | 8.155 | 7.306 | 5.557 |
| Fmax(Mhz) | 818 | 542 | 371 | 225 |
| logic levels(级) | 2 | 4 | 7 | 13 |
| 电路面积(不考虑FF) | 4 LUT | 8 LUT | 24 LUT | 56 LUT |
从上表可以看到:
-
随着加法器位宽的增加,逻辑级数也越来越大,这是导致时序性能变差的直接原因。
-
时序性能从818M相关性地降低到180M,需要说明的是这里的最大频率Fmax只能作为一个参考,因为我整个工程只添加了这么一个加法器,而且Fmax一般还和FGPA的器件强挂钩,一般的器件肯定是跑不到800M的,这里我们主要是观察这个频率降低的趋势。
-
电路面积上是几位加法就用几个LUT
在之前的文章中,也统计了RCA电路的相关指数,这里再贴出来:
| 4位 | 8位 | 16位 | 32位 | |
|---|---|---|---|---|
| WNS(ns) | 8.777 | 8.155 | 6.917 | 4.429 |
| Fmax(Mhz) | 818 | 542 | 324 | 180 |
| logic levels(级) | 2 | 4 | 8 | 16 |
| 电路面积(不考虑FF) | 4 LUT | 8 LUT | 16 LUT | 32 LUT |
可以看到,随着位宽的增加,CLA加法器还是比RCA加法器要快一些(差距不大是因为FPGA没有门电路,都用LUT合并了很多逻辑),但是相应的其消耗的电路面积也要更多。
作为参考,接下来我们不使用任何加法器,就直接用加法运算符 + 来实现加法,电路就让综合工具vivado自动生成,看看性能如何:
| 4位 | 8位 | 16位 | 32位 | |
|---|---|---|---|---|
| WNS(ns) | 8.777 | 8.755 | 8.657 | 8.461 |
| Fmax(Mhz) | 818 | 803 | 745 | 650 |
| logic levels(级) | 2 | 3 | 5 | 9 |
| 电路面积(不考虑FF) | 4 LUT | 8 LUT + 3 CARRY4 | 16 LUT + 5 CARRY4 | 32 LUT + 9 CARRY4 |
从上表可以看到:
-
vivado综合出来的加法电路在时序性能上明显比 “假CLA” 电路要强。
-
逻辑级数的增加并没有 “假CLA” 电路那么明显,哪怕是32位的加法也只有9级逻辑层级。这也是它频率能跑很高的直接原因。
-
4位加法使用的电路面积和 “假CLA” 是一样的,因为位宽较小,综合工具直接用LUT而不是CARRY4来生成电路,二者在小位宽时的时序性能差不多
-
之所以大位宽加法的时序性能仍然比较好是因为综合工具使用CARRY4来实现加法,这种结构的加法电路有很快的进位速度,而且可以合并很多个进位链上的LUT从而减少逻辑级数
-
CARRY4的使用尽管可以提高时序性能,但是也会增大一部分电路面积。当然了,拿这点面积来换性能的提升,还是十分划算的。
如果你不了解CARRY4,可以看看这篇文章:从底层结构开始学习FPGA(7)----进位链CARRY4
或者看看这个专栏:从底层结构开始学习FPGA
5、总结
超前进位加法器CLA由于自身的门电路结构和FPGA的结构原因,导致其在FPGA设计中并没有太多作用。对于FPGA设计来说,如今的综合工具已经非常智能了,所以一般的加法还是不要自己设计加法器了,直接让综合工具生成或者用IP就行。