目录
- 一、哈希的基本概念
- (一)哈希函数的特性
- (二)哈希冲突
- 二、C++ 中的哈希表实现
- 三、哈希表的性能分析
- 四、哈希表的应用场景
- 五、优化哈希表的策略
- 六、例题讲解
- 【模板】字符串哈希
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 【一本通提高篇哈希和哈希表】乌力波(oulipo)
- [题目描述]
- 输入
- 输出
- 样例输入
- 样例输出
- 形式化题面
- 思路
- AC代码
- [POI2010] ANT-Antisymmetry
- 题目描述(翻译)
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 思路
- AC代码
- 唯一的雪花 Unique Snowflakes
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 思路
- AC代码
- [POI2010] KOR-Beads
- 题目描述
- 输入格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- AC代码
- [POI2012] OKR-A Horrible Poem
- 题面翻译
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- AC代码
- Kazaee
- 题面翻译
- 题目描述
- 输入格式
- 输出格式
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- AC代码
- 七、总结
在计算机科学领域,数据的高效存储和检索始终是一个关键问题。哈希(Hash)和哈希表(Hash Table)作为一种强大的数据结构,为解决这一问题提供了高效且灵活的方案。在这篇博客中,我们将深入探讨 C++ 中哈希和哈希表的原理、实现以及应用。
一、哈希的基本概念
哈希是一种将任意长度的输入(通常称为键)通过特定的哈希函数转换为固定长度输出(称为哈希值)的技术。
(一)哈希函数的特性
确定性:对于相同的输入,哈希函数总是产生相同的输出。
快速计算:能够在较短的时间内计算出哈希值。
分布均匀:哈希值应尽可能均匀地分布在可能的取值范围内。
例如,常见的哈希函数有简单的取余运算 hash(key) = key % tableSize ,或者更复杂的如 MurmurHash 、SHA-1 等。
(二)哈希冲突
由于哈希值的取值范围是有限的,而可能的键值数量是无限的,必然会出现不同的键通过哈希函数得到相同的哈希值,这就是哈希冲突。
解决哈希冲突的常见方法有:
开放寻址法
线性探测:当发生冲突时,依次检查下一个位置,直到找到空闲位置。
二次探测:通过特定的二次函数计算探测位置。
双重哈希:使用两个哈希函数来确定探测序列。
链地址法
在哈希表的每个位置存储一个链表,将具有相同哈希值的元素存储在该链表中。
二、C++ 中的哈希表实现
C++ 标准库中并没有提供直接的哈希表实现,但我们可以通过自定义类来实现一个简单的哈希表。
template<typename Key, typename Value>
class HashTable {
private:
// 定义哈希表的数组大小
static const int TABLE_SIZE = 100;
// 存储键值对的链表节点
struct Node {
Key key;
Value value;
Node* next;
Node(Key k, Value v) : key(k), value(v), next(nullptr) {}
};
// 哈希表数组
Node* table[TABLE_SIZE];
// 哈希函数
int hashFunction(Key key) {
// 简单的取余哈希函数示例
return std::hash<Key>{}(key) % TABLE_SIZE;
}
public:
// 插入键值对
void insert(Key key, Value value) {
int index = hashFunction(key);
Node* newNode = new Node(key, value);
if (table[index] == nullptr) {
table[index] = newNode;
} else {
Node* curr = table[index];
while (curr->next!= nullptr) {
curr = curr->next;
}
curr->next = newNode;
}
}
// 查找键对应的值
Value* search(Key key) {
int index = hashFunction(key);
Node* curr = table[index];
while (curr!= nullptr) {
if (curr->key == key) {
return &(curr->value);
}
curr = curr->next;
}
return nullptr;
}
// 删除键值对
void remove(Key key) {
int index = hashFunction(key);
Node* curr = table[index];
Node* prev = nullptr;
while (curr!= nullptr) {
if (curr->key == key) {
if (prev == nullptr) {
table[index] = curr->next;
} else {
prev->next = curr->next;
}
delete curr;
return;
}
prev = curr;
curr = curr->next;
}
}
};
如果实在懒得写哈希,也可以用set、map,它们两个的内部使用平衡树来实现的,复杂度O(logn),C++较高级的版本中提供了unodered_set、unodered_map,内部使用哈希来实现,理论复杂度为O(1)
注意:STL中的库自带一个很大的常数,而且模数公开,CF的比赛就经常卡STL中的库
三、哈希表的性能分析
平均查找时间复杂度
在理想情况下,不发生哈希冲突时,哈希表的查找时间复杂度为 O(1)。但由于哈希冲突的存在,实际平均查找时间复杂度通常接近 O(1)。
空间复杂度
哈希表的空间复杂度主要取决于存储键值对所需的空间以及解决哈希冲突所额外使用的空间。
四、哈希表的应用场景
数据库索引
加快数据的查找和检索速度。
缓存系统
存储经常访问的数据,提高系统性能。
集合和映射的实现
如 C++ 中的 unordered_set 和 unordered_map 。
五、优化哈希表的策略
选择合适的哈希函数
根据数据特点选择具有良好分布特性的哈希函数。
调整哈希表的大小
当负载因子过高时,重新调整哈希表的大小,以减少哈希冲突。
六、例题讲解
【模板】字符串哈希
题目描述
如题,给定 N N N 个字符串(第 i i i 个字符串长度为 M i M_i Mi,字符串内包含数字、大小写字母,大小写敏感),请求出 N N N 个字符串中共有多少个不同的字符串。
友情提醒:如果真的想好好练习哈希的话,请自觉。
输入格式
第一行包含一个整数 N N N,为字符串的个数。
接下来 N N N 行每行包含一个字符串,为所提供的字符串。
输出格式
输出包含一行,包含一个整数,为不同的字符串个数。
样例 #1
样例输入 #1
5
abc
aaaa
abc
abcc
12345
样例输出 #1
4
提示
对于 30 % 30\% 30% 的数据: N ≤ 10 N\leq 10 N≤10, M i ≈ 6 M_i≈6 Mi≈6, M m a x ≤ 15 Mmax\leq 15 Mmax≤15。
对于 70 % 70\% 70% 的数据: N ≤ 1000 N\leq 1000 N≤1000, M i ≈ 100 M_i≈100 Mi≈100, M m a x ≤ 150 Mmax\leq 150 Mmax≤150。
对于 100 % 100\% 100% 的数据: N ≤ 10000 N\leq 10000 N≤10000, M i ≈ 1000 M_i≈1000 Mi≈1000, M m a x ≤ 1500 Mmax\leq 1500 Mmax≤1500。
样例说明:
样例中第一个字符串(abc)和第三个字符串(abc)是一样的,所以所提供字符串的集合为{aaaa,abc,abcc,12345},故共计4个不同的字符串。
Tip:
感兴趣的话,你们可以先看一看以下三题:
BZOJ3097:http://www.lydsy.com/JudgeOnline/problem.php?id=3097
BZOJ3098:http://www.lydsy.com/JudgeOnline/problem.php?id=3098
BZOJ3099:http://www.lydsy.com/JudgeOnline/problem.php?id=3099
如果你仔细研究过了(或者至少仔细看过AC人数的话),我想你一定会明白字符串哈希的正确姿势的_
思路
常用的对字符串的哈希方式是进制哈希。也就是设一个 base,其中 base > 字符集 Σ。然后将整个字符串看成是一个 base 进制的整数,并且对一个模数取模,就能支持上述的两种操作。
当两个不同数据加密结果相同时称为哈希冲突。为了减少冲突一般将 base 设为一个较大的质数,如 13331。模数也要是更大的质数,例如 109+7、109+9 等。
对于每个字符串,我们可以将它看做一个26进制的整数,A代表0,B代表1……
然后26进制转十进制,即为它的哈希值
AC代码
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef unsigned long long ull;
ull base=131;
ull a[10010];
char s[10010];
int n,ans=1;
int prime=233317;
ull mod=212370440130137957ll;
ull hashe(char s[])
{
int len=strlen(s);
ull ans=0;
for (int i=0;i<len;i++)
ans=(ans*base+(ull)s[i])%mod+prime;
return ans;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%s",s);
a[i]=hashe(s);
}
sort(a+1,a+n+1);
for(int i=1;i<n;i++)
{
if(a[i]!=a[i+1])
ans++;
}
printf("%d",ans);
}
【一本通提高篇哈希和哈希表】乌力波(oulipo)
[题目描述]
法国作家乔治·佩雷克(Georges Perec,1936-1982)曾经写过一本书,《敏感字母》(La disparition),全篇没有一个字母‘e’。他是乌力波小组(Oulipo Group)的一员。下面是他书中的一段话:
Tout avait Pair normal, mais tout s’affirmait faux. Tout avait Fair normal, d’abord, puis surgissait l’inhumain, l’affolant. Il aurait voulu savoir où s’articulait l’association qui l’unissait au roman : stir son tapis, assaillant à tout instant son imagination, l’intuition d’un tabou, la vision d’un mal obscur, d’un quoi vacant, d’un non-dit : la vision, l’avision d’un oubli commandant tout, où s’abolissait la raison : tout avait l’air normal mais…
佩雷克很可能在下面的比赛中得到高分(当然,也有可能是低分)。在这个比赛中,人们被要求针对一个主题写出甚至是意味深长的文章,并且让一个给定的“单词”出现次数尽量少。我们的任务是给评委会编写一个程序来数单词出现了几次,用以得出参赛者最终的排名。参赛者经常会写一长串废话,例如500000个连续的‘T’。并且他们不用空格。
因此我们想要尽快找到一个单词出现的频数,即一个给定的字符串在文章中出现了几次。更加正式地,给出字母表{‘A’,‘B’,‘C’,…,‘Z’}和两个仅有字母表中字母组成的有限字符串:单词W和文章T,找到W在T中出现的次数。这里“出现”意味着W中所有的连续字符都必须对应T中的连续字符。T中出现的两个W可能会部分重叠。
输入
输入包含多组数据。
输入文件的第一行有一个整数,代表数据组数。接下来是这些数据,以如下格式给出:
第一行是单词W,一个由{‘A’,‘B’,‘C’,…,‘Z’}中字母组成的字符串,保证1<=|W|<=10000(|W|代表字符串W的长度)
第二行是文章T,一个由{‘A’,‘B’,‘C’,…,‘Z’}中字母组成的字符串,保证|W|<=|T|<=1000000。
输出
对每组数据输出一行一个整数,即W在T中出现的次数。
样例输入
3
BAPC
BAPC
AZA
AZAZAZA
VERDI
AVERDXIVYERDIAN
样例输出
1
3
0
形式化题面
多组数据,每组数据输入两个字符串 W 和 T,求 W 在 T 中的出现次数,1≤|W|≤10000, 1≤|T|<=10^6。
思路
板子题,直接按刚才说的实现就行了。
AC代码
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ULL;
const int N=1e6+5,P=131;
ULL h[N],p[N],hh[N];
int t,ans;
ULL query(int l,int r,ULL h[]){
return h[r]-h[l-1]*p[r-l+1];
}
int main()
{
cin>>t;
while(t--)
{
string x,y;
cin>>x>>y;
p[0]=1;
h[0]=0;
hh[0]=0;
for(int i=0;i<x.size();i++)
{
p[i+1]=p[i]*P;
h[i+1]=h[i]*P+x[i];
}
for(int i=0;i<y.size();i++)
{
hh[i+1]=hh[i]*P+y[i];
}
for(int i=0;i+x.size()<=y.size();i++)
{
if(query(i+1,i+x.size(),hh)==query(1,x.size(),h)) ans++;
}
cout<<ans<<endl;
ans=0;
}
return 0;
}
[POI2010] ANT-Antisymmetry
题目描述(翻译)
对于一个01字符串,如果将这个字符串0和1取反后,再将整个串反过来和原串一样,就称作“反对称”字符串。比如00001111和010101就是反对称的,1001就不是。
现在给出一个长度为N的01字符串,求它有多少个子串是反对称的。
输入格式

输出格式
The first and only line of the standard output should contain a single integer, namely the number of contiguous (non empty) fragments of the given string that are antisymmetric.
样例 #1
样例输入 #1
8
11001011
样例输出 #1
7
提示
7个反对称子串分别是:01(出现两次),10(出现两次),0101,1100和001011
n ≤ 5 × 1 0 5 n \le 5 \times 10^5 n≤5×105
思路
考虑枚举反对称字符串的对称中心。
这样的话就可以把问题转化成从每个对称中心向外拓展,能拓展出多少个反对称子串。
而我们可以注意到,这样的拓展是有单调性的,也就是如果左右拓展 i+1 位是反对称子串,那么拓展 i 位一定也是反对称子串。
于是就可以二分,二分之后用哈希来判断是否是反对称的。
注意对称中心可能是一个字符或者两个字符中间,需要分别处理。
AC代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#define N 500010
#define ll unsigned long long
using namespace std;
template<typename T>
inline void read(T &x)
{
x=0;char c = getchar();int s = 1;
while(c < '0' || c > '9') {
if(c == '-') s = -1;
c = getchar();
}
while(c >= '0' && c <= '9') {
x = x*10 + c -'0';
c = getchar();
}
x*=s;
}
int n,base=13331,bas[N],has[N],_has[N];
ll ans;
char s[N];
ll inline gethash(int l,int r){
return has[r]-has[l-1]*bas[r-l+1];
}
inline ll _gethash(int l,int r){
return _has[l]-_has[r+1]*bas[r-l+1];
}
inline bool check(int l,int r){
if(l>r)return false;
return gethash(l,r)==_gethash(l,r);
}
int main(){
read(n);
scanf("%s",s+1);
bas[0]=1;
for(int i=1;i<=n;i++)
bas[i]=bas[i-1]*base;
for(int i=1;i<=n;i++)
has[i]=has[i-1]*base+s[i]-'0';
for(int i=n;i;i--)
_has[i]=_has[i+1]*base+((s[i]-'0')^1);
for(int i=1;i<n;i++){
int l=1,r=min(n-i,i),mid,res=0;
while(l<=r){
mid=l+r>>1;
if(check(i-mid+1,i+mid))l=mid+1,res=mid;
else r=mid-1;
}
ans+=res;
}
for(int i=2;i<n;i++){
int l=1,r=min(n-i,i-1),mid,res=0;
while(l<=r){
mid=l+r>>1;
if(check(i-mid+1,i+mid-1))l=mid+1,res=mid;
else r=mid-1;
}
ans+=res;
}
printf("%llu\n",ans);
return 0;
}
唯一的雪花 Unique Snowflakes
题面翻译
【题目描述】
企业家 Emily 有一个很酷的主意:把雪花包起来卖。她发明了一台机器,这台机器可以捕捉飘落的雪花,并把它们一片一片打包进一个包裹里。一旦这个包裹满了,它就会被封上送去发售。
Emily 的公司的口号是“把独特打包起来”,为了实现这一诺言,一个包裹里不能有两片一样的雪花。不幸的是,这并不容易做到,因为实际上通过机器的雪花中有很多是相同的。Emily 想知道这样一个不包含两片一样的雪花的包裹最大能有多大,她可以在任何时候启动机器,但是一旦机器启动了,直到包裹被封上为止,所有通过机器的雪花都必须被打包进这个包裹里,当然,包裹可以在任何时候被封上。
【输入格式】
第一行是测试数据组数 T T T,对于每一组数据,第一行是通过机器的雪花总数 n n n( n ≤ 10 6 n \le {10}^6 n≤106),下面 n n n 行每行一个在 [ 0 , 10 9 ] [0, {10}^9] [0,109] 内的整数,标记了这片雪花,当两片雪花标记相同时,这两片雪花是一样的。
【输出格式】
对于每一组数据,输出最大包裹的大小。
题目描述

输入格式
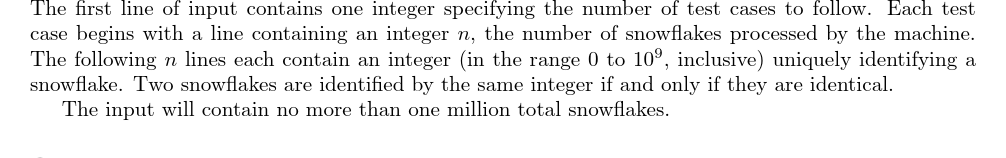
输出格式
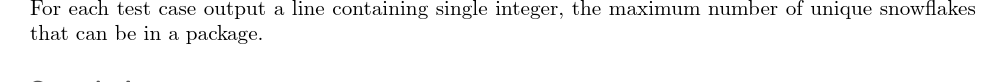
样例 #1
样例输入 #1
1
5
1
2
3
2
1
样例输出 #1
3
思路
本题有多种做法,此处只展示一种
AC代码
#include<bits/stdc++.h>
using namespace std;
map<int,int> snow;
int T,n,ans,last,a;
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>T;
while(T--)
{
snow.clear();
cin>>n;
last=ans=0;
for(int i=1;i<=n;i++)
{
cin>>a;
if(snow[a]>last)last=snow[a];
ans=max(ans,i-last);
snow[a]=i;
}
cout<<ans<<endl;
}
return 0;
}
[POI2010] KOR-Beads
题目描述
Zxl有一次决定制造一条项链,她以非常便宜的价格买了一长条鲜艳的珊瑚珠子,她现在也有一个机器,能把这条珠子切成很多块(子串),每块有k(k>0)个珠子,如果这条珠子的长度不是k的倍数,最后一块小于k的就不要拉(nc真浪费),保证珠子的长度为正整数。 Zxl喜欢多样的项链,为她应该怎样选择数字k来尽可能得到更多的不同的子串感到好奇,子串都是可以反转的,换句话说,子串(1,2,3)和(3,2,1)是一样的。写一个程序,为Zxl决定最适合的k从而获得最多不同的子串。 例如:这一串珠子是: (1,1,1,2,2,2,3,3,3,1,2,3,3,1,2,2,1,3,3,2,1), k=1的时候,我们得到3个不同的子串: (1),(2),(3) k=2的时候,我们得到6个不同的子串: (1,1),(1,2),(2,2),(3,3),(3,1),(2,3) k=3的时候,我们得到5个不同的子串: (1,1,1),(2,2,2),(3,3,3),(1,2,3),(3,1,2) k=4的时候,我们得到5个不同的子串: (1,1,1,2),(2,2,3,3),(3,1,2,3),(3,1,2,2),(1,3,3,2)
输入格式
输出两行,第一行第一个数为最多可以得到的不同子串的个数,第二个数为取到最优解时的不同的k的个数。第二行包含若干个数,为取到最优解时的不同的k 。第二行中的不同的k可以按任意位置输出。
样例 #1
样例输入 #1
21
1 1 1 2 2 2 3 3 3 1 2 3 3 1 2 2 1 3 3 2 1
样例输出 #1
6 1
2
提示
1 ≤ n ≤ 2 × 1 0 5 1≤n≤2\times 10^5 1≤n≤2×105,且 ∀ 1 ≤ i ≤ n \forall 1\le i\le n ∀1≤i≤n,有 1 ≤ a i ≤ n 1\le a_i\le n 1≤ai≤n
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll base=1e9+7;
struct node{
int ans,seat;
}q[300010];
int s[200010];
ll a[200010],sum[200010],num[200010];
ll res,cnt;
set<ll> S;
bool cmp(node x,node y)
{
if(x.ans==y.ans)
return x.seat<y.seat;
return x.ans>y.ans;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
ll i,j,k,n,m;
cin>>n;
for(i=1;i<=n;i++)cin>>s[i];
a[0]=1;
for(i=1;i<=n;i++)a[i]=a[i-1]*base;
for(i=1;i<=n;i++)sum[i]=sum[i-1]*base+s[i];
for(i=n;i>=1;i--)num[i]=num[i+1]*base+s[i];
m=n;
for(k=1;k<=m;k++)
{
res=0;
for(j=k;j<=n;j+=k)
{
ll t1=sum[j]-sum[j-k]*a[k];
ll t2=num[j-k+1]-num[j+1]*a[k];
ll t3=t1*t2;
if(S.count(t3))continue;
S.insert(t3);
res++;
}
if(res!=0)
{
m=min(m,n/res);
q[++cnt].ans=res;
q[cnt].seat=k;
}
}
sort(q+1,q+1+cnt,cmp);
for(i=2;i<=cnt;i++)
if(q[i].ans!=q[i-1].ans)
break;
cout<<q[1].ans<<" "<<i-1<<endl;
for(j=1;j<i;j++)
cout<<q[j].seat<<" ";
return 0;
}
[POI2012] OKR-A Horrible Poem
题面翻译
给出一个由小写英文字母组成的字符串 S S S,再给出 q q q 个询问,要求回答 S S S 某个子串的最短循环节。
如果字符串 B B B 是字符串 A A A 的循环节,那么 A A A 可以由 B B B 重复若干次得到。
第一行一个正整数 n ( n ≤ 5 × 1 0 5 ) n\ (n\le 5\times 10^5) n (n≤5×105),表示 S S S 的长度。
第二行 n n n 个小写英文字母,表示字符串 S S S。
第三行一个正整数 q ( q ≤ 2 × 1 0 6 ) q\ (q\le 2\times 10^6) q (q≤2×106),表示询问次数。
下面 q q q 行每行两个正整数 a , b ( 1 ≤ a ≤ b ≤ n ) a,b(1\le a\le b\le n) a,b(1≤a≤b≤n),表示询问字符串 S [ a ⋯ b ] S[a\cdots b] S[a⋯b] 的最短循环节长度。
样例 #1
样例输入 #1
8
aaabcabc
3
1 3
3 8
4 8
样例输出 #1
1
3
5
AC代码
#include <cstdio>
#include <cctype>
#include <vector>
using namespace std;
template<typename T>
inline void read(T &x) {
x = 0; T k = 1; char in = getchar();
while (!isdigit(in)) { if (in == '-') k = -1; in = getchar(); }
while (isdigit(in)) x = x * 10 + in - '0', in = getchar();
x *= k;
}
typedef long long ll;
const ll MOD = 1e9 + 7;
const int N = 5e5 + 5;
int n, m;
ll g[N], has[N], power[N];
char s[N];
bool vis[N];
vector<ll> pri;
inline void euler() {
for (ll i = 2; i <= n; ++i) {
if (!vis[i])
pri.push_back(i), g[i] = i;
for (int j = 0; j < pri.size() && pri[j] * i <= n; ++j) {
vis[pri[j]*i] = true, g[pri[j]*i] = pri[j];
if (i % pri[j] == 0)
break;
}
}
}
inline ll calc(int l, int r) {
return ((has[r] - has[l-1] * power[r-l+1]) % MOD + MOD) % MOD;
}
int main() {
read(n);
euler();
scanf("%s", s+1);
for (int i = 1; i <= n; ++i)
has[i] = (has[i-1] * 29 + s[i] - 'a' + 1) % MOD;
power[0] = 1;
for (int i = 1; i <= n; ++i)
power[i] = (power[i-1] * 29) % MOD;
read(m);
while (m--) {
int l, r, len, ans;
read(l), read(r), ans = len = r - l + 1;
if (calc(l+1, r) == calc(l, r-1)) {
puts("1");
continue;
}
while (len > 1) {
if (calc(l+ans/g[len], r) == calc(l, r-ans/g[len]))
ans /= g[len];
len /= g[len];
}
printf("%d\n", ans);
}
return 0;
}
一个小技巧,模数在开头用const int 定义成常量,会有取模优化,加快程序运行效率
Kazaee
题面翻译
题目描述
给出一个长度为 n n n 的数组 a a a 和以下两种操作:
- 1 i x 1\ i\ x 1 i x:将 a i a_i ai 修改为 x x x。
-
2
l
r
k
2\ l\ r\ k
2 l r k:询问在数组区间
[
l
,
r
]
[l, r]
[l,r] 内是否每个出现过的正整数的出现次数都是
k
k
k 的倍数。(建议参照样例理解)若是则输出
YES,若否则输出NO。
输入格式
第一行两个整数 n n n、 q q q,表示数组长度和操作数。
第二行 n n n 个整数,为数组 a a a 中的元素。(下标从1开始)
之后 q q q 行,每行一个询问。
输出格式
对于每个操作2,给出相应答案(YES 或 NO)。
题目描述
You have an array $ a $ consisting of $ n $ positive integers and you have to handle $ q $ queries of the following types:
- $ 1 $ $ i $ $ x $ : change $ a_{i} $ to $ x $ ,
- $ 2 $ $ l $ $ r $ $ k $ : check if the number of occurrences of every positive integer in the subarray $ a_{l}, a_{l+1}, \ldots a_{r} $ is a multiple of $ k $ (check the example for better understanding).
输入格式
The first line of the input contains two integers $ n $ and $ q $ ( $ 1 \le n , q \le 3 \cdot 10^5 $ ), the length of $ a $ and the number of queries.
Next line contains $ n $ integers $ a_{1}, a_{2}, \ldots a_{n} $ ( $ 1 \le a_{i} \le 10^9 $ ) — the elements of $ a $ .
Each of the next $ q $ lines describes a query. It has one of the following forms.
- $ 1 $ $ i $ $ x $ , ( $ 1 \le i \le n $ , $ 1 \le x \le 10^9 $ ), or
- $ 2 $ $ l $ $ r $ $ k $ , ( $ 1 \le l \le r \le n $ , $ 1 \le k \le n $ ).
输出格式
For each query of the second type, if answer of the query is yes, print “YES”, otherwise print “NO”.
样例 #1
样例输入 #1
10 8
1234 2 3 3 2 1 1 2 3 4
2 1 6 2
1 1 1
2 1 6 2
2 1 9 2
1 10 5
2 1 9 3
1 3 5
2 3 10 2
样例输出 #1
NO
YES
NO
YES
YES
提示
In the first query, requested subarray is $ [1234, 2, 3, 3, 2, 1] $ , and it’s obvious that the number of occurrence of $ 1 $ isn’t divisible by $ k = 2 $ . So the answer is “NO”.
In the third query, requested subarray is $ [1, 2, 3, 3, 2, 1] $ , and it can be seen that the number of occurrence of every integer in this sub array is divisible by $ k = 2 $ . So the answer is “YES”.
In the sixth query, requested subarray is $ [1, 2, 3, 3, 2, 1, 1, 2, 3] $ , and it can be seen that the number of occurrence of every integer in this sub array is divisible by $ k = 3 $ . So the answer is “YES”.
AC代码
#include <iostream>
#include <cmath>
#include <random>
#include <ctime>
#include <algorithm>
#include <cstring>
using namespace std;
std::mt19937 rnd(time(0));
#define maxn 300010
#define LL long long
int n, Q;
LL tree[maxn << 1];
LL a[maxn], Hash[maxn << 1], b[maxn];
int ans[maxn];
struct node
{
int val, id;
} num[maxn << 1];
struct Ques
{
int opt, l, r, val;
} q[maxn];
inline bool cmp(node x, node y)
{
return x.val < y.val;
}
inline int lowbit(int k)
{
return k & -k;
}
inline void update(int x, LL delta)
{
for (; x <= n; x += lowbit(x))
tree[x] += delta;
}
inline LL query(int x)
{
LL sum = 0;
if (x == 0) return 0;
for (; x; x -= lowbit(x))
sum += tree[x];
return sum;
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>Q;
int cnt_num = n;
for (int i = 1; i <= n; ++i)
{
cin>>a[i];
num[i].val = a[i];
num[i].id = i;
}
for (int i = 1; i <= Q; ++i)
{
cin>>q[i].opt;
if (q[i].opt == 1)
{
cin>>q[i].l>>q[i].val;
num[++cnt_num].val = q[i].val;
num[cnt_num].id = n + i;
}
else
cin>>q[i].l>>q[i].r>>q[i].val;
}
sort(num + 1, num + 1 + cnt_num, cmp);
num[0].val = num[1].val - 1;
int p = 0;
for (int i = 1; i <= cnt_num; ++i)
{
if (num[i].val != num[i - 1].val)p++;
if (num[i].id <= n)a[num[i].id] = p;
else q[num[i].id - n].val = p;
}
for (int i = 1; i <= n; ++i)b[i] = a[i];
for (int i = 1; i <= Q; ++i)ans[i] = 1;
for (int times = 1; times <= 30; ++times)
{
memset(tree, 0, sizeof(tree));
for (int i = 1; i <= n; ++i)a[i] = b[i];
for (int i = 1; i <= p; ++i)Hash[i] = rnd();
for (int i = 1; i <= n; ++i)update(i, Hash[a[i]]);
for (int i = 1; i <= Q; ++i)
{
if (q[i].opt == 1)
{
int pos = q[i].l;
update(pos, Hash[q[i].val] - Hash[a[pos]]);
a[pos] = q[i].val;
}
else if (ans[i])
{
LL sum = query(q[i].r) - query(q[i].l - 1);
if (sum % q[i].val != 0)
ans[i] = 0;
}
}
}
for (int i = 1; i <= Q; ++i)
if (q[i].opt == 2)
if (ans[i])
puts("YES");
else
puts("NO");
return 0;
}
七、总结
哈希和哈希表是 C++ 编程中非常重要的数据结构,它们在提高数据存储和检索效率方面发挥着关键作用。通过深入理解其原理和实现,我们能够在实际编程中更好地运用它们来解决各种问题。
这是我的第十六篇文章,如有纰漏也请各位大佬指正
辛苦创作不易,还望看官点赞收藏打赏,后续还会更新新的内容。


![C语言程序设计-[3] 运算符和表达式](https://i-blog.csdnimg.cn/direct/afa65165b7bf435ea2411f47cee7c08a.png)