目录
1、前言
2、半减器
3、全减器
4、减法器
文章总目录点这里:《基于FPGA的数字信号处理》专栏的导航与说明
1、前言
既然有半加器和全加器,那自然也有半减器和全减器了。尽管在电路中减法的实现基本都是 补码 + 加法 的形式,但是正所谓技多不压身,了解一下半减器和全减器还是有一定作用的,至少能扩宽知识面嘛。
2、半减器
最简单的减法器叫做 半减器(Half Subtractor),它将2个1bit的输入数据相减,输出一个1bit的结果即 差Di(Difference),以及向高位的借位Bo(Borrow output)。例如:
-
1 - 1 = 01 -1 = 0,不需要向高位借位,差为0,即Bo = 0,Di = 0
-
1 - 0 = 01 -0 = 1,不需要向高位借位,差为1,即Bo = 0,Di = 1
-
0 - 1 = 10 -1 = 1, 需要向高位借位,差为1,即Bo = 1,Di = 1
-
0 - 0 = 00 -0 = 0,不需要向高位借位,差为0,即Bo = 0,Di = 0
2个1bit数相减,最多只有4种情况(在上面已经例出来了),据此可以写出半减器的真值表:
| 被减数 | 减数 | 差 | 向高位借位 |
|---|---|---|---|
| X | Y | Di | Bo |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
从这个真值表,不难推断出输出的逻辑表达式:
-
差Di在2个输入不同时为1,所以它是输入异或的结果,即 Di = a ^ b
-
向高位借位Bo在X = 0 且 Y = 1 时才为1,即 Bo= ~X & Y
有了逻辑表达式后,可以很容易地画出对应的门电路结构:
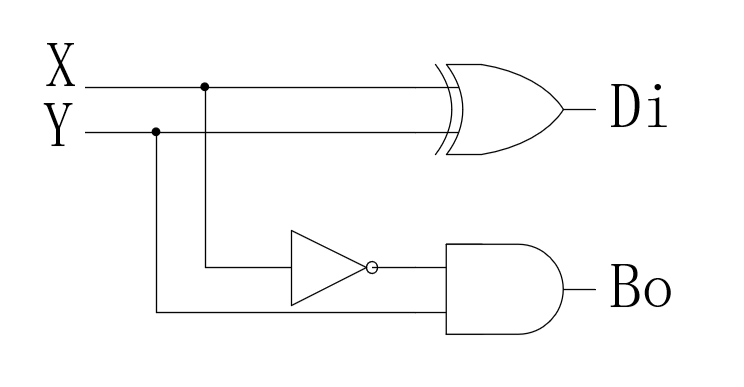
顺便提一句,虽然半减器的基本电路是上面这个样子的,但是因为在FPGA中只有查找表LUT而没有具体的门电路,所以如果用FPGA来综合半减器的话,它的电路应该是这个样子的(因为只有2个输入和2个输出,所以只要1个LUT6就可以覆盖到所有情况):
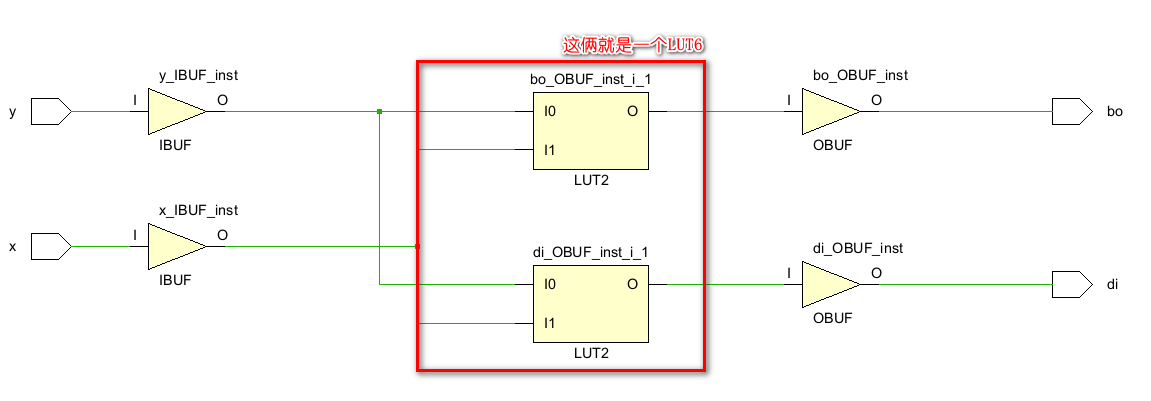
如果你不了解LUT,可以看看这篇文章:从底层结构开始学习FPGA(2)----LUT查找表,或者看看这个专栏:从底层结构开始学习FPGA
IBUF和OBUF是Vivado自动添加的对输入输出管脚的缓冲,尽管上图显示的是2个LUT2(可能这样的显示更清晰一点),但是实际上就是1个LUT6,下面的资源显示情况也证明了这一点:

用verilog实现半减器如下:
//使用逻辑表达式来描述半减器
module half_subtractor(
input x, //被减数
input y, //减数
output di, //差
output bo //向高位借位
);
//根据化简结果分别表示:差 与 向高位借位
assign di = x ^ y;
assign bo = ~x & y;
endmodule有了RTL,接下来就该要写个对应的TB来测试电路功能是否正常。由于这个电路足够简单(一共只有4种情况),所以我们可以把所有可能的情况都穷举出来,然后观察输出是否符合预期即可。TB如下:
`timescale 1ns/1ns //时间刻度:单位1ns,精度1ns
module tb_half_subtractor();
//定义变量
reg x;
reg y;
wire di;
wire bo;
//设置初始化条件
initial begin
//第1种情况
x =1'b0;
y =1'b0;
#10
//第2种情况
x =1'b0;
y =1'b1;
#10
//第3种情况
x =1'b1;
y =1'b0;
#10
//第4种情况
x =1'b1;
y =1'b1;
#10 $stop(); //结束仿真
end
//例化被测试模块
half_subtractor u_half_subtractor(
.x (x),
.y (y),
.di (di),
.bo (bo)
);
endmodule仿真结果如下:

通过和真值表的对比(或者验证逻辑表达式也可以),可以发现,电路的输出是符合预期的。
3、全减器
虽然半减器可以实现2个1bit数的减法,但在实际应用中,更常见的是要实现2个多bits数的减法,那么该如何实现?以2个2bits数的减法为例:
-
先把低位和高位的减法先分开。
-
低位是2个1bit的减法,所以可以用1个HS(半减器)来实现,它产生的差就是最终结果的低位,它产生的向高位借位要被送入到高位参与它们的减法。
-
高位除了要计算减数和被减数的高位外,还有1个来自低位的借位。
好,现在问题是半减器没有设计来自低位的借位,所以它处理不了这种情况。为此,全减器被设计出来了,它在半减器的基础上,增加了来自低位的借位输入。这样多个全减器就可以级联起来实现多bits的减法了。
全减器(Full Subtractor),它处理2个1bit的输入和来自低位的借位Bi(Borrow input)输入共3个数,输出一个差Di和向高位的借位Bi。例如(格式:被减数- 减数 - 来自低位的借位):
-
1 - 1 - 1 = 11 - 1 - 1 = 0,来自低位的借位为1, 需要向高位借位,差为0,即Bi = 1,Bo = 0,Di = 0
-
1 - 1 - 0 = 01 - 1 - 0 = 0,来自低位的借位为0,不需要向高位借位,差为0,即Bi = 0,Bo = 0,Di = 0
-
1 - 0 - 1 = 01 - 0 - 1 = 0,来自低位的借位为1,不需要向高位借位,差为0,即Bi = 1,Bo = 0,Di = 0
-
1 - 0 - 0 = 01 - 0 - 0 = 0,来自低位的借位为0,不需要向高位借位,差为1,即Bi = 0,Bo = 0,Di = 1
-
······
3个输入一共只有8种情况,把所有情况都穷举出来,就可以列出全减器的真值表:
| 被减数 | 减数 | 来自低位的借位 | 差 | 向高位的借位 |
|---|---|---|---|---|
| X | Y | Bi | Di | Bo |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
从这个真值表,不难推断出两个输出的逻辑表达式:
-
Di为1的4种情况,~x&~y&bi + ~x&y&~bi + x&~y&~bi + x&y&bi=~x&(~y&bi+y&~bi)+x&(~y&~bi+y&bi) = ~x&(y^bi) + x&~(y^bi) = x ^ y ^ bi
-
Bo为1的4种情况,~x&~y&bi + ~x&y&~bi + ~x&y&bi + x&y&bi = ~x&(~y&bi+y&~bi) + (~x+x)&y&bi = ~x&(y^bi) + y&bi
有了逻辑表达式后,就很容易画出电路图了(偷了个懒,不是画的,是用vivado生成的):
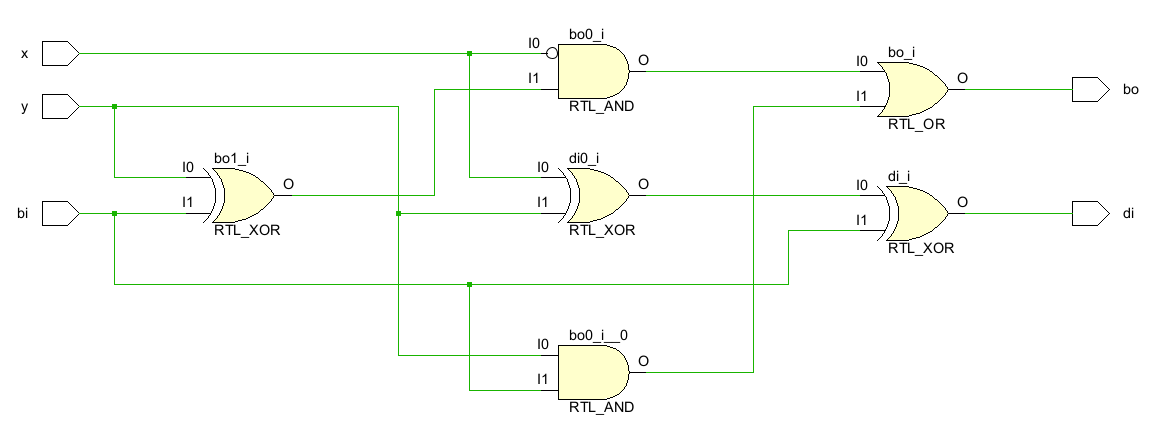
根据门电路,可以写出全减器的Verilog实现:
//使用逻辑表达式来描述全减器
module full_subtractor(
input x, //被减数
input y, //减数
input bi, //来自低位的借位
output di, //差
output bo //向高位借位
);
//根据化简结果分别表示:差 与 向高位借位
assign di = x ^ y ^ bi;
assign bo = ~x & (y ^ bi) | y & bi;
endmodule 接下来写个TB测试电路,输入一共只有8个,所以依然用穷举法来测试:
`timescale 1ns/1ns //时间刻度:单位1ns,精度1ns
module tb_full_subtractor();
//定义变量
reg x;
reg y;
reg bi;
wire di;
wire bo;
//设置初始化条件
initial begin
//第1种情况
x =1'b0;
y =1'b0;
bi =1'b0;
#10
//第2种情况
x =1'b0;
y =1'b1;
bi =1'b0;
#10
//第3种情况
x =1'b1;
y =1'b0;
bi =1'b0;
#10
//第4种情况
x =1'b1;
y =1'b1;
bi =1'b0;
#10
//第5种情况
x =1'b0;
y =1'b0;
bi =1'b1;
#10
//第6种情况
x =1'b0;
y =1'b1;
bi =1'b1;
#10
//第7种情况
x =1'b1;
y =1'b0;
bi =1'b1;
#10
//第8种情况
x =1'b1;
y =1'b1;
bi =1'b1;
#10 $stop(); //结束仿真
end
//例化被测试模块
full_subtractor u_full_subtractor(
.x (x),
.y (y),
.di (di),
.bi (bi),
.bo (bo)
);
endmodule![]()
仿真结果如下所示:
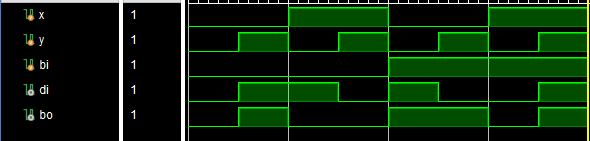
通过和真值表的对比(或者验证逻辑表达式也可以),可以发现,电路的输出是符合预期的。
4、减法器
有了全减器后,就可以实现两个多bits数的减法了,这样的电路也被称为减法器。和行波进位加法器的结构类似,我们也可以将多个全减器级联起来搭建减法器,以4bits的减法为例,它的结构如下:
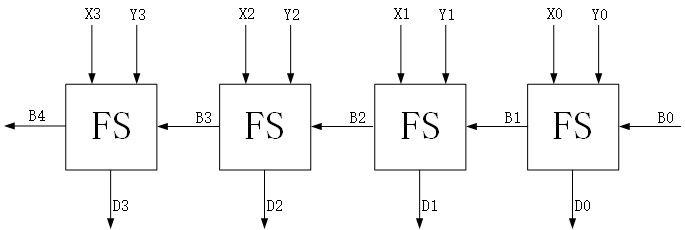
根据结构图,可以很快地写出它对应的Verilog代码:
//使用多个全减器建联构建减法器
module subtractor(
input [3:0] x, //被减数
input [3:0] y, //减数
input bi, //来自低位的借位
output [3:0] di, //差
output bo //向高位借位
);
wire b1,b2,b3; //借位连接
//例化全减器来构建减法器
full_subtractor u0(
.x (x[0]),
.y (y[0]),
.di (di[0]),
.bi (bi),
.bo (b1)
);
full_subtractor u1(
.x (x[1]),
.y (y[1]),
.di (di[1]),
.bi (b1),
.bo (b2)
);
full_subtractor u2(
.x (x[2]),
.y (y[2]),
.di (di[2]),
.bi (b2),
.bo (b3)
);
full_subtractor u3(
.x (x[3]),
.y (y[3]),
.di (di[3]),
.bi (b3),
.bo (bo)
);
endmodule这里记得要把之前的全减器也添加进工程。生成的示意图如下(这个排布不能很好地看出来层次结构,但确实没错):
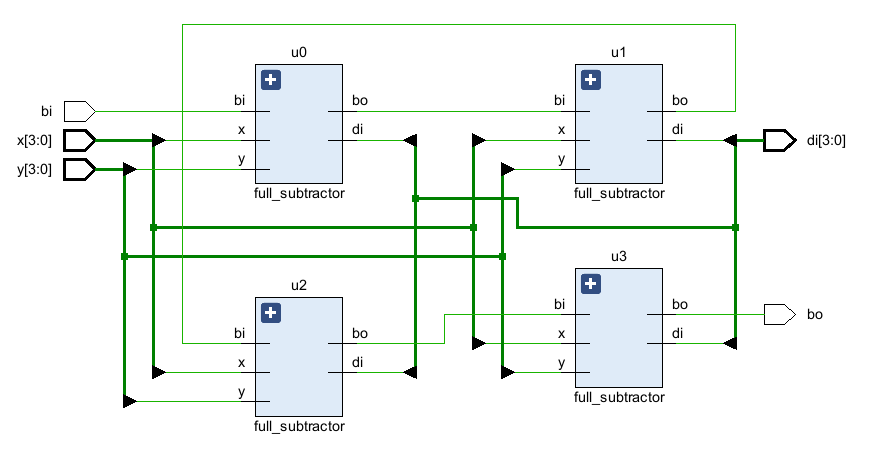
然后写个TB测试一下这个减法器电路,因为4个bits即16×16=256种情况,加上低位借位的两种情况,也才256×2=512种情况,所以依然用穷举法来测试:
`timescale 1ns/1ns //时间刻度:单位1ns,精度1ns
module tb_full_subtractor();
//定义变量
reg [3:0] x; //被减数
reg [3:0] y; //减数
reg bi; //来自低位的借位
wire [3:0] di; //差
wire bo; //向高位借位
reg [3:0] di_real; //差的真实值,作为对比
reg bo_real; //向高位借位的真实值,作为对比
wire di_flag; //di正确标志信号
wire bo_flag; //bo正确标志信号
assign di_flag = di == di_real; //di结果正确时拉高该信号
assign bo_flag = bo == bo_real; //bo结果正确时拉高该信号
integer z,i,j; //循环变量
//设置初始化条件
initial begin
//初始化
x =1'b0;
y =1'b0;
bi =1'b0; //设定低位借位为0
//穷举所有情况
for(z=0;z<=1;z=z+1)begin
bi = z;
for(i=0;i<16;i=i+1)begin
x = i;
for(j=0;j<16;j=j+1)begin
y = j;
if((i-j-z)<0)begin //减法结果是负数
di_real = (i - j - z)+ 5'd16; //加上向高位的借位
bo_real = 1; //向高位的借位为1
end
else begin //减法结果是正数数
di_real = i - j - z; //结果就是减法本身
bo_real = 0; //向高位的借位为0
end
#5;
end
end
end
#10 $stop(); //结束仿真
end
//例化被测试模块
subtractor u_subtractor(
.x (x),
.y (y),
.di (di),
.bi (bi),
.bo (bo)
);
endmoduleTB中分别用3个嵌套循环将所有情况穷举出来,即bi=0~1、x=0~15和y=0~15的所有情况。减法运算的预期结果也是很容易就可以找出来的,就是直接写减法就行。接着构建了两个标志向量di_flag和bo_flag作为电路输出与预期结果的对比值,当二者一致时即拉高这两个信号。这样我们只要观察这两个信号,即可知道电路输出是否正确。仿真结果如下:
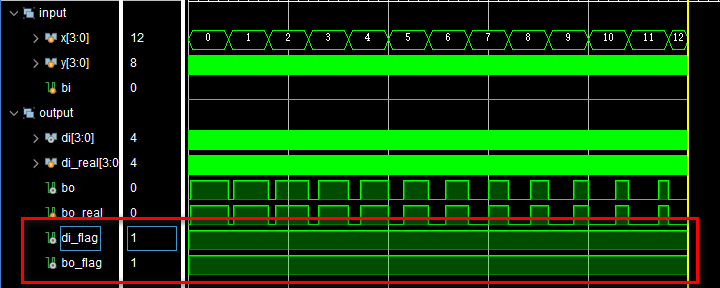
可以看到,di_flag和bo_flag都是一直拉高的,说明电路输出正确。