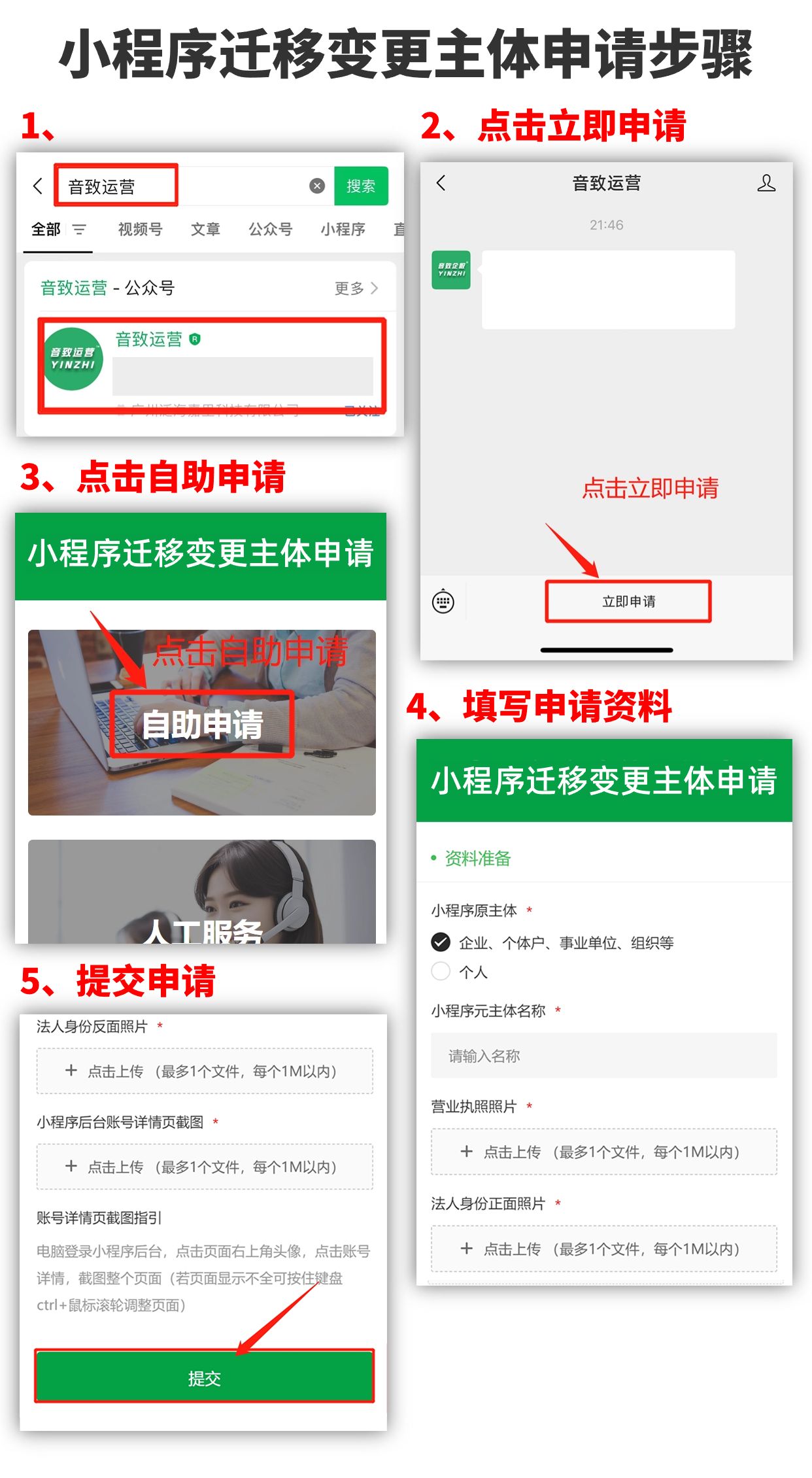
论网络流--新手入门超详解--包教包会
- 1 前言
- 2 什么是最大流
- 3最大流问题的求解
- (1)问题转化--增广路的引入
- (2)走回头路--EK算法
- (3)EK的弊端
- (4)化图为树--DINIC算法
- 4后记
1 前言
网络流是图论算法,阅读本文需要以下前置知识
1搜索算法(dfs+bfs)
2图的存储
3最短路径算法(dijkstra,floyd,spfa)
所有数学公式均使用Latex并附有证明
作为网络流系列的第一张,我们从网络流的基础–最大流开始
2 什么是最大流
我们把网络流这个词拆开来看
网络,指的就是图,在网络流问题中大多为有向图,而且有边权(容量)
流,顾名思义,就是向水一样,从一个水源(源点)流出,流向终点(汇点)
那么会有多少水流向终点呢?这就是流量
这么说肯定不好理解,我们从图的最简单形态–链出发
上图片

可以把源点看做自来水厂,汇点看做你家,中间的点就是中转站,边就是水管,水管当然不是无限大的,肯定会有容量(即边权,图上用蓝色数字标出)
假设你需要
1
1
1个单位的水,自来水厂给你供水,每个水管中流的水量在下图中用绿色标注

显然,每个水管中的水量都小于容量,水管指定炸不了
流量为
1
1
1,即你最后收到了
1
1
1个单位的水
流量可以达到
1
1
1,没有任何一个水管炸掉,这就是可行流
但是这个没啥用…流量为
0
0
0还是可行流呢
我们考虑对于一个所有可行流的集合,求其中流量最大的一个
对于这张图,答案显然了,流量为2,在下图中用橙色标出
可以看到容量为
2
2
2的水管装满水了,不能再多了,这就是最大流
3最大流问题的求解
(1)问题转化–增广路的引入
假设图是一条链,答案肯定为容量最小边的容量,要不然就炸了
但是如果图不是一条链呢
我们把图变成链不就好了
在图上取一条路径,不就形成了链吗
我们还是举上面的例子,自来水厂给你家供水,肯定是选取一条路径将水送到你家,但是如果不够用,自来水厂就会再选取一条路径给你家供水
这就是增广路–一条连接源点和汇点,且流量未满的路径
假设现在已经找到了一条增广路,我们该怎么更新
根据上面的例子,自来水厂把水送到你家,肯定占用了水管,有的水管占满了,但是有的水管还有空间
我们求出增广路的流量–根据刚才链上问题的结论–就是这些边中容量的最小值
我们将路径上每一条边都减去这个占用的容量即可
这就构成了人们常说的残余网络
都减去容量了,我们只要用bfs求出原点到汇点的任意路径即可
如果不连通,算法就结束
这个算法好不好使,手动模拟就知道,请看图片

bfs求出一条增广路为
1
−
>
2
−
>
3
−
>
4
1->2->3->4
1−>2−>3−>4
减去流量得下图

找不出增广路了,答案为
1
1
1
但是显然答案就不是
1
1
1,选取
1
−
>
2
−
>
4
1->2->4
1−>2−>4,
1
−
>
3
−
>
4
1->3->4
1−>3−>4两条增广路,答案显然为
2
2
2,我们的算法就这样炸了
(2)走回头路–EK算法
我们发现,无论怎么选取增广路,我们很难找出一个贪心策略一次得到最优解,选取不同增广路得到的结果不同
如果我们能走回头路多好
但是减去容量是算法成立的基础,我们不能动这一步
所以,我们要引入最大流的精髓–反向边
还是那个例子,自来水厂给你家送水,已经找到一条路径
但是,你说水不够,再给我送点,然而此时水管被占用了
那咋办,你直接把水送回去呗
所以,减去的容量,我们建反向边,把水送回去,就是走回头路
回归问题,我们求出
1
−
>
2
−
>
3
−
>
4
1->2->3->4
1−>2−>3−>4的增广路中,图变成了这样
(反向边用红色标出)

这下,我们可以再次找到一条增广路
1
−
>
3
−
>
2
−
>
4
1->3->2->4
1−>3−>2−>4
得到结果
2
2
2,AC了,那么,这个算法为什么是对的
其中涉及到了边
2
−
>
3
2->3
2−>3,但是如果我们手动模拟,就会发现根本不能取这条边
我们发现
3
−
>
2
3->2
3−>2这条反向边本来就代表着走回头路
但是正常
3
−
>
4
3->4
3−>4这条边已经走过了,既然你替我走了,我就替你走,直接去走路径
2
−
>
4
2->4
2−>4,这就相当于交换了位置,结果不改变
这就是EK算法,最大流问题的基础算法
附代码(c++)(问题参考洛谷P2740)
#include<bits/stdc++.h>
using namespace std;
int a[1145][1145],dist[114514],n,m,start,endd;
queue<int>q;
bool vis[114514];
bool bfs(int s,int t){
memset(vis,false,sizeof(vis));
memset(dist,-1,sizeof(dist));
vis[s] = true;
dist[s] = s;
while(!q.empty()){
q.pop();
}
q.push(s);
while(!q.empty()){
int x = q.front();
q.pop();
for(int i = 1;i<=n;i++){
if(i!=x&&!vis[i]&&a[x][i]>0){
q.push(i);
dist[i] = x;
vis[i] = true;
if(i==t){
return true;
}
}
}
}
return false;
}
int EK(int s,int t){
int ans = 0;
while(bfs(s,t)){
int mins = 0x3f3f3f3f;
for(int i = t;i!=s;i = dist[i]){
mins = min(mins,a[dist[i]][i]);
}
for(int i = t;i!=s;i = dist[i]){
a[i][dist[i]]+=mins;
a[dist[i]][i]-=mins;
}
ans+=mins;
}
return ans;
}
int main() {
cin>>n>>m>>start>>endd;
for(int i = 1;i<=m;i++){
int u,v,w;
cin>>u>>v>>w;
a[u][v]+=w;
}
int ans = EK(start,endd);
cout<<ans;
return 0;
}
(3)EK的弊端
EK算法是正确的,但是时间复杂度非常玄学
比如说这种图

如果使用EK算法,
2
−
>
3
2->3
2−>3那条边的方向会不断切换,这样下去将会找
200
200
200次增广路
直接TLE
EK算法可以优化,每次处理出最短路径,但是这也没有解决EK慢的问题,尤其是在更加稠密的图,EK的复杂度显然不够优秀
所以,为了解决这种问题,DINIC诞生了
(4)化图为树–DINIC算法
EK一次只能找一条增广路
其实就是把图变成链
如果我们想要从源点出发一次找多条增广路呢?
我们把图变成树,怎么变?
显然,用bfs分层,形成的就是一棵树了
然而进行一次bfs不一定正确
那进行多少次bfs呢?这个就很玄学
每次的残余网络的分层都不相同,所以,可以通过一直进行bfs知道搜索不出增广路
有了搜索树,这就可以引入dfs了,一次搜更多的增广路
不仅提高了稠密图中的时间复杂度,还防止了反复更新增广路的问题
这就是DINIC,在bfs建出的搜索树上跑dfs
代码中的体现就是储存每个点的层次
DINIC还有一个著名的当前弧优化
因为搜索树上有重复点,这些重复点连的边已经更新了的话,就不会再更新,所以我们标记一个
c
u
r
cur
cur数组即可
其实,在DINIC之外还有ISAP等算法
但是在信奥中有个不成文的规定,不能卡DINIC
新手可以先掌握DINIC
附代码(c++)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int INF = 0x3f3f3f3f;
ll nxt[114514],to[114514],w[114514];
ll idx = 1,head[114514];
ll n,m,s,t;
ll dep[114514],cur[114514];
ll ans = 0;
queue<ll> q;
void addedge(ll u,ll v,ll ww){
idx++;
nxt[idx] = head[u];
to[idx] = v;
w[idx] = ww;
head[u] = idx;
}
bool bfs(){
for(int i = 1;i<=n;i++){
dep[i] = INF;
}
while(!q.empty()){
q.pop();
}
q.push(s);
dep[s] = 0;
cur[s] = head[s];
while(!q.empty()){
ll x = q.front();
q.pop();
for(ll i = head[x];i!=0;i = nxt[i]){
ll y = to[i];
if(w[i]>0&&dep[y]==INF){
q.push(y);
cur[y] = head[y];
dep[y] = dep[x]+1;
if(y==t){
return true;
}
}
}
}
return false;
}
ll dfs(ll x,ll res){
if(x==t){
return res;
}
ll sum = 0,k,i;
for(i = cur[x];i&&res;i = nxt[i]){
cur[x] = i;
ll y = to[i];
if(w[i]>0&&(dep[y]==dep[x]+1)){
k = dfs(y,min(res,w[i]));
if(!k){
dep[y] = INF;
}
w[i]-=k;
w[i^1]+=k;
sum+=k;
res-=k;
}
}
return sum;
}
void DINIC(){
while(bfs()){
ans+=dfs(s,INF);
}
}
signed main(){
cin>>n>>m>>s>>t;
for(ll i = 1;i<=m;i++){
ll u,v,ww;
cin>>u>>v>>ww;
addedge(u,v,ww);
addedge(v,u,0);
}
DINIC();
cout<<ans;
return 0;
}
4后记
本蒟蒻的第一篇博客讲的是最短路,如今20篇过去了,这是第21篇
我这个大蒟蒻终于学会了网络流
本文作者是蒟蒻,如有错误请各位神犇指点
森林古猿出品,必属精品,请认准CSDN森林古猿1