目录
1、拆解多个数的加法
2、进位保存加法器
3、CSA的优点和缺点
4、CSA电路的实现
文章总目录点这里:《基于FPGA的数字信号处理》专栏的导航与说明
1、拆解多个数的加法
考虑3个4bits数相加,10 + 4 + 7 = 21 的过程是这样的:
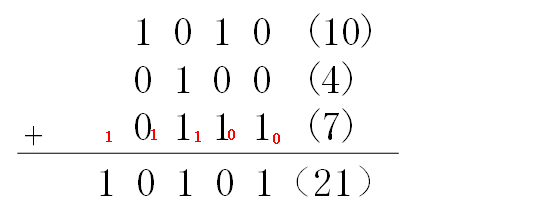
其中的红色数字是由低位向高位产生的进位,因为进位值是直接在当前位与3个加数相加,所以我们也可以把进位值拆解出来,改写成如下格式:
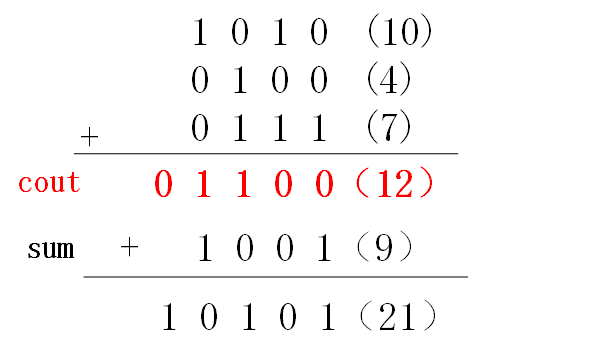
cout是低位产生的进位。例如,最低位的3个值是0/0/1,所以产生了向高位的进位0;次低位的3个值是1/0/1,所以产生了向高位的进位1。
sum是不考虑进位值时3个数相加的和。例如,最低位的3个值是0/0/1,所以该位的和为1;次低位的3个值是1/0/1,所以该位的和为0。
这样分别产生了进位cout = 01100,和sum=1001,二者相加后的结果就是最终3个数的和即21。这种方法相当于把3个数的加法转换成了2个数的加法。
2、进位保存加法器
上面这种将3个数的加法转换成两个数加法形式的电路就叫做 进位保存加法器(Carry Save Adder, CSA)。
当3个数中有2个或3个1时就会向高位产生进位,而和的值则和1的个数相关,奇数个1时和为1,偶数个1时和为0,所以它的真值表如下:
| 加数1 | 加数2 | 加数3 | 结果 | 进位 |
|---|---|---|---|---|
| a | b | c | sum | cout |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
如果你仔细点观察,就会发现上面的真值表和全加器FA的真值表是一样的,这不就说明CSA就是FA吗?只是FA的进位输入都改成了第3个加数,如下:
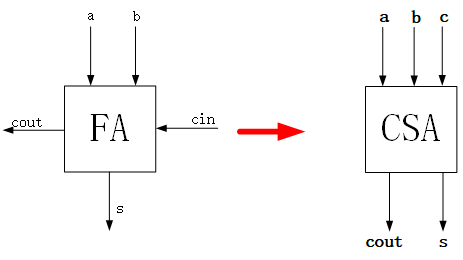
对于3个4bits的加法,就可以用4个CSA来组成:
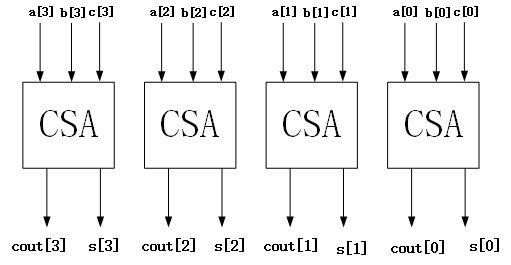
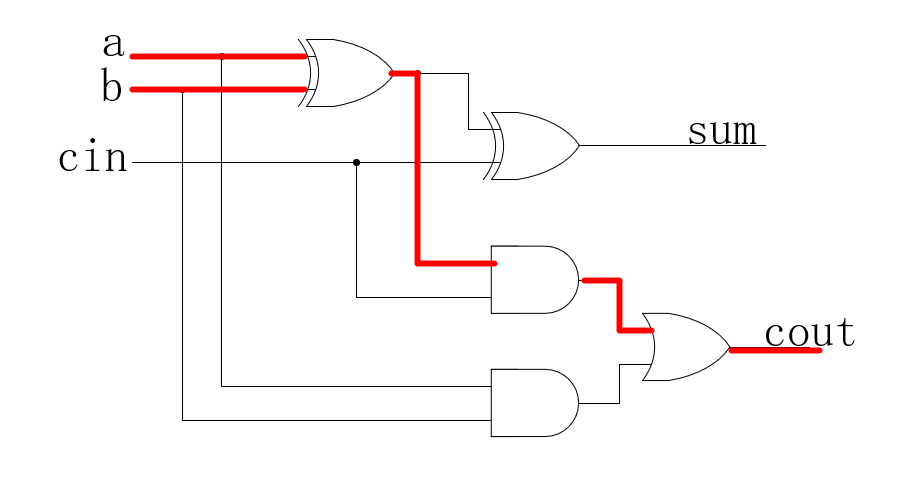
可以看到这样结构的加法器的关键路径的延迟是多少呢?一个CSA电路的延迟,也就是一个FA的延迟,如下(3个门电路):
3、CSA的优点和缺点
上面说了3个数的加法,如果使用CSA电路,那么关键路径的延迟只有3个门电路,而如果使用常规的RCA(行波进位加法器)呢?考虑6个4bits数相加,其一般的电路结构如下:
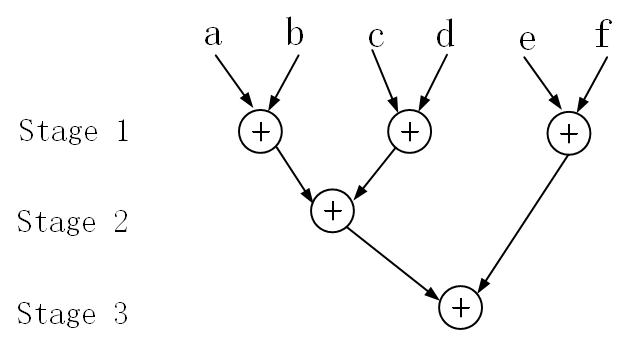
如果其中的加法器是RCA,那么该电路的关键路径延迟是3级加法器的延迟。如果采用CSA电路,则其电路结构如下:
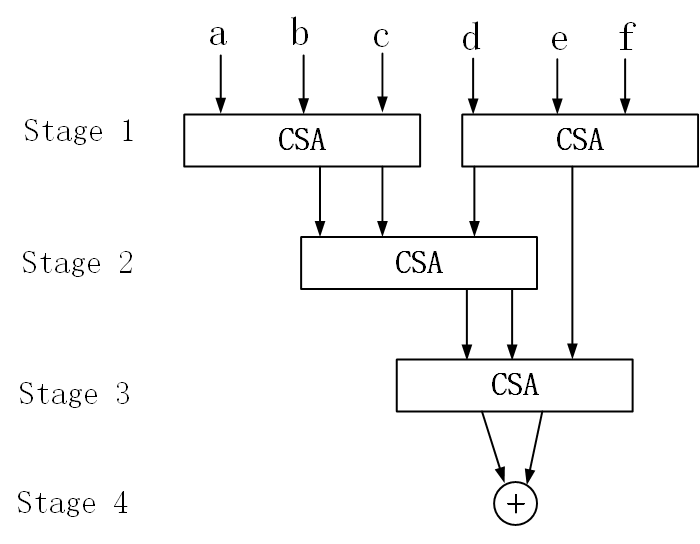
前面说了,CSA电路的延迟也就一个门电路,那么上面电路的关键路径延迟就是 3个门电路 + 最后的加法器 的延迟,假设加法器也是使用的RCA加法器,那么最终的延迟就是 1个RCA的延迟 + 3个门电路 延迟,这显然比3级RCA电路的延迟要小。可以预见的是,随着加数个数的增加,两种电路的延迟差距还会拉大。
以4比特乘法为例,其竖式计算表示如下:
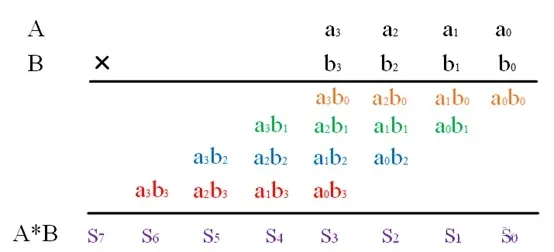
ai和bi分别表示A和B的某个bit,aibi表示ai与bi相与,使用与门电路生成,aibi的值只有0和1。S表示AB相乘的结果。每一列使用半加器HA或全加器FA两两相加,其结果表示为Si,每一列每两个数产生的进位将传递至相邻高的一列参与计算。其电路结构如下(其中虚线箭头表示进位传播的路线):
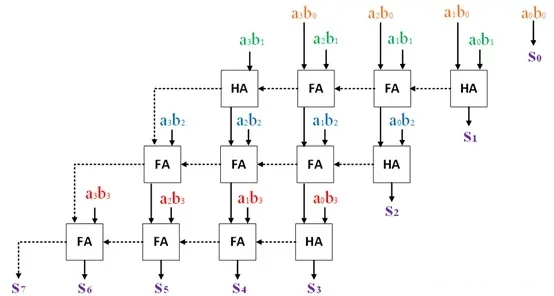
根据进位传播链,可以看出该电路的关键路径如下:
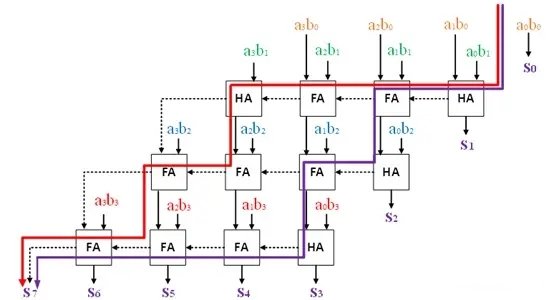
红线和紫线是由于累加造成的进位链的最长路径。其中:
-
红色路径:6个FA + 2个HA
-
紫色路径:5个FA + 3个HA
使用进位保留加法器CSA可缩短该进位链的传播延时,其电路结构如下:
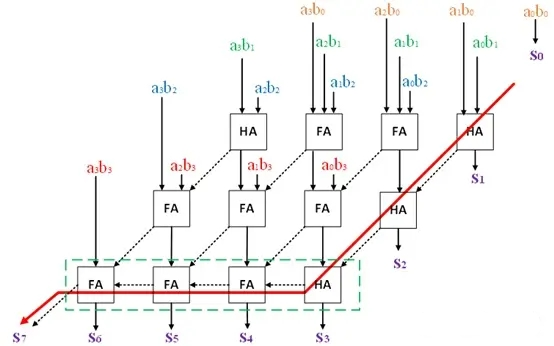
将RCA阵列乘法器的进位连接至斜下角的加法器,CSA结构的阵列乘法器将进位与和分别计算,不必计算该层的进位,省去了行波进位加法器进位链的依赖,只在最后一级通过RCA结构(上图绿色虚框)传递进位合并最后的结果。上图红色是CSA结构的关键路径:3个FA + 3个HA。可见,CSA结构使用相同的资源却有更优的时序性能,当加法个数变多时,这一优势将更大。
进位保存加法器的优点如下:
-
进位保存加法器将 3 个数字的加法减少到 2 个数字
-
由于进位传播级很少,与其他类型的加法器相比,它的功耗较低
-
该加法器可以一次执行三位加法
-
无论最终操作完成,下一级都会使用简单的 N 位 RCA。
进位保存加法器的缺点如下:
-
在进位保存加法的每一步中,可以立即知道加法结果,但我们不知道加法结果与给定数字相比是更小还是更大。
-
这种类型的加法器不能解决将 2 个整数相加以生成单个输出的问题。相反,它只是将 3 个整数相加并生成两个整数,因此两个整数的总和等于三个输入的总和。
-
它对于少数位操作具有高功耗和传播延迟。
4、CSA电路的实现
接下来,以6个8bits有符号数的加法为例,看如何用CSA的树形结构实现。首先要确定的是,对于单个bit的CSA来说,就是全加器,如下:
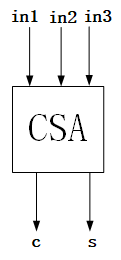
所以它的生成公式是:
s = in1 ^ in2 ^ in3; c = (in1&in2) | (in1&in3) | (in2&in2) ;
第1级有2个CSA电路,它们实现3个8bits的加法。第1个CSA的输入是3个加数a,b,c,输出是8bit的和csa11_s 跟 进位csa11_c,需要注意的是进位csa11_c在参与下级加法的时候要左移1bit(即乘2),因为它是向高位的进位。代码如下:
//第1级的第1个 CSA
assign csa11_in1 = a;
assign csa11_in2 = b;
assign csa11_in3 = c;
assign csa11_s = csa11_in1 ^ csa11_in2 ^ csa11_in3;
assign csa11_c = (csa11_in1 & csa11_in2) | (csa11_in1 & csa11_in3) | (csa11_in2 & csa11_in3);第2个CSA的输入是3个加数d,e,f,输出是8bit的和csa12_s 跟 进位csa12_c,需要注意的是进位csa12_c在参与下级加法的时候要左移1bit(即乘2),因为它是向高位的进位。代码如下:
//第1级的第2个 CSA
assign csa12_in1 = d;
assign csa12_in2 = e;
assign csa12_in3 = f;
assign csa12_s = csa12_in1 ^ csa12_in2 ^ csa12_in3;
assign csa12_c = (csa12_in1 & csa12_in2) | (csa12_in1 & csa12_in3) | (csa12_in2 & csa12_in3);第2级只有1个CSA,它的输入是第1级第1个CSA的两个输出和第2个CSA的一个输出,因为输入中有两个数是上级CSA产生的进位,所以需要左移1位,这样原本的8bits加法就变成了9bits加法。输出是9bit的和csa21_s 跟 进位csa21_c,需要注意的是进位csa21_c在参与下级加法的时候要左移1bit(即乘2),因为它是向高位的进位。代码如下:
//第2级的CSA
assign csa21_in1 = {csa11_c,1'b0}; //左移1比特
assign csa21_in2 = {csa11_s[7],csa11_s}; //为了适配csa21_in1,在高位补符号位
assign csa21_in3 = {csa12_s[7],csa12_s}; //为了适配csa21_in1,在高位补符号位
assign csa21_s = csa21_in1 ^ csa21_in2 ^ csa21_in3;
assign csa21_c = (csa21_in1 & csa21_in2) | (csa21_in1 & csa21_in3) | (csa21_in2 & csa21_in3);第3级只有1个CSA,它的输入是第2级的CSA的两个输出和第1级的第2个CSA的一个输出,因为输入中有1个数是上级CSA产生的进位,所以需要左移1位,这样原本的9bits加法就变成了10bits加法。输出是10bit的和csa31_s 跟 进位csa31_c,需要注意的是进位csa31_c在参与下级加法的时候要左移1bit(即乘2),因为它是向高位的进位。代码如下:
//第3级的CSA
assign csa31_in1 = {csa21_c,1'b0}; //左移1比特
assign csa31_in2 = {csa21_s[8],csa21_s}; //为了适配csa31_in1,在高位补符号位
assign csa31_in3 = {csa12_c[7],csa12_c,1'b0}; //左移1bit,在高位补符号位
assign csa31_s = csa31_in1 ^ csa31_in2 ^ csa31_in3;
assign csa31_c = (csa31_in1 & csa31_in2) | (csa31_in1 & csa31_in3) | (csa31_in2 & csa31_in3);经过3级CSA产生的 和csa31_s 跟 进位csa31_c就是6个数相加的结果,但是它不是一个直接表示的数值,而是拆成了两部分的冗余结果,所以我们还需要设计一个加法,来将这两个数相加,这样得到的结果最是最终的6个数的加法结果。这里仍然要注意,进位需要左移1bit(乘2),如下:
//第4级加法-------------------------------------------------------------------------------------
//把 和 + 进位,得到最终的加法结果。因为进位要左移1位,所以和也要在高位补符号位
assign sum = {csa31_c,1'b0} + {csa31_s[9],csa31_s};综上,总体的RTL代码如下:
//CSA的生成公式:
// s = in1 ^ in2 ^ in3;
// c = (in1&in2) | (in1&in3) | (in2&in3) ;
module csa(
input [7 :0] a,b,c,d,e,f,
output [10:0] sum_1
);
//----------------------------------------------------------
//定义有关wire
wire [7:0] csa11_in1,csa11_in2,csa11_in3;
wire [7:0] csa12_in1,csa12_in2,csa12_in3;
wire [7:0] csa11_s,csa11_c;
wire [7:0] csa12_s,csa12_c;
//第1级的第1个 CSA
assign csa11_in1 = a;
assign csa11_in2 = b;
assign csa11_in3 = c;
assign csa11_s = csa11_in1 ^ csa11_in2 ^ csa11_in3;
assign csa11_c = (csa11_in1 & csa11_in2) | (csa11_in1 & csa11_in3) | (csa11_in2 & csa11_in3);
//第1级的第2个 CSA
assign csa12_in1 = d;
assign csa12_in2 = e;
assign csa12_in3 = f;
assign csa12_s = csa12_in1 ^ csa12_in2 ^ csa12_in3;
assign csa12_c = (csa12_in1 & csa12_in2) | (csa12_in1 & csa12_in3) | (csa12_in2 & csa12_in3);
//第2级-------------------------------------------------------------------------------------
//定义有关wire,因为上级的进位是往高位进位,所以需要左移1比特,即cout是9bits,
//为了适配,其他输入也要在高位补符号位到9bits
wire [8:0] csa21_in1,csa21_in2,csa21_in3;
wire [8:0] csa21_s,csa21_c;
//第2级的CSA
assign csa21_in1 = {csa11_c,1'b0}; //左移1比特
assign csa21_in2 = {csa11_s[7],csa11_s}; //为了适配csa21_in1,在高位补符号位
assign csa21_in3 = {csa12_s[7],csa12_s}; //为了适配csa21_in1,在高位补符号位
assign csa21_s = csa21_in1 ^ csa21_in2 ^ csa21_in3;
assign csa21_c = (csa21_in1 & csa21_in2) | (csa21_in1 & csa21_in3) | (csa21_in2 & csa21_in3);
//第3级-------------------------------------------------------------------------------------
//定义有关wire,因为上级的进位是往高位进位,所以需要左移1比特,即cout是10bits,
//为了适配,其他输入也要在高位补符号位到10bits
wire [9:0] csa31_in1,csa31_in2,csa31_in3;
wire [9:0] csa31_s,csa31_c;
//第3级的CSA
assign csa31_in1 = {csa21_c,1'b0}; //左移1比特
assign csa31_in2 = {csa21_s[8],csa21_s}; //为了适配csa31_in1,在高位补符号位
assign csa31_in3 = {csa12_c[7],csa12_c,1'b0}; //左移1bit,在高位补符号位
assign csa31_s = csa31_in1 ^ csa31_in2 ^ csa31_in3;
assign csa31_c = (csa31_in1 & csa31_in2) | (csa31_in1 & csa31_in3) | (csa31_in2 & csa31_in3);
//第4级加法-------------------------------------------------------------------------------------
//把 和 + 进位,得到最终的加法结果。因为进位要左移1位,所以和也要在高位补符号位
assign sum_1 = {csa31_c,1'b0} + {csa31_s[9],csa31_s};
endmodule接下来写个TB测试一下电路,因为可能的输入太多了,一共有(2^8)^6 = 2^48 = 281,474,976,710,656种情况,显然不可能遍历完,所以我们采用随机测试的方式。通过生成数组随机向量来对电路进行测试:
module tb_test();
reg signed [7 :0] a,b,c,d,e,f;
wire [10:0] sum;
wire sum_flag; //结果比对正确时拉高
wire signed [10:0] sum_real;
assign sum_real = a + b + c + d + e + f; //预期的正确结果
assign sum_flag = sum == sum_real; //判断电路输出是否与预期输出一致
initial begin
//赋初值
a = 0;
b = 0;
c = 0;
d = 0;
e = 0;
f = 0;
#5;
repeat(1024)begin //设定向量个数
//生成随机向量
a = $random();
b = $random();
c = $random();
d = $random();
e = $random();
f = $random();
#5;
end
#10 $stop(); //结束仿真
end
//例化被测试模块
csa u_csa(
.a (a ),
.b (b ),
.c (c ),
.d (d ),
.e (e ),
.f (f ),
.sum (sum )
);
endmodule加法运算的预期结果也是很容易就可以找出来的,就是在TB中直接写加法就行。接着构建了向量sum_flag作为电路输出与预期结果的对比值,当二者一致时即拉高这两个信号。这样我们只要观察这个信号,即可知道电路输出是否正确。仿真结果如下:
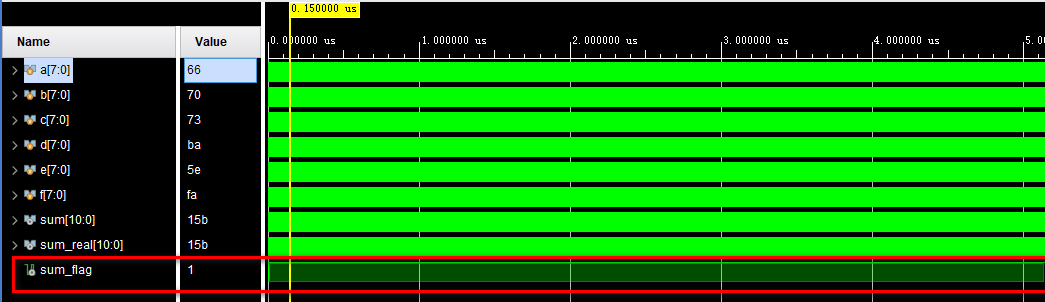
可以看到,sum_flag都是一直拉高的,说明电路输出正确。