什么是 LFU 缓存?
最少使用频率 (LFU) 是一种用于管理计算机内存的缓存算法。在这种算法中,系统会跟踪缓存中每个数据被引用的次数。当缓存已满时,系统会删除引用频率最低的数据。
LFU 缓存问题描述
我们的目标是设计一个LFU 缓存,需要支持以下操作:
- LFUCache(int capacity): 初始化具有特定容量的缓存对象。
- int get(int key): 如果键存在于缓存中,则返回该键的值;否则,返回 -1。
- void put(int key, int value): 如果键存在,则更新其值;如果键不存在,则插入该键。当缓存达到容量时,应在插入新项目之前使最少使用频率的键失效并删除它。如果存在多个频率相同的键(平局情况),则应使最近最少使用的键失效。
当对缓存中某个键执行 get 或 put 操作时,该键的频率将增加。get 和 put 操作的时间复杂度应为 O(1)。
LFU 缓存实现
使用暴力方法实现 LFU 缓存
我们初始化一个大小等于缓存大小的数组。每个元素存储键、值、频率以及该键被访问的时间戳。我们使用频率和时间戳来确定最少使用的元素。
class Element {
int key;
int val;
int frequency;
int timeStamp;
public Element(int k, int v, int time) {
key = k;
val = v;
frequency = 1;
timeStamp = time;
}
}
int get(int key): 我们遍历数组,并将缓存中每个元素的键与给定键进行比较。如果找到相等的键,则增加该元素的频率并更新时间戳。如果未找到,则返回 -1。时间复杂度为 O(n)。
void put(int key, int value): 如果数组未满,我们创建一个频率为 1 且时间戳为 0 的新元素,并增加数组中现有数据的时间戳。如果数组已满,我们必须删除最少使用的元素。为此,我们遍历数组并找到频率最低的元素。如果频率相同,则选择最近最少使用的元素(最旧的时间戳)。然后插入新元素。时间复杂度为 O(n)。
使用更高效的方法实现 LFU 缓存
首先,我们将实现 O(1) 时间复杂度的插入和访问操作。为此,我们需要两个映射,一个存储键值对,另一个存储访问次数/频率。

public class LFUCache {
private Map<Integer, Integer> valueMap = new HashMap<>();
private Map<Integer, Integer> frequencyMap = new HashMap<>();
private final int size;
public LFUCache(int capacity) {
size = capacity;
}
public int get(int key) {
if (!valueMap.containsKey(key)) {
return -1;
}
frequencyMap.put(key, frequencyMap.get(key) + 1);
return valueMap.get(key);
}
public void put(int key, int value) {
if (!valueMap.containsKey(key)) {
valueMap.put(key, value);
frequencyMap.put(key, 1);
} else {
valueMap.put(key, value);
frequencyMap.put(key, frequencyMap.get(key) + 1);
}
}
}
使用单链表实现 LFU 缓存
在上述代码中,我们需要实现缓存淘汰策略。当映射大小达到最大容量时,我们需要找到具有最低访问频率的数据。
在当前实现中,我们必须遍历 frequencyMap 的所有值,找到最低频率并从两个映射中删除相应的键。这需要 O(n) 时间。
此外,如果多个键具有相同的频率,在当前实现中我们无法找到最近最少使用的键,因为 HashMap 不存储插入顺序。为了解决这个问题,我们添加了一个新的数据结构,即一个有序映射,其中键是频率,值是具有相同频率的元素列表。
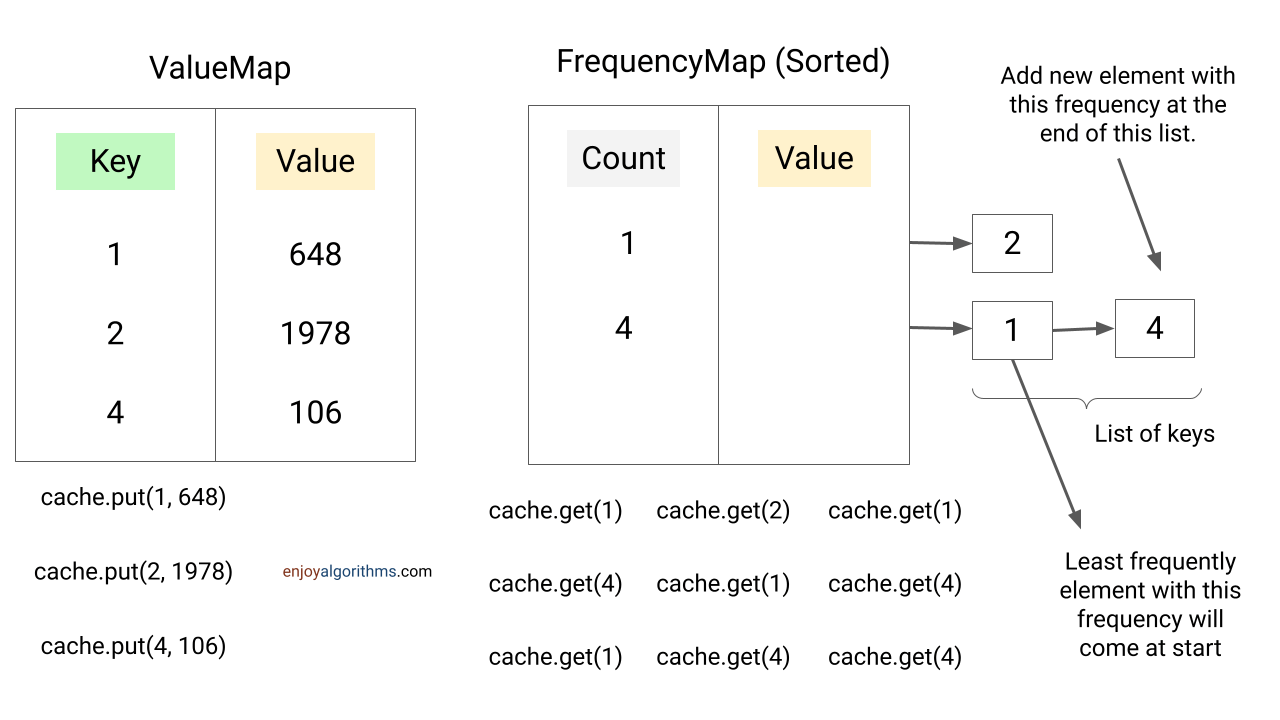
现在,新的数据可以添加到频率为 1 的链表末尾。由于映射按频率排序,我们可以在 O(1) 时间内找到最低频率的列表。此外,我们可以在 O(1) 时间内删除列表的第一个项目(最低频率的项目),因为它是最近最少使用的。
代码如下:
public class LFUCache {
private Map<Integer, Integer> valueMap = new HashMap<>();
private Map<Integer, Integer> countMap = new HashMap<>();
private TreeMap<Integer, List<Integer>> frequencyMap = new TreeMap<>();
private final int size;
public LFUCache(int capacity) {
size = capacity;
}
public int get(int key) {
if (!valueMap.containsKey(key) || size == 0) {
return -1;
}
int frequency = countMap.get(key);
frequencyMap.get(frequency).remove(new Integer(key));
if (frequencyMap.get(frequency).size() == 0) {
frequencyMap.remove(frequency);
}
frequencyMap.computeIfAbsent(frequency + 1, k -> new LinkedList<>()).add(key);
countMap.put(key, frequency + 1);
return valueMap.get(key);
}
public void put(int key, int value) {
if (!valueMap.containsKey(key) && size > 0) {
if (valueMap.size() == size) {
int lowestCount = frequencyMap.firstKey();
int keyToDelete = frequencyMap.get(lowestCount).remove(0);
if (frequencyMap.get(lowestCount).size() == 0) {
frequencyMap.remove(lowestCount);
}
valueMap.remove(keyToDelete);
countMap.remove(keyToDelete);
}
valueMap.put(key, value);
countMap.put(key, 1);
frequencyMap.computeIfAbsent(1, k -> new LinkedList<>()).add(key);
} else if (size > 0) {
valueMap.put(key, value);
int frequency = countMap.get(key);
frequencyMap.get(frequency).remove(new Integer(key));
if (frequencyMap.get(frequency).size() == 0) {
frequencyMap.remove(frequency);
}
frequencyMap.computeIfAbsent(frequency + 1, k -> new LinkedList<>()).add(key);
countMap.put(key, frequency + 1);
}
}
}
因此,插入和删除操作都是 O(1),即常量时间操作。
使用双链表实现 LFU 缓存 (Java)
在解决缓存淘汰问题时,我们将访问操作的时间复杂度增加到了 O(n)。所有具有相同频率的数据元素都在一个链表中。如果其中一个元素被访问,我们需要将其移动到下一个频率的链表中。我们必须先遍历链表找到该元,这在最坏情况下需要 O(n) 操作。
为了解决这个问题,我们需要以某种方式直接在链表中访问该数据,如果我们能做到这一点,就可以在 O(1) 时间内从当前频率链表中删除该元素,并在 O(1) 时间内将其移动到下一个频率链表的末尾。
为此,我们需要一个双链表。我们将创建一个节点,存储元素的键、值和在链表中的位置。我们将把链表转换为双链表。

public class LFUCache {
private Map<Integer, Node> valueMap = new HashMap<>();
private Map<Integer, Integer> countMap = new HashMap<>();
private TreeMap<Integer, DoubleLinkedList> frequencyMap = new TreeMap<>();
private final int size;
public LFUCache(int n) {
size = n;
}
public int get(int key) {
if (!valueMap.containsKey(key) || size == 0) {
return -1;
}
Node nodeToDelete = valueMap.get(key);
Node node = new Node(key, nodeToDelete.value());
int frequency = countMap.get(key);
frequencyMap.get(frequency).remove(nodeToDelete);
removeIfListEmpty(frequency);
valueMap.remove(key);
countMap.remove(key);
valueMap.put(key, node);
countMap.put(key, frequency + 1);
frequencyMap.computeIfAbsent(frequency + 1, k -> new DoubleLinkedList()).add(node);
return valueMap.get(key).value;
}
public void put(int key, int value) {
if (!valueMap.containsKey(key) && size > 0) {
Node node = new Node(key, value);
if (valueMap.size() == size) {
int lowestCount = frequencyMap.firstKey();
Node nodeToDelete = frequencyMap.get(lowestCount).head();
frequencyMap.get(lowestCount).remove(nodeToDelete);
removeIfListEmpty(lowestCount);
int keyToDelete = nodeToDelete.key();
valueMap.remove(keyToDelete);
countMap.remove(keyToDelete);
}
frequencyMap.computeIfAbsent(1, k -> new DoubleLinkedList()).add(node);
valueMap.put(key, node);
countMap.put(key, 1);
} else if (size > 0) {
Node node = valueMap.get(key);
Node nodeToInsert = new Node(key, value);
int frequency = countMap.get(key);
frequencyMap.get(frequency).remove(node);
removeIfListEmpty(frequency);
valueMap.remove(key);
countMap.remove(key);
valueMap.put(key, nodeToInsert);
countMap.put(key, frequency + 1);
frequencyMap.computeIfAbsent(frequency + 1, k -> new DoubleLinkedList()).add(nodeToInsert);
}
}
private void removeIfListEmpty(int frequency) {
if (frequencyMap.get(frequency).size() == 0) {
frequencyMap.remove(frequency);
}
}
}
class Node {
private final int key;
private final int value;
private Node previous;
private Node next;
public Node(int k, int v) {
key = k;
value = v;
}
public int key() {
return key;
}
public int value() {
return value;
}
}
class DoubleLinkedList {
private Node head = new Node(0, 0);
private Node tail = new Node(0, 0);
private int size = 0;
public DoubleLinkedList() {
head.next = tail;
tail.previous = head;
}
public void add(Node node) {
node.previous = tail.previous;
node.previous.next = node;
node.next = tail;
tail.previous = node;
size++;
}
public void remove(Node node) {
node.previous.next = node.next;
node.next.previous = node.previous;
size--;
}
public Node head() {
return head.next;
}
public int size() {
return size;
}
}
双链表确保我们可以在常数时间内删除节点和插入节点。总的来说,插入和访问操作都是 O(1) 时间复杂度。
LRU缓存的实际应用
假设我们有一个代理服务器,它位于用户和互联网之间。当用户请求网页内容时,这个代理服务器会在用户和互联网之间进行中转,同时缓存一些内容,比如图片、CSS 文件、JavaScript 代码等。以优化网络利用率和提高响应速度。
这样的缓存代理应该在其有限的存储或内存中,尽量缓存尽可能多的数据。但是代理服务器的存储空间有限,所以它需要决定哪些内容应该保留在缓存中,哪些内容应该删除。
这里就有一个问题:到底应该删除哪些内容?最好的策略是删除那些不常用的内容,而保留那些经常被访问的内容。
LFU(Least Frequently Used,最少使用频率) 缓存算法正是用来解决这个问题的。LFU 会跟踪每个内容被访问的次数,当缓存满了需要删除一些内容时,它会选择删除那些访问次数最少的内容。这样,可以确保那些最有用、最常被访问的内容能够保留在缓存中,提高系统的效率。
**相比之下,如果使用 LRU(Least Recently Used,最近最少使用) 缓存算法,**它会删除那些最近没有被访问过的内容。这在很多情况下也有效,但如果用户的请求模式是轮流访问多个内容,LRU 可能会不断地删除和添加内容,导致缓存命中率降低。
例如,如果用户依次访问 A、B、C、D 四个资源,而代理服务器的缓存只能存三个资源。LRU 会不断地删除最久没访问的资源,导致缓存一直在变化,无法有效利用缓存。而 LFU 会保留访问次数最多的资源,不会频繁地删除和添加,可以更好地提高缓存命中率。
总之,在需要频繁处理大量请求的场景中,比如网络代理服务器,使用 LFU 缓存算法可以更有效地利用缓存,提高系统的整体性能。