最近这一两周看到不少互联网公司都已经开始秋招提前批了。不同以往的是,当前职场环境已不再是那个双向奔赴时代了。求职者在变多,HC 在变少,岗位要求还更高了。
最近,我们又陆续整理了很多大厂的面试题,帮助一些球友解惑答疑,分享技术面试中的那些弯弯绕绕。
《AIGC 面试宝典》圈粉无数!
《大模型面试宝典》(2024版) 发布!
喜欢本文记得收藏、关注、点赞。更多实战和面试交流,欢迎交流
Hyperparameter
超参数(Hyperparameter),是机器学习算法中的调优参数,用于控制模型的学习过程和结构。与模型参数(Model Parameter)不同,模型参数是在训练过程中通过数据学习得到的,而超参数是在训练之前由开发者或实践者直接设定的,并且在训练过程中保持不变。
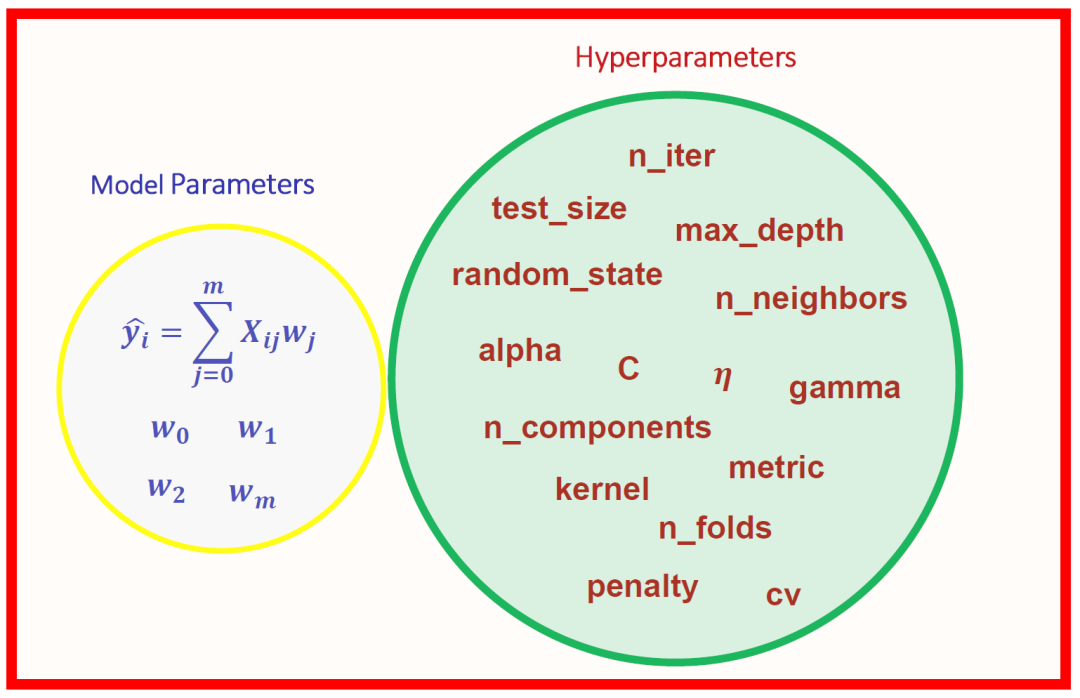
Hyperparameter vs Model Parameter
超参数是机器学习算法在开始执行前需要设置的一些参数,这些参数的值会影响算法的表现,但不会通过训练过程自动调整。
-
需要人工设置:超参数的值不是通过训练过程自动学习得到的,而是需要训练者根据经验或实验来设定。
-
影响模型性能:超参数的选择会直接影响模型的训练过程和最终性能。
-
需要优化:为了获得更好的模型性能,通常需要对超参数进行优化,选择最优的超参数组合。
需要自己设定,不是机器自己找出来的,称为超参数(hyperparameter)。

Hyperparameter
超参数大致可以分为三类:神经网络结构的超参数、神经网络训练过程的超参数和神经网络中过拟合的超参数。
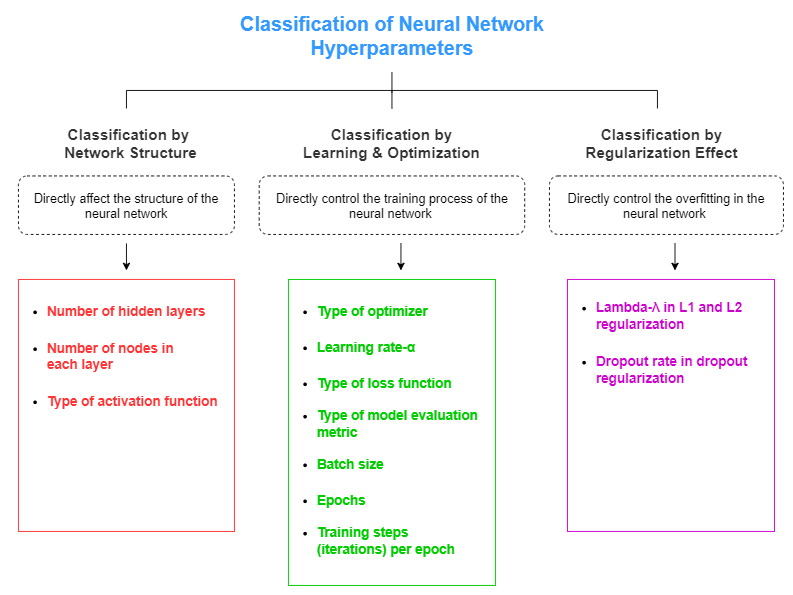
Hyperparameter
一、神经网络结构的超参数
直接影响神经网络结构的超参数主要包括网络层数(Layers)和每层的神经元数量(Neurons per Layer),它们共同决定了神经网络的深度和宽度,进而影响其学习复杂特征的能力、训练难度、计算资源需求以及可能存在的过拟合风险。此外,虽然激活函数(Activation Function)不直接改变网络结构,但它通过引入非线性变换,显著影响网络的表达能力和性能,是神经网络设计中不可忽视的关键因素。
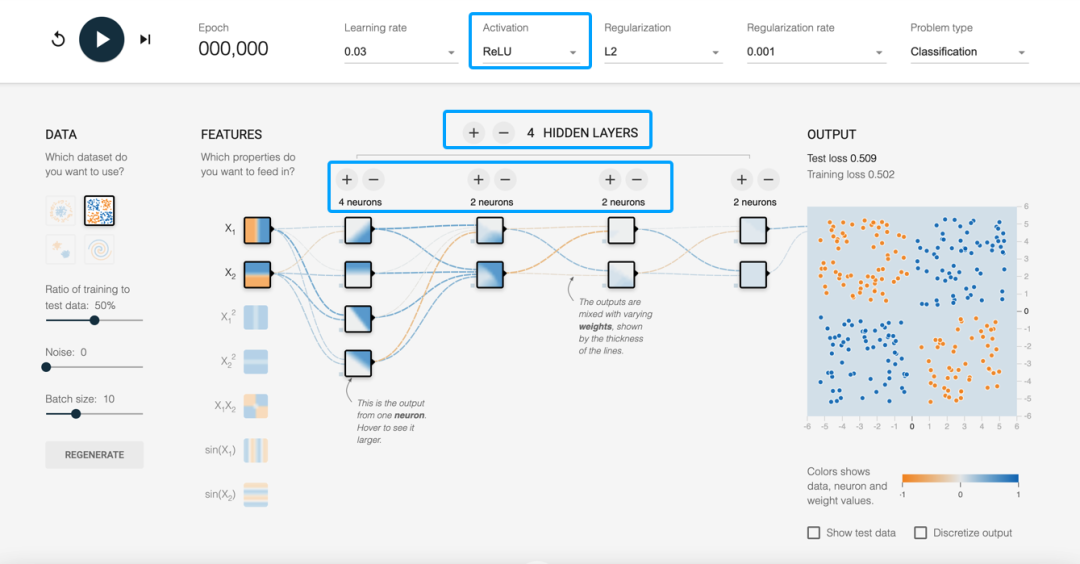
Directly affect the structure of the neural network
- 网络层数和神经元数量
-
层数(Layers):神经网络中的层数是一个关键的超参数,它决定了网络的深度。层数越多,网络能够学习到的特征就越复杂,但同时也可能导致过拟合和训练难度的增加。
-
每层的神经元数量(Neurons per Layer):每一层中的神经元数量也是一个重要的超参数。神经元数量越多,网络的学习能力就越强,但同时也需要更多的计算资源和训练时间。
-
调整策略:根据问题的复杂度和数据集的规模来选择合适的网络层数和神经元数量。通常,更深的网络和更多的神经元可以处理更复杂的问题,但也可能导致过拟合和计算成本增加。
- 激活函数(Activation Function)
-
定义:决定神经元如何对其输入进行非线性变换。虽然激活函数本身不是直接改变网络结构的超参数,但不同的激活函数会影响网络的非线性能力和表达能力,从而间接影响网络的结构和性能。
-
常见类型:ReLU、Sigmoid、Tanh等。
-
选择策略:根据具体任务和网络架构选择合适的激活函数。例如,ReLU函数因其简单性和有效性而在许多深度学习任务中广泛使用。
二、神经网络训练过程的超参数
直接影响神经网络训练过程的超参数包括学习率(Learning Rate)、批量大小(Batch Size)、迭代次数(Epochs)和优化算法(Optimizer)。这些超参数共同决定了训练过程中模型权重的更新方式、训练速度、稳定性和最终性能。
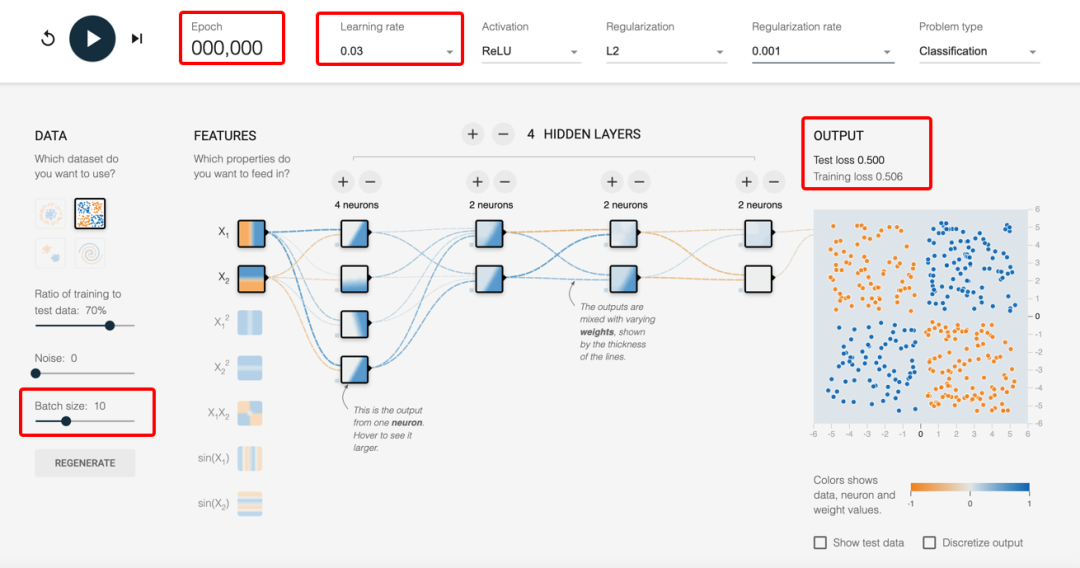
Directly control the training process of the neural network
-
定义:学习率决定了在优化过程中更新模型权重的步长。
-
影响:较高的学习率可能导致模型在训练过程中超过最优解,甚至导致训练过程发散;而较低的学习率则可能使训练过程收敛缓慢,需要更多的迭代次数。
-
调整策略:通常需要通过实验找到合适的学习率,或者采用学习率调度策略,如动态调整学习率或使用学习率衰减。
-
定义:批量大小指的是每次梯度下降迭代中使用的训练样本数量。
-
影响:较大的批量大小可以加速训练过程,因为可以并行处理更多的样本,但可能导致内存不足和泛化能力下降;较小的批量大小可以引入更多的噪声,有助于模型跳出局部最优解,但训练过程可能不稳定且收敛速度较慢。
-
选择原则:需要根据硬件资源、数据集大小和训练时间来选择合适的批量大小。
-
定义:迭代次数指的是整个训练数据集被遍历和学习的次数。
-
影响:过少的迭代次数可能导致模型未能充分学习数据集中的特征,导致欠拟合;而过多的迭代次数则可能导致模型过拟合,即模型在训练集上表现很好,但在测试集上表现不佳。
-
调整策略:通常需要通过观察验证集上的性能指标来确定合适的迭代次数。
-
定义:优化算法决定了如何更新模型参数以最小化损失函数。
-
常见优化算法:包括随机梯度下降(SGD)、动量(Momentum)、RMSprop、Adam等。
-
影响:不同的优化算法具有不同的收敛速度和性能表现。例如,Adam优化器结合了动量和RMSprop的优点,能够自动调整学习率,通常比SGD具有更快的收敛速度和更好的性能。
-
选择原则:需要根据具体问题和数据集的特点选择合适的优化算法。
三、神经网络中过拟合的超参数
正则化系数(Regularization)是直接影响神经网络中过拟合问题的关键超参数。
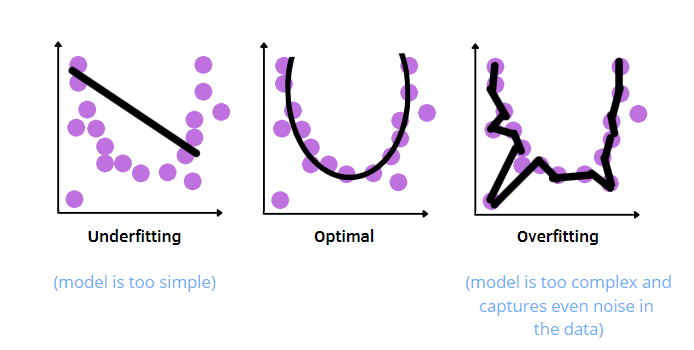
-
定义:正则化方法用于防止模型过拟合,通过在损失函数中添加正则化项来约束模型的复杂度。
-
常见正则化方法:包括L1正则化、L2正则化、Dropout等。
-
影响:正则化方法可以有效地降低模型的复杂度,提高模型的泛化能力。但是,正则化强度过大会导致模型欠拟合。
-
调整策略:需要根据验证集上的性能指标来调整正则化强度。
正则化系数是控制正则化强度的超参数。较大的正则化系数会对模型权重施加更强的约束,降低模型的复杂度,从而减少过拟合。常见的正则化方法包括L1正则化和L2正则化、Dropout等。
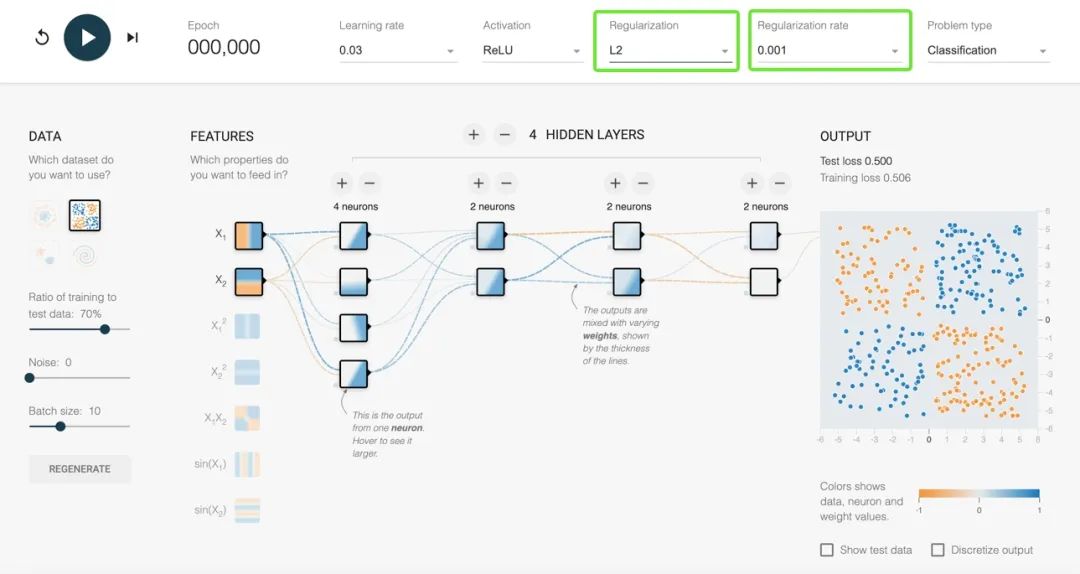
Directly control the overfitting in the neural network
-
L1正则化(Lasso Regularization):通过在损失函数中添加模型权重的绝对值之和作为惩罚项,鼓励模型产生稀疏的权重,即许多权重为零。这有助于模型的解释性,并可能减少过拟合。
-
L2正则化(Ridge Regularization):通过在损失函数中添加模型权重的平方和作为惩罚项,鼓励模型权重趋于较小的值,但不会像L1那样产生完全为零的权重。L2正则化有助于平滑模型的决策边界,减少过拟合。
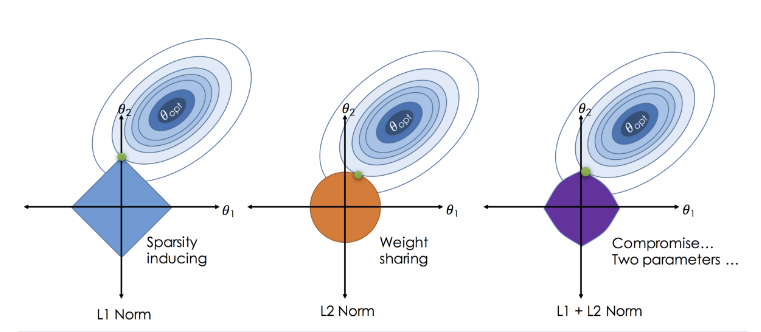
L1、L2正则化
- Dropout:虽然严格来说不是通过修改损失函数来实现的,但Dropout也是一种正则化技术。在训练过程中,它随机地将网络中一定比例的神经元输出置为零,这相当于在每次迭代时训练一个不同的网络子集。这有助于减少神经元之间的共适应性,从而提高模型的泛化能力。
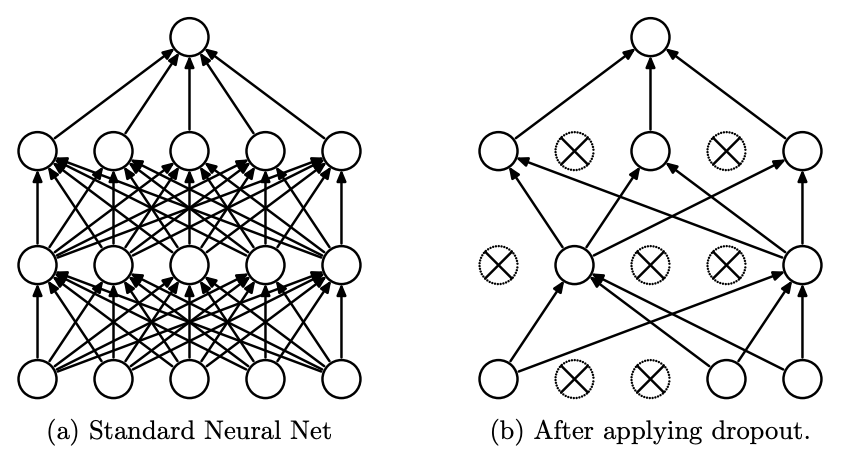
Dropout