主要讲述了通过栈来解决后缀表达式,来计算出表达式的结果,可以好好熟悉一下思路。
目录
前言
一、表达式求值问题
二、栈模拟计算表达式
1.算法思路
2.代码解释
三、代码实现
1.代码如下:
2.测试样例如下:
3.运行结果如下:
总结
前言
主要讲述了通过栈来解决后缀表达式,来计算出表达式的结果,可以好好熟悉一下思路。
一、表达式求值问题
给定一个表达式,其中运算符仅包含 +,-,*,/(加 减 乘 整除),可能包含括号,请你求出表达式的最终值。
注意:
- 数据保证给定的表达式合法。
- 题目保证符号
-只作为减号出现,不会作为负号出现,例如,-1+2,(2+2)*(-(1+1)+2)之类表达式均不会出现。 - 题目保证表达式中所有数字均为正整数。
- 题目保证表达式在中间计算过程以及结果中,均不超过 2^31 - 1。
- 题目中的整除是指向 0取整,也就是说对于大于 0 的结果向下取整,例如 5/3=1,对于小于 0 的结果向上取整,例如 5/(1−4)=−1。
- C++和Java中的整除默认是向零取整;Python中的整除
//默认向下取整,因此Python的eval()函数中的整除也是向下取整,在本题中不能直接使用。
输入格式
共一行,为给定表达式。
输出格式
共一行,为表达式的结果。
数据范围
表达式的长度不超过 100000。
二、栈模拟计算表达式
1.算法思路

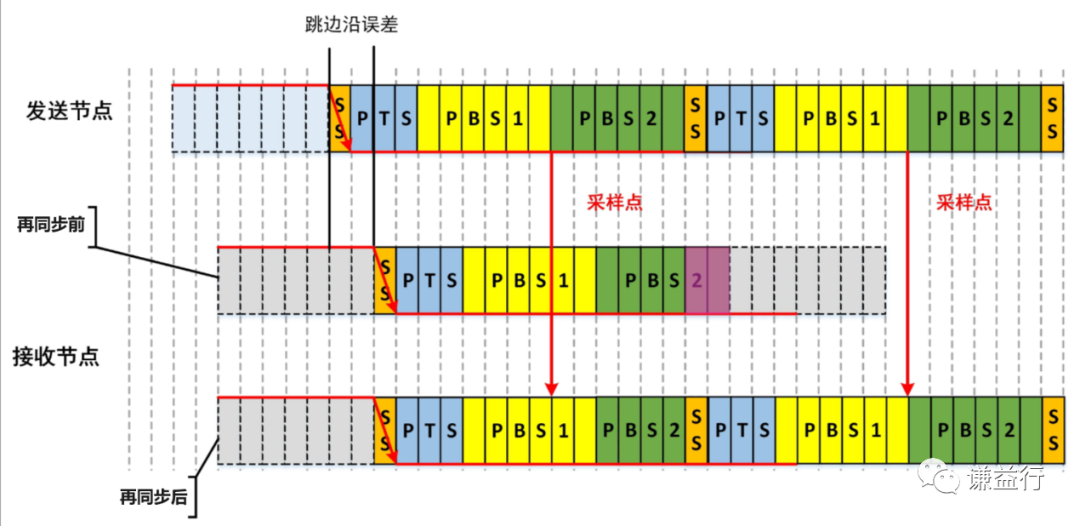
图1.1示例
当我们要计算一个表达式的结果的时候,我们平常所看到的式子其实就是中缀表达式,即图1.1中树的中序遍历(左根右)的结果,当然其中缺少了小括号。然而计算机识别的时候后缀表达式往往更容易计算,即树的后序遍历(左右根)。
那么我们如何让计算机来实现对后缀表达式进行计算呢?
模拟栈计算中缀表达式的步骤可以分为几个关键阶段,主要是通过栈来处理运算符和操作数,以正确求解表达式的值。
1.操作数栈和运算符栈的准备:
- 准备两个栈:一个用于存放操作数(数字)的栈 ,一个用于存放运算符和括号的栈 。
2.遍历表达式:
- 从左到右逐个读取表达式中的字符或子串。
3.处理操作数:
- 遇到操作数(通常是连续的数字),将其压入操作数栈。
4.处理运算符:
遇到运算符或括号时,根据其优先级和结合性进行处理:
- 左括号
(:直接将其压入运算符栈。 - 右括号
):从运算符栈中弹出运算符,并依次执行相应的计算,直到遇到匹配的左括号为止。 - 其他运算符:比较当前运算符与栈顶运算符的优先级:
- 如果当前运算符优先级高于栈顶运算符,将当前运算符压入运算符栈 。
- 否则,从运算符栈中弹出栈顶运算符,并执行相应的计算操作,直到当前运算符可以入栈为止。

根据上图这个式子,我们可以很明白的看出,当我们此时的操作符 *,那么我们符号栈中对应的操作符就是+,*号的优先级大于+,那么我们正常的顺序是先算乘除后算加减,那么就验证了,当我们当前运算符的优先级大于符号栈顶优先级的时候是不进行运算的,此时将对应的操作数和符号分别压入符号栈和操作数栈中即可。
(且符号栈中符号的运算级一定是递增的)
如果我们此时当前的运算符是/,此时栈顶操作符是*,乘除是属于同一个优先级的,所以我们此时就可以将操作数栈中弹出两个数进行运算,将运算后的结果加入操作数栈,此时再将*弹出,此时的运算符是*,栈顶是+,那么我们也是先算乘法再算加法。此时就说明了,当前运算符的优先级大于等于栈顶运算符的优先级时,就可以进行运算符栈弹出一个元素,

2.代码解释
首先创建两个栈,一个是操作数栈num,一个是运算符号栈op;用一个map集合用来表示运算符的优先级
接下来我们读入表达式str。遍历每一个字符,当字符是数字的时候,我们还需要判断它的下一位还是不是数字,如果还是数组说明是一个整数,那么就将数组压入操作数栈。如果不是数字,就说明此时是运算符。如果此时是操作符,我们就要判断此时操作符是否是括号,左括号直接压入运算符号栈;如果是右括号,那么我们当运算符栈弹出的运算符不是左括号的时候,依次进行弹出一个运算符,两个操作数,进行相应运算,并将运算结果压入操作数栈。(此时运算符栈中优先级一定是递增的)。当此时符号栈中是空的,我们直接把当前运算符直接压入运算符号栈即可;当此时运算符不是上述任意一种情况时,当运算符号栈不为空,且当前符号栈不是左括号且当前运算符的优先级大于运算符号栈的栈顶元素的优先级时,我们还是进行依次进行弹出一个运算符,两个操作数,进行相应运算,并将运算结果压入操作数栈。此时再将当前运算符压入运算符栈顶即可。
当我们整个表达式遍历结束时,如果运算符号栈仍有元素的时候,就说明还没运算结束,且运算符号栈优先级一定是递增的,我们依次进行弹出一个运算符,两个操作数,进行相应运算,并将运算结果压入操作数栈。最后操作数栈最后剩下的一个元素就行表达式的最后结果。

三、代码实现
1.代码如下:
import java.io.*;
import java.util.*;
public class 表达式求值 {
static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer st = new StreamTokenizer(br);
static Stack<Integer> num = new Stack<>();
static Stack<Character> op = new Stack<>();
public static void main(String[] args)throws Exception {
Map<Character, Integer> map = new HashMap<>();
map.put('+', 1);
map.put('-', 1);
map.put('*', 2);
map.put('/', 2);
String str = nextLine();
int len = str.length();
for(int i=0; i<len; i++) {
char ch = str.charAt(i);
if(Character.isDigit(ch)) {
int x = 0, j = i;
while (j < len && Character.isDigit(str.charAt(j))) {
x = x * 10 + str.charAt(j) - '0';
j++;
}
num.push(x);
i = j - 1;
}else if(str.charAt(i)=='(') {
op.push(str.charAt(i));
}else if(str.charAt(i)==')') {
while(op.peek() != '(') {
eval();
}
op.pop();
} else if (op.isEmpty()) {
op.push(str.charAt(i));
} else {
while(!op.isEmpty() && op.peek() != '(' && map.get(op.peek()) >= map.get(str.charAt(i))) {
eval();
}
op.push(str.charAt(i));
}
}
while(op.size() > 0) {
eval();
}
pw.println(num.peek());
pw.flush();
}
public static void eval(){
int num1 = num.pop();
int num2 = num.pop();
char x = op.pop();
if(x =='+'){
num.push(num2 + num1);
}else if(x =='-'){
num.push(num2 - num1);
}else if(x =='*'){
num.push(num2 * num1);
}else if(x =='/'){
num.push(num2 / num1);
}
}
public static int nextInt()throws Exception{
st.nextToken();
return (int)st.nval;
}
public static String nextLine()throws Exception{
return br.readLine();
}
}
2.测试样例如下:
(2+2)*(1+1)3.运行结果如下:
84 * 2 = 8
总结
上述主要讲述了通过栈来解决后缀表达式,来计算出表达式的结果,可以好好熟悉一下思路。