学懂C语言（三十三）：C语言递归详解

news2025/1/29 14:12:42

一、C语言递归

1、语法格式

2、流程图

示例1：数的阶乘

示例2：斐波那契数列

二、递归的基本要素

三、递归的工作原理

四、递归的优势与劣势

五、递归的应用示例

六、递归与非递归（迭代）的比较

一、C语言递归

递归指的是在函数的定义中使用函数自身的方法。

1、语法格式

void recursion()
{
   statements;
   ... ... ...
   recursion(); /* 函数调用自身 */
   ... ... ...
}
 
int main()
{
   recursion();
}

2、流程图

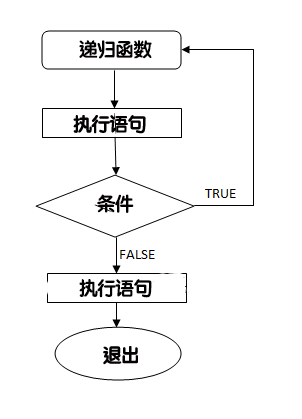
C 语言支持递归，即一个函数可以调用其自身。但在使用递归时，程序员需要注意定义一个从函数退出的条件，否则会进入死循环。

递归函数在解决许多数学问题上起了至关重要的作用，比如计算一个数的阶乘、生成斐波那契数列，等等。

示例1：数的阶乘

下面的实例使用递归函数计算一个给定的数的阶乘：

#include <stdio.h>
 
double factorial(unsigned int i)
{
   if(i <= 1)
   {
      return 1;
   }
   return i * factorial(i - 1);
}
int  main()
{
    int i = 15;
    printf("%d 的阶乘为 %f\n", i, factorial(i));
    return 0;
}

示例2：斐波那契数列

下面的实例使用递归函数生成一个给定的数的斐波那契数列：

#include <stdio.h>
 
int fibonaci(int i)
{
   if(i == 0)
   {
      return 0;
   }
   if(i == 1)
   {
      return 1;
   }
   return fibonaci(i-1) + fibonaci(i-2);
}
 
int  main()
{
    int i;
    for (i = 0; i < 10; i++)
    {
       printf("%d\t\n", fibonaci(i));
    }
    return 0;
}

二、递归的基本要素

基准情形（Base Case）：这是递归的终止条件，即一个或多个不再进行递归调用的情况。基准情形是递归能够停止并返回结果的“出口”。
递归步骤（Recursive Step）：在递归函数中，除了基准情形外，必须包含至少一个调用函数自身的步骤。这个调用将问题分解成更小的子问题。

三、递归的工作原理

栈的使用：在C语言中，递归的实现依赖于调用栈（Call Stack）。每次函数调用时，都会将当前函数的局部变量、参数、返回地址等信息压入栈中。当函数返回时，这些信息会从栈中弹出，用于恢复调用前的状态。递归调用会不断地压栈，直到达到基准情形并开始解栈。
深度限制：由于栈的大小是有限的，因此递归的深度也受到限制。如果递归调用过深，可能会耗尽栈空间，导致栈溢出错误。

四、递归的优势与劣势

优势：
- 简洁性：递归代码通常比迭代（循环）代码更简洁，更易于理解，特别是对于解决树形结构或分治策略问题。
- 自然性：对于某些问题，递归提供了一种更自然的解决方案，因为它直接反映了问题的结构。
劣势：
- 空间复杂度：递归调用会占用额外的栈空间，可能导致栈溢出。
- 性能问题：递归调用存在函数调用的开销，可能影响程序的性能。
- 调试难度：递归错误可能较难跟踪和调试，因为问题可能隐藏在多层的函数调用中。