PDF文档公众号回复关键字:20240801

2019 CSP-J 基础题3
单项选择题(共15题,每题2分,共计30分:每题有且仅有一个正确选项)
11 新学期开学了,小胖想减肥,健身教练给小胖制定了两个训练方案。
方案一:每次连续跑3公里可以消耗300千卡(耗时半小时);
方案二:每次连续跑5公里可以消耗600千卡(耗时1小时)。
小胖每周周一到周四能抽出半小时跑步,周五到周日能抽出一小时跑步。
另外,教练建议小胖每周最多跑21公里,否则会损伤膝盖。
请问如果小胖想严格执行教练的训练方案,并且不想损伤膝盖,每周最多通过跑步消耗多少千卡?( )
A 3000
B 2500
C 2400
D 2520
12.—副纸牌除掉大小王有52张牌,四种花色,每种花色13张。假设从这52张牌中随机抽取13张纸牌,则至少( )张牌的花色一致
A 4
B 2
C 3
D 5
13 —些数字可以颠倒过来看,例如0、1、8颠倒过来还是本身,6颠倒过来是9, 9颠倒过来看还是6,其他数字颠倒过来都不构成数字。
类似的,一些多位数也可以颠倒过来看,比如106颠倒过来是901。
假设某个城市的车牌只由5位数字组成,每一位都可以取0到9。
请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌?
A 60
B 125
C 75
D 100
14 假设一棵二叉树的后序遍历序列为DGJHEBIFCA,中序遍历序列为DBGEHJACIF,则其前序遍历序列为( )
A ABCDEFGHIJ
B ABDEGHJCFI
C ABDEGJHCFI
D ABDEGHJFIC
15 以下哪个奖项是计算机科学领域的最高奖?( )
A 图灵奖
B 鲁班奖
C 诺贝尔奖
D 普利策奖
2 相关知识点
1) 抽屉原理
抽屉原理也被称为鸽巢原理,它是组合数学中一个重要的原理,由德国数学家狄利克雷于1834年提出的。
把这3苹果放到2个抽屉里,无论怎样放,总有一个抽屉至少放 2个苹果

分析
总共有如下几种放法:
0个苹果都放入箱子A,3个苹果放入箱子B
0个苹果都放入箱子A,3个苹果放入箱子B
1个苹果都放入箱子A,2个苹果放入箱子B
2个苹果都放入箱子A,1个苹果放入箱子B
关注对象是放入苹果多的箱子,一定存在的可能性,因此是总有一个抽屉(放入苹果多的箱子)至少有2个(可能有3个)
2) 乘法原理
做一件事,完成它需要分成n个步骤,做第一 步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法。
那么完成这件事共有 N=m1 * m2 * m3 …* mn 种不同的方法
每个步骤没有完成一件事,只是完成了其中一个步骤
例如
马戏团的小丑有红、黄、蓝三顶帽子和黑、白两双鞋,他每次出场演出都要戴一顶帽子、穿一双鞋。问:小丑的帽子和鞋共有几种不同搭配?
分析
演出前着装需要2步
第1步 选1顶帽子 ,有3种选法
第2步 选1双鞋子 ,有2种选法
分2步适合乘法原理,总共搭配数 3 * 2 =6 种
3) 二叉树遍历
常见的二叉树的遍历主要有3种,先序遍历,中序遍历,后序遍历
先序遍历
先序遍历又叫先根遍历,遍历的顺序为根,左孩子,右孩子
下面二叉树的前序遍历顺序为 ABDHIEJCFKG
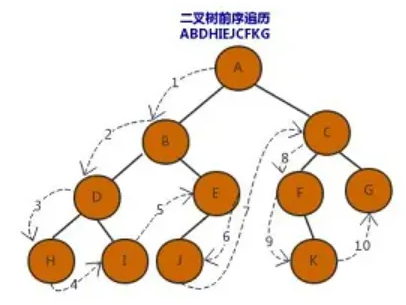
中序遍历
中序遍历又叫中根遍历,遍历的顺序为左孩子,根,右孩子
下面二叉树的中序遍历顺序为 HDIBJEAFKCG
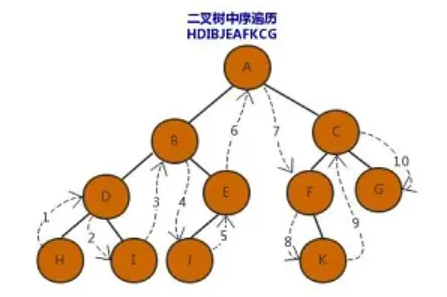
后序遍历
后序遍历又叫后根遍历,遍历的顺序为左孩子,右孩子,根
下面二叉树的后序遍历顺序为 HIDJEBKFGCA
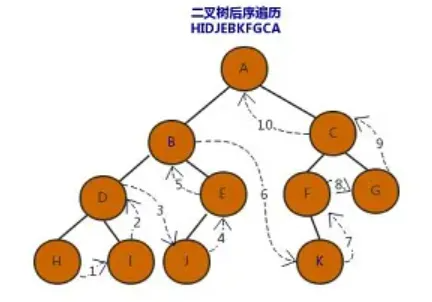
3 思路分析
11 新学期开学了,小胖想减肥,健身教练给小胖制定了两个训练方案。
方案一:每次连续跑3公里可以消耗300千卡(耗时半小时);
方案二:每次连续跑5公里可以消耗600千卡(耗时1小时)。
小胖每周周一到周四能抽出半小时跑步,周五到周日能抽出一小时跑步。
另外,教练建议小胖每周最多跑21公里,否则会损伤膝盖。
请问如果小胖想严格执行教练的训练方案,并且不想损伤膝盖,每周最多通过跑步消耗多少千卡?( C )
A 3000
B 2500
C 2400
D 2520
分析
半小时消耗300千卡,连续跑3公里
1小时消耗600千卡,连续跑5公里
想在规定公里数中,消耗更多能量,需要优先选择消耗相同能量时,跑公里少的
所以优先选1小时跑5公里,消耗600千卡
周五到周日能抽出一小时跑步,3天,消耗 3 * 600 =1800千卡,跑 3 * 5 =15 公里
还有6公里,再选周一到周四能抽出半小时跑步中的2天
2 * 300 =600 千卡
消耗能量总数=1800 + 600 =2400 千卡
12.—副纸牌除掉大小王有52张牌,四种花色,每种花色13张。假设从这52张牌中随机抽取13张纸牌,则至少( A )张牌的花色一致
A 4
B 2
C 3
D 5
分析
至少多少张牌的花色一致 -要保证一定花色一致,需要考虑最差的情况,使用最不利原则,抽屉原理
抽13张牌,总共有4个花色,考虑最不利的情况,每次都不一样,4次不一样后,再抽一张必然一样
所以13/4=3...1
至少3+1=4张花色一致
13 —些数字可以颠倒过来看,例如0、1、8颠倒过来还是本身,6颠倒过来是9, 9颠倒过来看还是6,其他数字颠倒过来都不构成数字。
类似的,一些多位数也可以颠倒过来看,比如106颠倒过来是901。
假设某个城市的车牌只由5位数字组成,每一位都可以取0到9。
请问这个城市最多有多少个车牌倒过来恰好还是原来的车牌?( C )
A 60
B 125
C 75
D 100
分析
5位数字,要使倒过来和原来一样,有如下几种情况
66099,60009,10001
第1位和第5位为0,1,8或者6或9
第2位和第4位为0,1,8或者6或9
第3位为0,1,8
第1位可以使用0,1,8,6,9这5个数字,此时第5位也固定了对应数字
第2位可以使用0,1,8,6,9这5个数字,此时第4位也固定了对应数字
第3位可以使用0,1,8这3个数字
上述可以组合的不同情况,根据乘法原理
5 * 5 *3 * 1 * 1=75
14 假设一棵二叉树的后序遍历序列为DGJHEBIFCA,中序遍历序列为DBGEHJACIF,则其前序遍历序列为( B )
A ABCDEFGHIJ
B ABDEGHJCFI
C ABDEGJHCFI
D ABDEGHJFIC
分析
根据后序遍历的特点,遍历顺序为左子树,右子树,根,可知根最后遍历,因此树或子树最后一个节点为根
根据中序遍历的特点,遍历顺序为左子树,根,右子树,可知通过根可以把子树分成左右子树
逐一拆分下去,即可获得一棵二叉树,对此二叉树前序遍历即可
A -左孩子 DBGEHJ -右孩子 CIF
DBGEHJ 根据后续遍历找根B
根据中序遍历,通过B分成左右孩子
B -左孩子 D -右孩子 GEHJ
GEHJ 根据后续遍历找根E
根据中序遍历,通过E分成左右孩子
E -左孩子 G -右孩子 HJ
HJ 通过后序遍历找根H
根据中序遍历,通过H分成左右孩子
H -右孩子J
CIF
C -左孩子 无 右孩子 IF
IF 根据后续遍历找根
根据前序遍历可知
F -左孩子 I
根据上述分析,可以构造对应二叉树
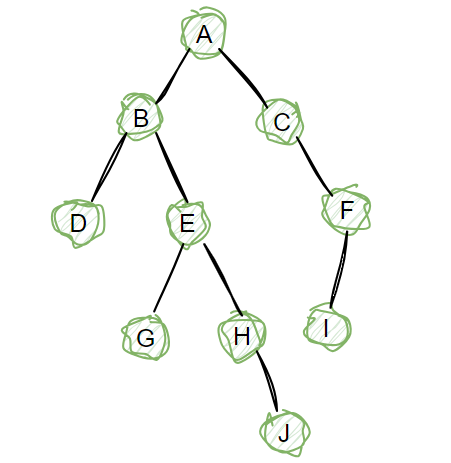
15 以下哪个奖项是计算机科学领域的最高奖?( A )
A 图灵奖
B 鲁班奖
C 诺贝尔奖
D 普利策奖
分析
图灵奖,计算机领域奖项
图灵奖是由美国计算机协会(ACM)颁发的年度奖项,旨在表彰在计算机科学领域具有持久和重大技术重要性贡献的个人。该奖项以英国数学家、逻辑学家艾伦·图灵的名字命名,他是计算机科学和人工智能的先驱,被誉为“计算机之父”
鲁班奖,建筑行业
鲁班奖是中国建筑行业工程质量最高荣誉奖,“鲁班奖”的设立,催生了一大批高质量、高水平的工程,推动了企业质量管理,提升了获奖企业的社会信誉和知名度,推动了建筑行业的“创名牌”活动
诺贝尔奖,物理、化学,医学等
诺贝尔奖是根据瑞典化学家阿尔弗雷德·诺贝尔的遗嘱于1901年设立并开始每年颁发的奖项,旨在表彰在物理学、化学、和平、生理学或医学、文学、经济学领域“对人类作出最大贡献”的科学家
普利策奖,是新闻界奖
普利策奖,正式名称为普利策新闻奖,是根据美国报业巨头约瑟夫·普利策的遗愿于1917年设立的奖项,被誉为“新闻界的诺贝尔奖”。普利策奖是美国新闻界的一项最高荣誉奖,其影响力历久不衰