SPSSAU | Power功效分析之线性回归

news2024/9/21 18:54:10

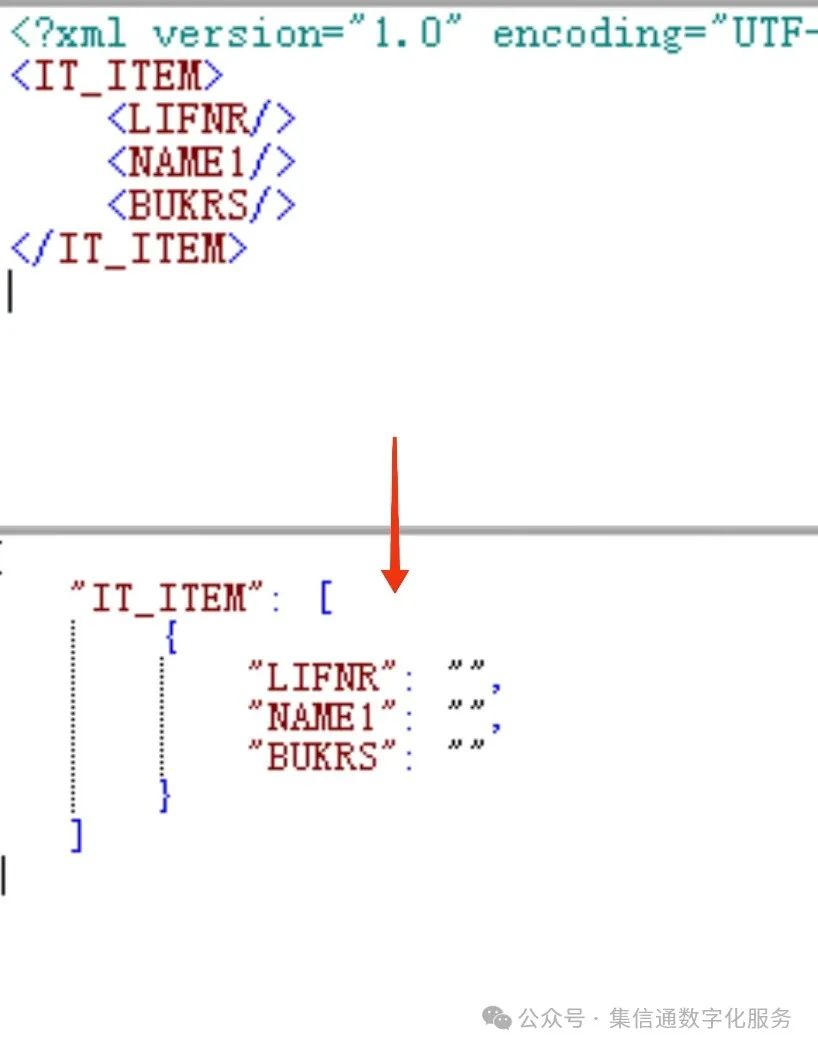
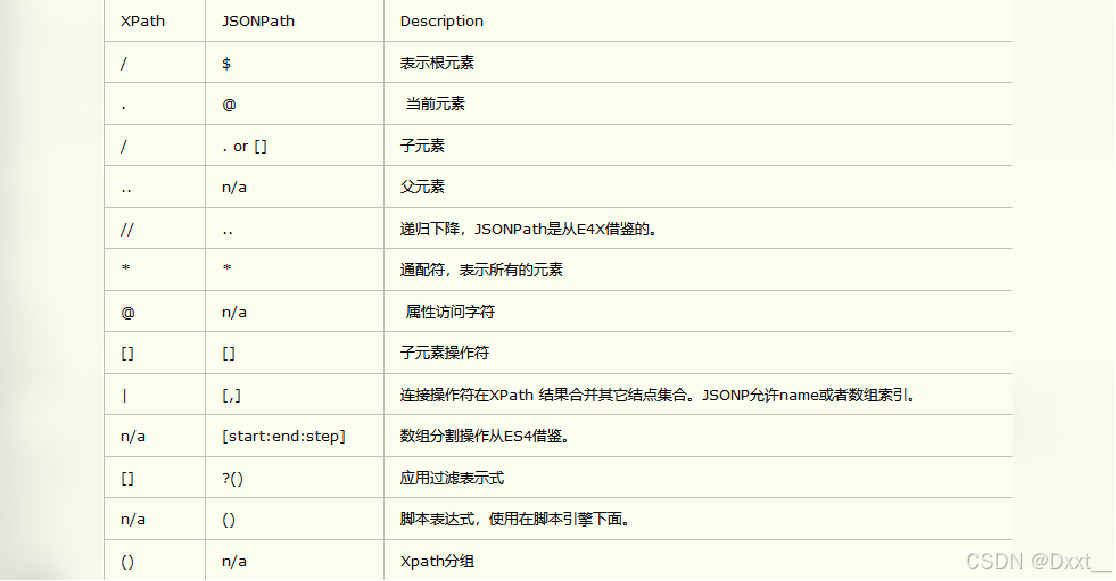
Power功效分析常用于实验研究时样本量的计算（或功效值计算），如果是涉及线性回归相关的回归系数差异计算时，SPSSAU共提供三种情况时的Power功效分析，具体如下表格所述：

名词	说明
R 方值	线性回归时R 方值或者分层回归R 方变化值的功效分析
回归系数差异	线性回归分析时回归系数差异幅度的功效分析
中介作用	中介作用效应的功效分析

比如R 方值的变化的功效能力时（也或者R 方变化值的功效能力时），此时可使用R 方值。如果是研究回归系数的差异性（包括标准化回归系数和非标准化回归系数两种情况）时，可使用‘回归系数差异’，如果研究中介作用时的功效能力情况，可使用‘中介作用’。

SPSSAU进行功效分析时，共包括两项功能，分别是计算样本量和计算功效Power值，具体涉及到Power功效原理，可查阅‘Power原理’内容。接下来以‘回归系数差异’为例具体讲解操作，如下所述：

1、关于分析Power值

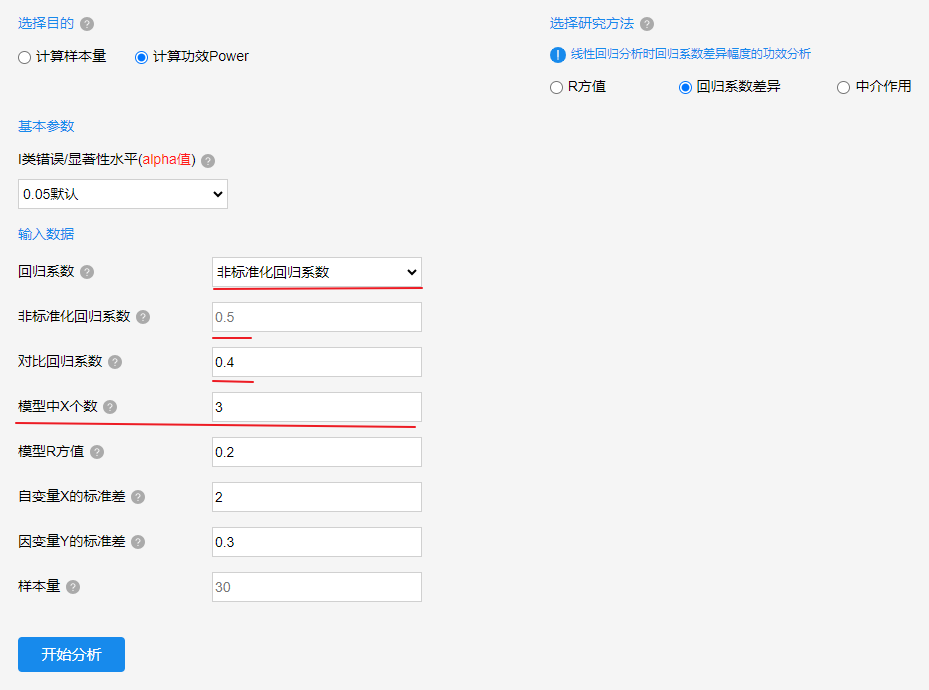
上图中目的在于计算Power值，其研究某变量的回归系数是否明显与某数字有明显差异性，上图中回归系数是‘非标准化回归系数’（当然也可提供标准化回归系数），某X和另外2个变量做线性回归模型，模型中共有3个自变量X，且R 方值是0.2，针对需要对比回归系数差异的X，其标准差值是2，并且因变量Y的标准差值是0.3；并且该X的非标准化回归系数是0.5，其需要与0.4这个数字进行对比是否有差异性。以及做线性回归模型时样本量是30个，基于当前研究，此时的Power功效水平如何呢，点击开始分析即可得到结果，最终结果如下所示：

计算结果显示，基于I类错误为0.05，线性回归样本量为30时，最终得到Power值为0.975，即不犯II类错误的概率是97.5%，即说明有97.5%的把握‘错的说成错的’。
2、关于分析样本量

上图中目的在于计算样本量，研究基于alpha值为0.05，Power为0.8，并且线性回归模型时有3个自变量X，且R 方值为0.2，以及需要研究的X它的非标准化回归系数是0.5(且其标准差值是2，因变量标准差值是0.3)，需要对比是否明显偏离0.4。最后点击开始分析即可，结果如下:

计算结果显示，基于I类错误为0.05，II类错误为0.2，Power值为0.8前提下，要想达到上述研究具有科学判断性，此时在样本量为16.623即向上取整为17时，该研究才能具有0.8的功效能力。