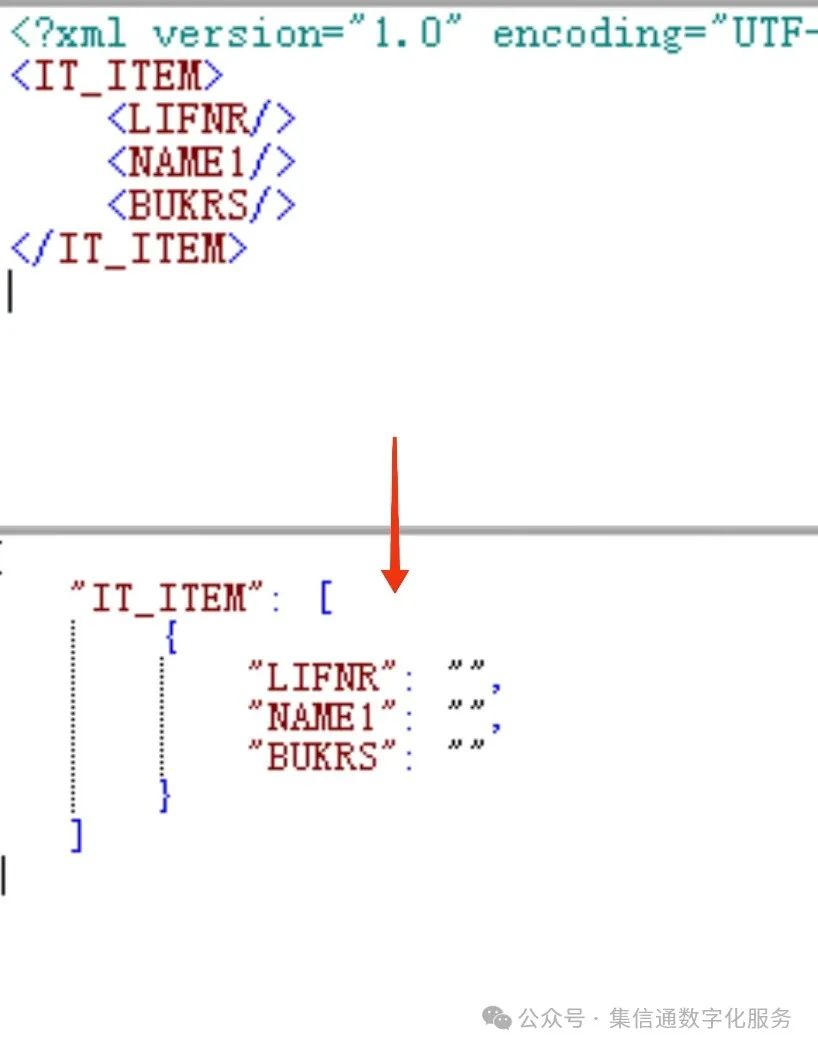
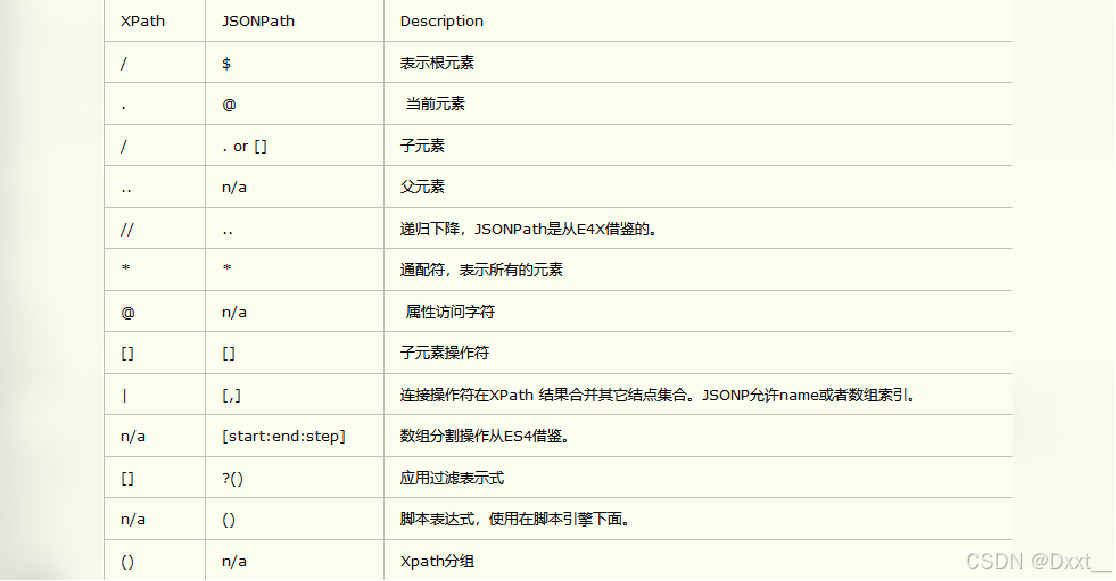
图
顶点的有穷非空集合和顶点之间边的集合
G(V,E),G:图,V:顶点集合,E:边的集合
顶点:图中的数据元素,有穷,非空
边:顶点之间的逻辑关系,边集合可以是空的
多对多:任意两个顶点之间都有可能有关系
无向边:顶点之间的边没有方向,无序偶对表示(vi,vj)
无向图:图中任意两个顶点之间的边都是无向边
无向完全图:任意两个顶点之间都存在边,n个顶点,n*(n-1)/2条边
有向边(弧):顶点之间的边有方向,有序偶对表示<vi,vj>
弧尾:vi,弧头:vj,vi->vj不可逆序
有向图:任意两个顶点之间的边都是有向边
有向完全图:任意两个顶点之间都存在方向互为相反的弧,n个顶点,n*(n-1)条边
简单图:不存在顶点到其自身的边,同一条边不重复出现
稀疏图:很少条边或弧的图
稠密图
权:图的边或弧相关的数
网:带权图
子图:假设有两个图 G=(V,{E})和 G’=(V’,{E’}),如果 V’是V真子集 且 E’是E的真子集,则称 G’为G的子图(Subgraph)
顶点和边的关系
1、 无向图:
邻接点:两点相连组成的边在图中,两点互为邻接点
边(v,v’)依附于顶点v,v’
边(v,v’)与顶点v,v’相关联
顶点的度:和顶点关联的边的数目,TD(v)
图的边数=各顶点度数之和/2
2、有向图:
<v,v’>属于图时,v邻接到v’,v’邻接自v
弧<v,v’>和顶点v,v’相关联
出度:以顶点为尾的弧的数目,OD(v)
入度:以顶点为头的弧的数目,ID(v)
顶点的度:TD(v)=ID(v)+OD(v)
图的边数=入度和=出度和
顶点v到顶点v’的路径:顶点序列,经过的每条边都是图内的边,不唯一
有向图路径也有方向
路径长度:路径上的边数或弧数
简单路径:路径中顶点不重复出现

回路(环):第一个顶点到最后一个相同顶点的路径
简单回路(环):除了第一个和最后一个顶点,其余顶点不重复

连通:顶点间有路径
连通图:任意顶点间都有路径
连通分量:连通子图,含有极大顶点数,包含依附子图顶点的所有边
强连通图:有向连通图,每个顶点间都存在路径
强连通分量:极大连通子图

连通图的生成树:
生成树:极小连通子图,含有图中全部的n个顶点,连接n个顶点的n-1条边
有向树:有向图的一个顶点入度为0(根节点),其余顶点入度为1
一个有向图的生成森林:若干棵有向树,含有图中全部顶点,只有构成树的弧

抽象数据定义
ADT 图(Graph)
Data
顶点的有穷非空集合和边的集合。
Operation
CreateGraph(*G, V,VR); // 按照顶点集V和边弧集VR的定义构造图G。
DestroyGraph(*G); // 图G存在则销毁。
LocateVex(G, u); // 若图G中存在顶点u,则返回图中的位置。
GetVex(G, v); // 返回图G中顶点v的值。
PutVex(G, v, value); // 将图G中顶点v赋值value。
FirstAdjVex(G, *v); // 返回顶点v的一个邻接顶点,若顶点在G中无邻接顶点返回空
NextAdjVex(G, v, *w); // 返回顶点v相对于顶点w的下一个邻接顶点,若w是v的最后 一个邻接点则返回“空
InsertVex(*G, v); // 在图G中增添新顶点v。
DeleteVex(*G, v); // 删除图G中顶点v及其相关的弧。
InsertArc(*G, v, w); // 在图G中增添弧<v, W>,若G是无向图,还需要增添对称弧<w, v>。
DeleteArc(*G, v, w); // 在图G中删除弧<v, w>,若G是无向图,则还删除对称弧 o
DFSTraverse(G); // 对图G中进行深度优先遍历,在遍历过程对每个顶点调用。
HFSTraverse(G); // 对图G中进行广度优先遍历,在遍历过程对每个顶点调用。
endADT
存储结构
任意2顶点都可能存在联系,物理位置不可用
度数相差很大时,多重链表不可用
邻接矩阵
一维数组存n个顶点
邻接矩阵:n*n的二维数组存边/弧
对称矩阵:n阶矩阵中a[i][j]=a[j][i]
信息:
判定两顶点之间有无边,a[i][j]==1?
顶点的度,某行1的个数
某顶点的所有邻接点,某行1的列下标
适合稠密图,读存数据多,结构修改少
array[i][j]=1;顶点i到顶点j的边存在,
array[i][j]=0;不存在

网图:边上带有权
array[i][j]=Wij;(顶点i到顶点j的边存在且权值为Wij)
array[i][j]=0;(i=j)
array[i][j]=不可能的极限值;(其他情况)

创建时间复杂度O(n+n2+e),其中矩阵初始化O(n2)
对于边数很少的图浪费空间
邻接表
一维数组存顶点,和单链表头指针
单链表,每个顶点的所有邻接点构成一个线性表,在无向图中顶点vi的边表,在有向图中vi作为弧尾的出边表
逆邻接表:以vi作为弧头的表
信息:
顶点的边表中结点的个数=顶点的度
顶点之间有无边、弧:边表中有无结点
顶点的所有邻接点
有向图的出度、入度
网图,增加weight数据域,存储权值信息

创建时间复杂度O(n+e)
十字链表
邻接表,有向图,出度入度不可共存
邻接表和逆邻接表结合
顶点表:
data数据
firstin:入边表头指针
firstout:出边表头指针
边表结构
tailvex:弧起点在顶点表的下标
headvex:弧终点在顶点表的下标
headlink:指向终点相同的下一条边
taillink:指向起点相同的下一条边

邻接多重表
邻接表,无向图删除结点复杂
ivex、jvex:某条边的两个顶点下标
ilink:依附顶点ivex的下一条边
jlink:依附顶点jvex的下一条边

边集数组
两个一维数组,存储顶点信息,存储边的信息
边数组的数据元素:起点下标begin,终点下标end,权weight
适合对边的操作

遍历
从图中某一顶点出发访问图中其余所有顶点,且每个顶点只访问一次
访问数组 visited[n],n个顶点,访问过的顶点打上标记,初值0,访问过1
深度优先类似树的前序遍历
广度优先类似树的层序遍历
深度优先搜索DFS
递归+回溯
从图中的某个顶点v出发,访问此结点,从v的未被访问的邻接点出发深度优先遍历,直到所有和v有路径相通的顶点全部被访问
非连通图,一次深度优先后,若图中有顶点未被访问,选图中一个未曾被访问的顶点做起始点
n个顶点,e条边的图
邻接矩阵是二维数组,找邻接点O(n2)
邻接表,找邻接点O(n+e)

广度优先搜索BFS
结点A入队,A所有的邻接点入队,A出队
时间复杂度相同

最小生成树
网:带权值的图
最小成本:n个顶点,n-1条边,连接成连通图,权值的和最小
最小生成树:连通网的最小代价生成树
普里姆Prim算法
假设 N=(P,{E})是连通网,TE是N上最小生成树中边的集合。
算法:
初始状态:U={u0}(u0∈V),TE={}
循环:在所有u∈U,v∈V-U的边(u,v)∈E找一条代价最小的边(u0,v0)并入集合TE,同时v0并入U,直至U=V为止。
此时 TE中必有 n-1条边,则T=(V,{TE})为N的最小生成树。
以某顶点为起点,找顶点上最小权值的边
时间复杂度 O(n2),适合稠密图


克鲁斯卡尔Kruskal算法
假设 N=(V,{E})是连通网,
初始状态:只有n个顶点而无边的非连通图 T={V,},图中每个顶点自成一个连通分量。
循环:在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。直至T中所有顶点都在同一连通分量上为止。
取图边集内权值最小的边,判断有无环
时间复杂度 O(eloge),适合稀疏图
当(i, j) 加入最小生成树时parent[i] = j
当parent[i] > 0 说明有(i, j) 存在,i=j,直到parent[i]<=0


最短路径
最短路径:两顶点之间经过的边权值之和最少的路径
源点:路径上的第一个顶点
终点:路径上的最后一个顶点
迪杰斯特拉Dijkstra算法
某一顶点到其他所有顶点
求出顶点的最短路径,基于已经求出的最短路径基础上,求的更远顶点的最短路径
时间复杂度O(n2)
任意顶点到其他所有顶点的最短路径,对每个顶点做一次Dijkstra,时间复杂度O(n3)

佛洛依德Floyd算法
所有顶点到所有顶点的最短路径

有向无环图
拓扑排序
无环有向图
AOV网:有向图+顶点表示活动,的网
顶点表示活动
弧表示活动间的优先关系
不存在回路
重点:优先关系,vi->vj:vi发生之后才可以发生vj
拓扑序列:有向图的顶点序列,序列中vi到vj有一条路径,且在顶点序列中vi在vj前面
拓扑排序:有向图构造拓扑排序的过程
网的全部顶点被输出,不存在环的AOV网
缺少顶点,存在环,不是AOV网
算法
入度为0的顶点全部入栈,栈顶输出,
删除此顶点,删除以此顶点为尾的弧(弧头元素入度-1,入度为0的入栈)
重复直到输出全部,或不存在入度为0的顶点
邻接表
n个顶点e条弧,时间复杂度O(n+e)
O(n)(扫描顶点表加入入度为0)+O(e)(出入栈,入度减一)


关键路径
AOE网:带权有向图+边表示活动,的网
顶点表示事件
有向边表示活动
边上的权值表示活动持续时间
源点:没有入边的顶点
终点:没有出边的顶点
AOE网只有一个源点,一个终点
路径长度:路径上各个活动持续的时间和
关键路径:源点到汇点具有最大长度的路径
关键活动:在关键路径上的活动
重点:减少关键路径上关键活动的时间才能减少整个工期
(顶点)最早发生时间
(顶点)最晚发生时间
(弧)最早开工时间
(弧)最玩开工时间
算法
拓扑排序,得出最早发生时间evt,拓扑序列列表stack
当k=0时:etv[k]=0;
当k≠0且< vi,vk >∈ P[k]时: etv[k]=max{etv[i]+len<vi,vk>};
根据evt和stack计算 最晚发生时间:
当k=n-1时:ltv[k]=etv[k];
当k<n-1且<vk,vj >∈ P[k]时: ltv[k]=min{etv[j]+len<vk,vj>};

活动最早发生时间=起点最早发生时间
活动最晚发生时间=终点最晚发生时间-活动时间
两者相等即为关键活动,关键路径

时间复杂度O(n+e)