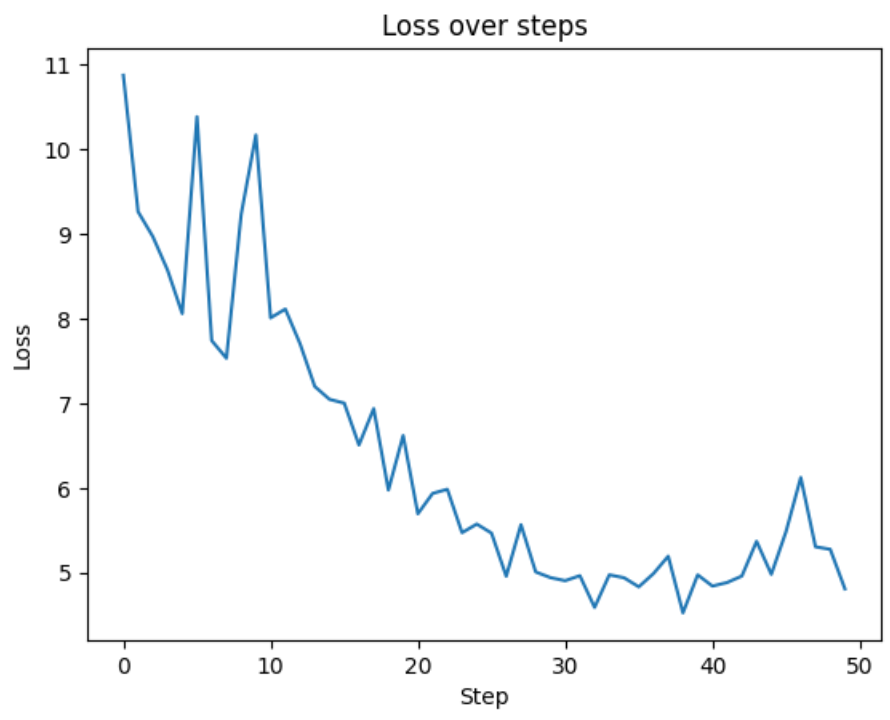
ECC(Elliptic Curve Cryptography),即椭圆曲线密码算法,是一种基于椭圆曲线数学理论的公钥加密算法。自1985年由Neal Koblitz和Victor S. Miller分别独立提出以来,ECC凭借其独特的数学原理和高效的性能,逐渐成为公认的高效和安全的加密标准。ECC算法在资源受限的设备和带宽有限的应用场景中表现出色,广泛应用于移动设备、物联网、金融交易和数字版权管理等领域。
ECC算法的基本原理
椭圆曲线
椭圆曲线是在一个平面上满足特定方程(如威尔斯特拉斯方程)的所有点的集合。在密码学中,通常使用的是一个有限域上的椭圆曲线,这意味着曲线上的点数量是有限的。椭圆曲线上的点可以进行加法和倍乘运算,这些运算遵循特定的群法则,包括封闭性、结合律、存在单位元以及每个点有一个逆元等。
密钥生成
ECC的密钥生成过程涉及多个步骤。首先,用户需要构造一条椭圆曲线E,这通常涉及到选择适当的方程和参数来定义曲线。然后,在曲线上选择一点G作为生成元,这个点通常是曲线上的一固定点,其阶(即与该点相加得到曲线上另一个点的最小正整数)为n,且n必须是一个质数。接下来,用户选择一个随机数k作为私钥,这个私钥是一个小于n的随机数。最后,通过将私钥k与生成元G相乘(在椭圆曲线的群运算下),计算出公钥Q = kG。
加密与解密
使用ECC算法进行加密时,假设要加密的明文为M,发送方选择一个随机数r,计算点R = rG和S = rP + M,其中P是接收方的公钥,而+表示椭圆曲线上的点加法。加密后的密文为(R, S)。接收方收到加密信息后,使用自己的私钥k计算点T = kR,然后计算M = S - T即可得到明文。

ECC算法的优势
密钥长度短
ECC算法的一个显著优势是密钥长度相对较短,但能提供与较长密钥的传统加密算法(如RSA)相当的安全性。例如,ECC 164位的密钥产生的安全级相当于RSA 1024位密钥提供的保密强度。较短的密钥长度意味着存储和传输成本更低,处理速度更快,特别适用于资源受限的设备如智能手机和物联网设备。
安全性高
ECC算法的安全性基于解决椭圆曲线上的离散对数问题,这是一个在计算上非常困难的问题。因此,ECC算法在保证较短密钥长度的同时,也能提供更高的安全性。攻击者需要更长的时间才能破解ECC加密的密文,这使得ECC算法成为保护敏感信息的理想选择。
加密速度快
ECC算法在加密和解密过程中的计算量相对较少,能够更快地完成加密操作。这对于需要快速处理大量数据的应用场景尤为重要,如金融交易和数字签名等。

ECC算法的应用场景
移动设备和物联网
由于移动设备和物联网设备资源有限,需要采用密钥长度短、计算量小、加密速度快的加密算法。ECC算法正是满足这些需求的理想选择,因此在移动设备和物联网领域得到广泛应用。
金融交易和数字签名
ECC算法在金融交易的安全传输和数字签名方面发挥着重要作用。通过使用ECC算法,可以确保交易的真实性和完整性,防止信息被篡改或伪造。同时,ECC算法还可以用于电子票据的签名和验证,保护电子票据的真实性和完整性。
数字版权管理
ECC算法还可以用于数字版权管理,保护知识产权,防止盗版和侵权。通过为数字内容生成唯一的数字签名,并使用ECC算法进行加密和验证,可以确保数字内容的合法性和完整性。

ECC加密算法以其独特的数学原理和高效的性能,在安全性、效率和带宽利用方面提供了显著的优势。随着计算能力的提升和安全需求的增加,ECC算法的应用范围预计将进一步扩大。尽管存在实现难度和专利限制等挑战,但ECC算法的数学之美和其在安全领域的潜力使其成为值得深入研究和投资的领域。未来,ECC算法将在更多领域发挥重要作用,为信息安全保驾护航。