
本文介绍的是另外一种针对模块控制MPC问题的一种高效求解方法。High-Performance Small-Scale Solvers for Linear Model Predictive Control,Gianluca Frison, Hans Henrik Brandenborg Sørensen, Bernd Dammann, John Bagterp Jørgensen [1]。本文讲了HPIPM的前身,HPMPC, 其实也就是HPIPM中牺牲鲁棒性的高速求解选项。核心是采用了动态规划法推导出riccati方程的形式,不过迭代速度比riccati更快。
首先有两个相似的工作,一个是CVXGEN[2]。核心思路是“. It employs a predictor-corrector Interior-Point (IP) method, and a sparse LDL factorization for the solution of the KKT system at each iteration of the IP method”,核心是采用LDL分解处理kkt矩阵。另一个方案是FORCES[3], 核心思路是:“It employs a predictor-corrector IP method, and a tailored solver for the KKT system, based on a block Cholesky factorization of the Schur complement of the KKT matrix.”处理kkt矩阵的思路稍有不同,采用了schur补kkt, 然后cholesky分解。这个思路其实在fast MPC里面也存在[4]。
这两者对比时,前面CVXGEN的问题在于:“The main disadvantages are that instruction cache is not exploited (since each instruction is executed only once), and that the code size grows with the cube of the matrices size, becoming quickly intractable.”问题维度上去就不行了。后者FROCES: “The main advantage of this approach is that the performance scales much better with the problem size. The main disadvantage is that a triple-loop based approach can attain only a small fraction of the peak performance of the processor.” 就还不错。
而本文中的原文描述是:
“The proposed algorithm for the solution of the KKT system of MPC problems is similar to the one presented in [5], with the difference that it moves the integration process one step further: the factorization and the backward recursion of the solution are fused. This allows us to reduce the number of function calls to linear-algebra routines to 3 in the factorization and 3 in the solution, for each iteration of the Riccati-like recursion.”
文章[5]也是一个反向riccati的方法。对比[5]来说,本文的核心优势就是将factorization和backward recursion结合在一起,后面可以看到,推导的结果类似riccati, 但没有显式算Riccati的P。然后这里也说了在他的Riccati-like recursion,能推出Riccati的结果,但是过程有点不一样。
线性MPC问题:
本文中想要解决的是经典的线性MPC问题:
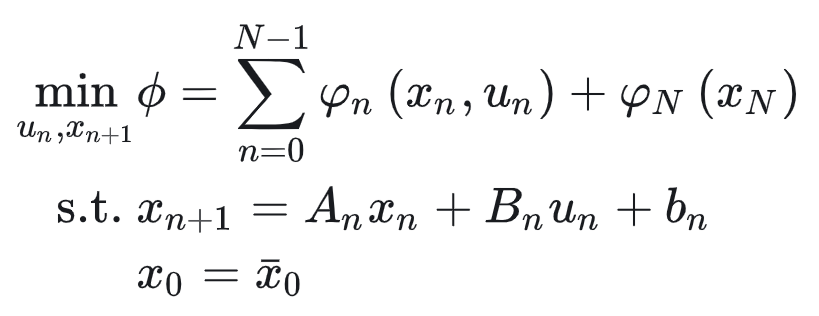
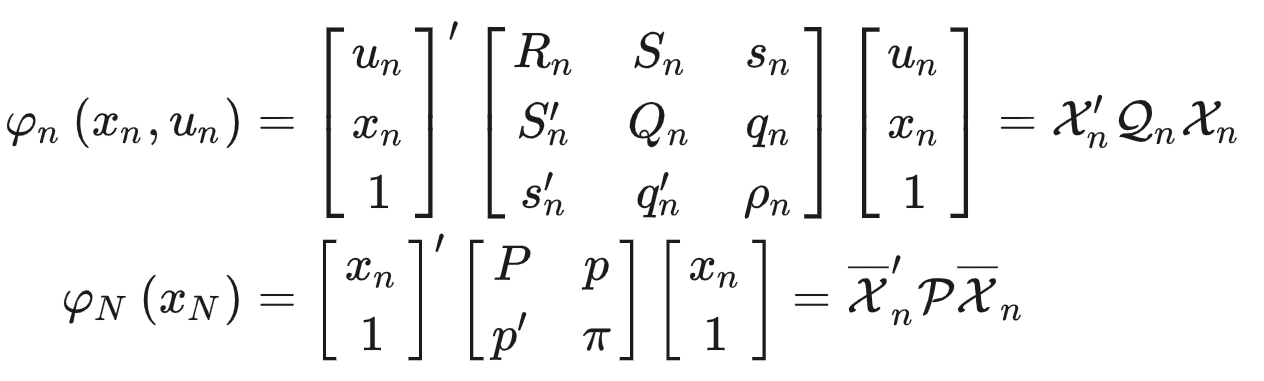
其中 n ∈ { 0 , 1 , … , N − 1 } n \in \{0,1,\dots,N-1\} n∈{0,1,…,N−1}。求解MPC问题的核心思路还是动态规划,利用动态规划的思路去做推导。
在n+1步的最优stage cost为:
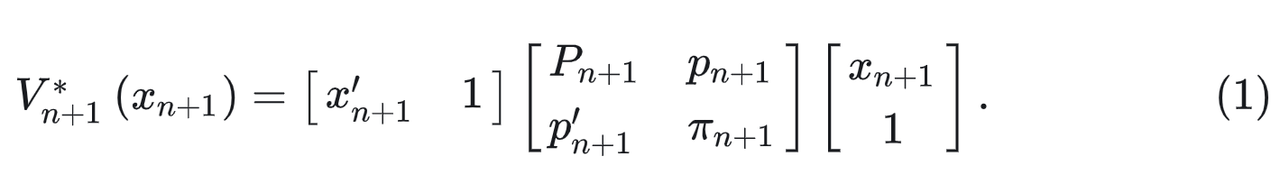
状态转移方程:
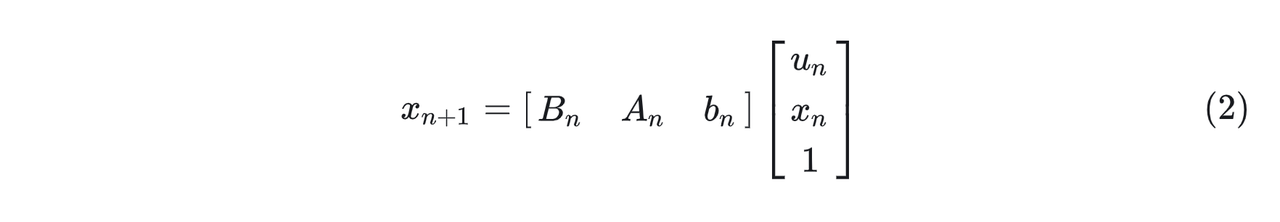
把状态转移方程(2)放进(1):
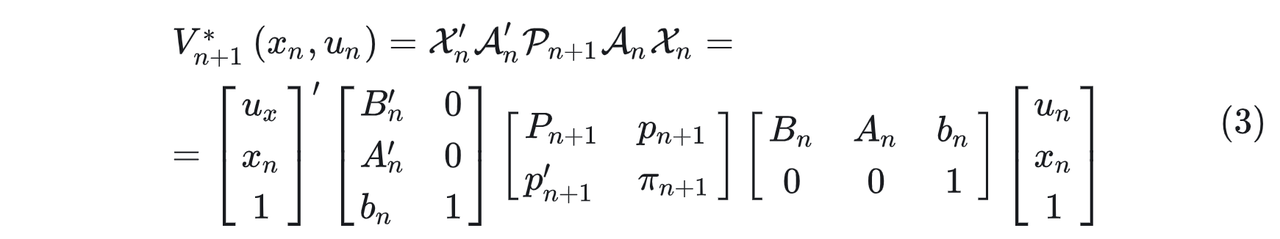
如果 P n + 1 \mathcal{P}_{n+1} Pn+1是个正定矩阵,那我们可以对其进行Cholesky分解,

最优的stage cost V n + 1 ∗ ( x n , u n ) V_{n+1}^*(x_n,u_n) Vn+1∗(xn,un)重写为:
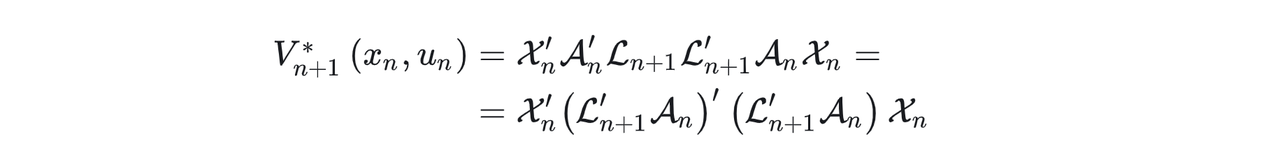
根据动态规划的思路,我们倒退回前一个stage cost
V
n
(
x
n
,
u
n
)
V_n(x_n,u_n)
Vn(xn,un),可以通过bellman公式写成:
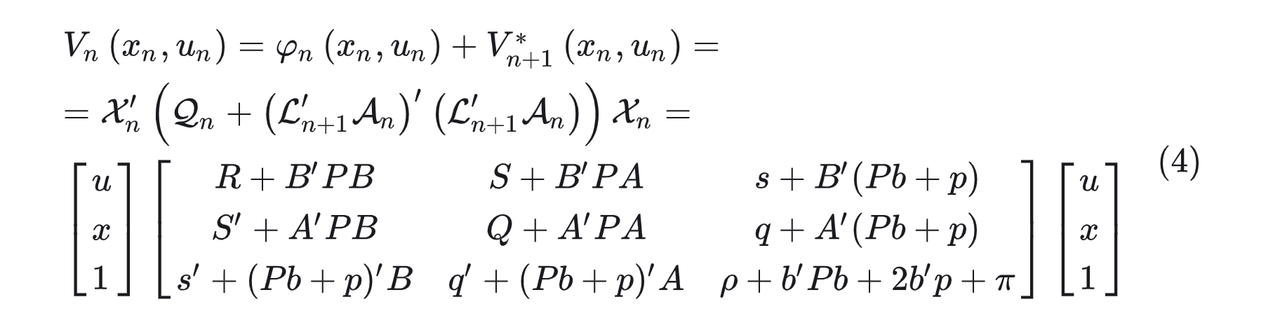
把二次型cost中间那一项单独列出来,定义成
M
n
\mathcal{M}_n
Mn,再来做一次Cholesky分解:
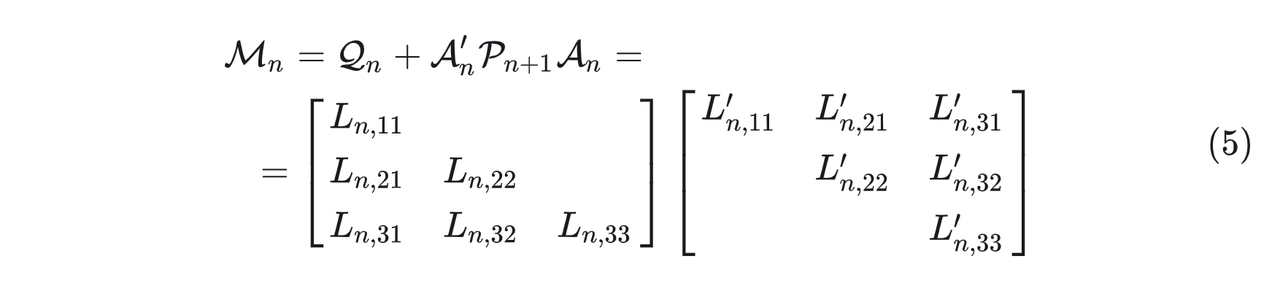
有了(5)之后,stage cost V n ( x n , u n ) V_n(x_n,u_n) Vn(xn,un)可以重新表达成如下公式:
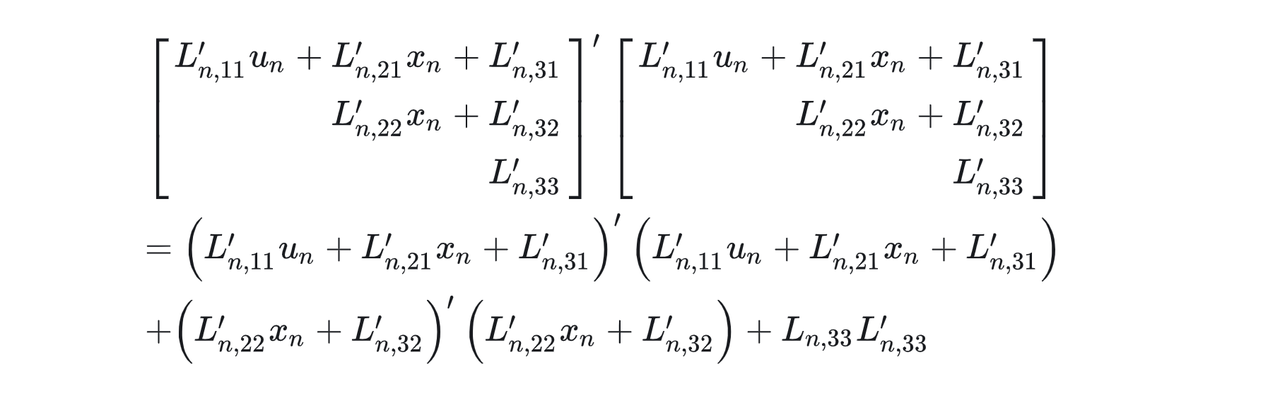
假设 x n x_n xn已知,那么对于上述stage cost V n ( x n , u n ) V_n(x_n,u_n) Vn(xn,un)求导可以得到最优控制表达:
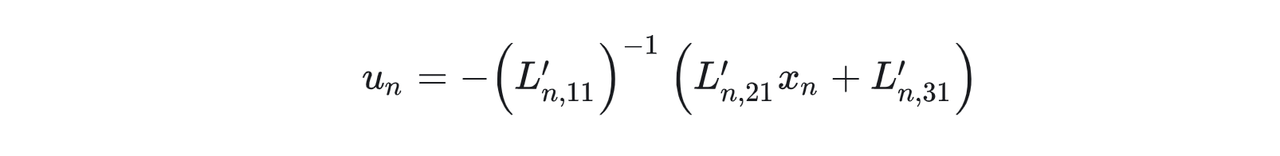
带回 V n ( x n , u n ) V_n(x_n,u_n) Vn(xn,un)可以得到基于状态 x n x_n xn的最优value function V n ∗ ( x n ) V_n^*(x_n) Vn∗(xn):

接下来还要继续根据动态规划的思路迭代stage cost V n − 1 ( x n − 1 , u n − 1 ) V_{n-1}(x_{n-1},u_{n-1}) Vn−1(xn−1,un−1)直到 t = 0 t=0 t=0,同时可以看到在 t = N − 1 t=N-1 t=N−1这里的 V n ∗ ( x n ) V_n^*(x_n) Vn∗(xn)在下一次迭代 V n − 1 ( x n − 1 , u n − 1 ) V_{n-1}(x_{n-1},u_{n-1}) Vn−1(xn−1,un−1)中就可以直接使用了,非常方便,整个算法流程伪代码为:

注意到riccati就是:
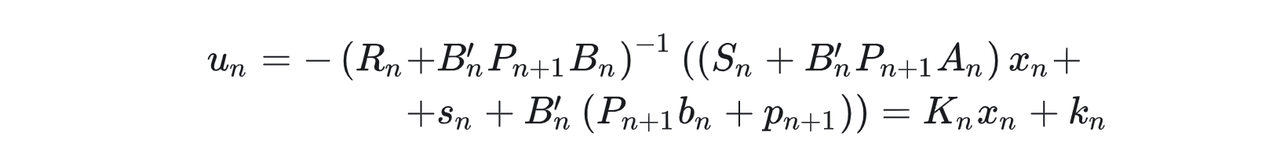
看得出和上面的u控制量的表达就是一回事。但是这里的做法我们没有显式算P,因为不需要,原文说了:“However, the procedure to compute u n u_n unas in (4) is more efficient from a computational point of view. Also notice that the recursion matrix Pn of the Riccati recursion is never computed explicitly in the above solution procedure.”这个(4)就是
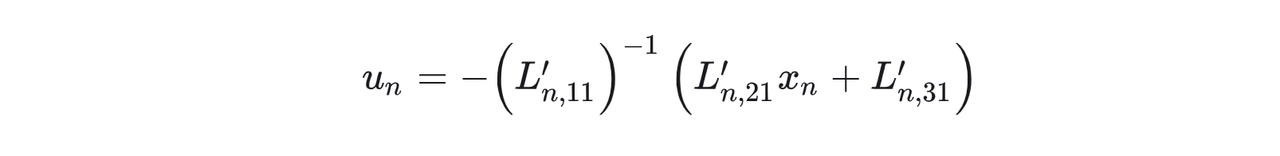
总结来说,对于每一个内点法循环,通过合理的前向迭代,本文将一次KKT矩阵分解和计算拆解成对于MPC问题中单个horizon问题的矩阵分解和计算(从 T T T时刻一直倒退计算得到 u N − 1 , … , u 0 u_{N-1}, \dots, u_0 uN−1,…,u0)。
一般线性MPC问题的求解
可以看到,如果只有系统的线性等式约束,那么只需要解一次线性方程组就可得到最优解了,解释同经典的线性约束下的QP问题,当我们引入等式约束的对偶变量 λ \lambda λ,则根据QP问题的一阶最优条件,等价于求解如下线性系统:
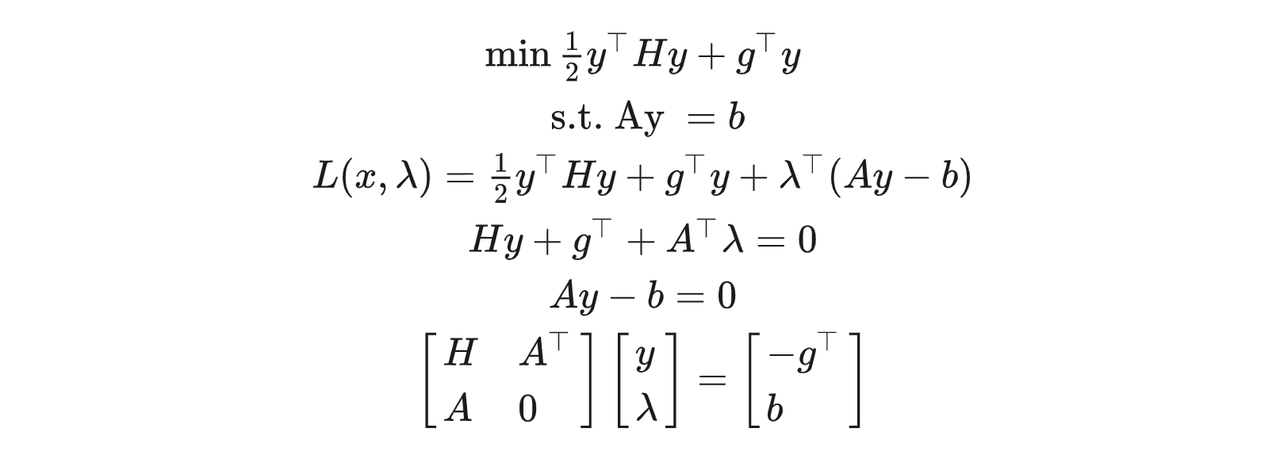
现在考虑具有不等式约束的MPC问题(MPC问题的不等式约束一般是每一个horizon内部的约束):
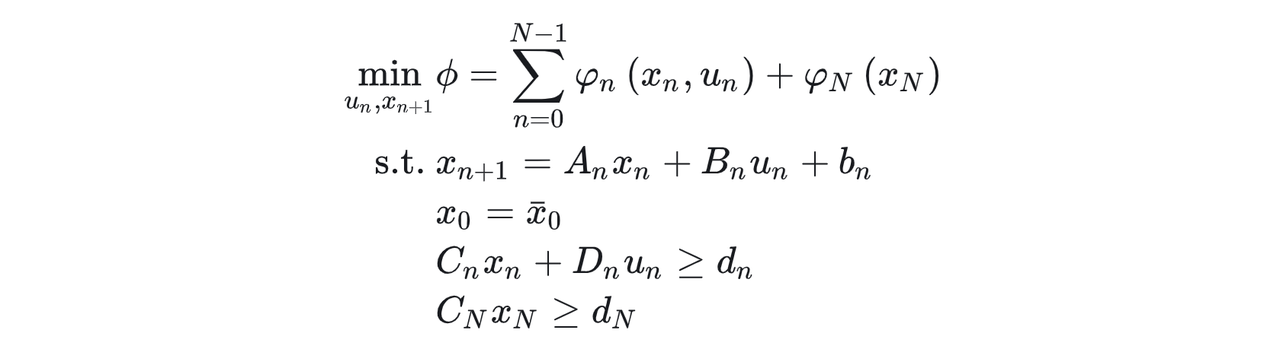
那么我们需要使用内点法不断迭代,求解KKT系统
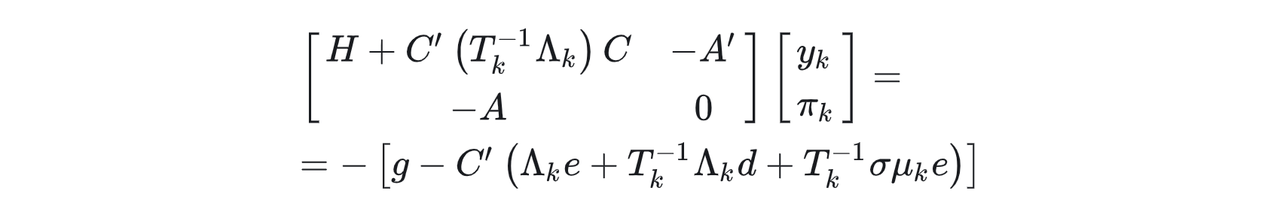
这其实就是和只有线性等式约束MPC问题的KKT系统具有同样的结构,那就可以利用上面的动态规划思路推导的结果去求解这个方程组啦。文章结尾给出了HPMPC算法的数值计算结果,单位都是ms级别:

参考文献
[1] G. Frison, H. H. B. Sørensen, B. Dammann and J. B. Jørgensen, “High-performance small-scale solvers for linear Model Predictive Control,” 2014 European Control Conference (ECC), Strasbourg, France, 2014, pp. 128-133, doi: 10.1109/ECC.2014.6862490.
[2] https://cvxgen.com/docs/index.html
[3] Zanelli, A., Domahidi, A., Jerez, J., & Morari, M. (2017). FORCES NLP: an efficient implementation of interior-point methods for multistage nonlinear nonconvex programs. International Journal of Control, 93(1), 13–29. https://doi.org/10.1080/00207179.2017.1316017
[4] Y. Wang and S. Boyd, “Fast Model Predictive Control Using Online Optimization,” in IEEE Transactions on Control Systems Technology, vol. 18, no. 2, pp. 267-278, March 2010, doi: 10.1109/TCST.2009.2017934.
[5] G. Frison and J. B. Jørgensen, “Efficient implementation of the Riccati recursion for solving linear-quadratic control problems,” 2013 IEEE International Conference on Control Applications (CCA), Hyderabad, India, 2013, pp. 1117-1122, doi: 10.1109/CCA.2013.6662901.



















