上一期我们一起学习了存储问题及其基本概念,本期小编将带大家学习确定型存储模型的相关内容。
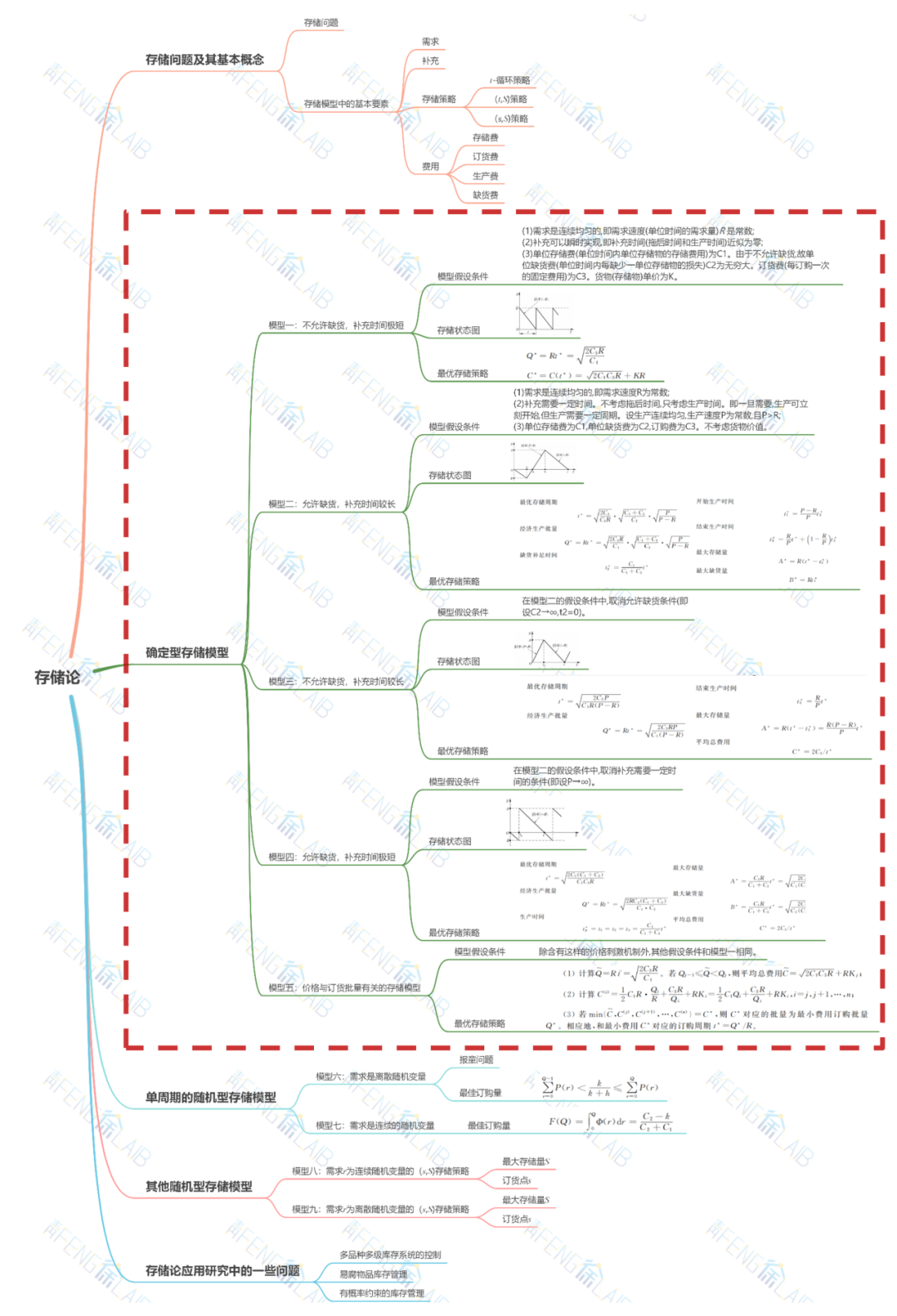
下面我们一起来学习确定型存储模型的五个基础模型吧!
模型一:不允许缺货,补充时间极短
为了便于描述和分析,对模型作如下假设:
(1)需求是连续均匀的,需求速度R为常数;
(2)补充可以瞬时实现,补充时间(拖后时间和生产时间)近似为0;
(3)单位时间内单位存储费为C1;不允许缺货,单位缺货费用C2为无穷大;订货费C3;货物单价为K。
设补充间隔时间为t,补充时存储已用尽,每次补充量为Q,下图为存储状态图。
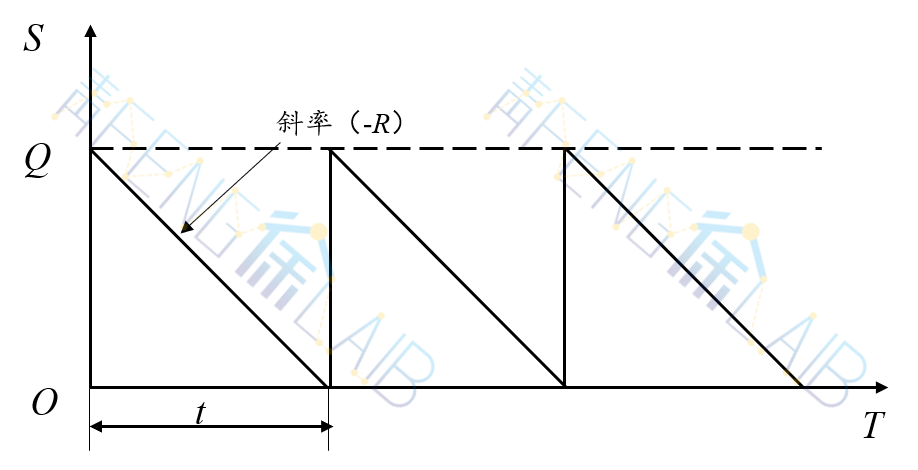
一次补充量Q必须满足t时间内的需求,故Q=Rt。
因此,订货费为
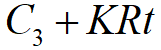
t时间内的平均订货费为
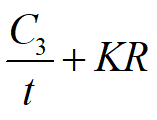
由于需求是连续均匀的,故时间内的平均存储量为
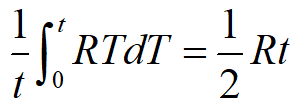
因此, t时间内的平均存储费为
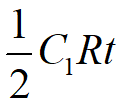
由于不允许缺货,故不考虑缺货费用。故t 时间内的平均总费用为
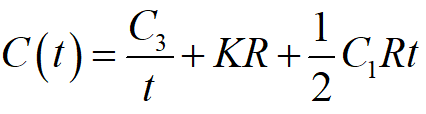
C(t)随t的变化而变化,其图像见下图。当t=t* 时,C(t*)=C* 是C(t)的最小值。

为了求t*,可解
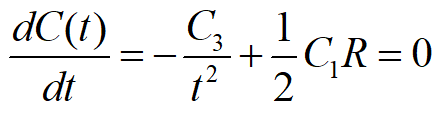
得
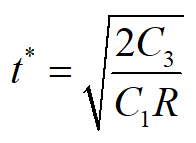
因此,得到每隔时间t*补充存储量Q*为
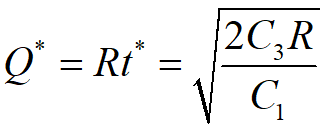
该式被称为经济订购批量公式(EOQ)。
这样平均总费用为
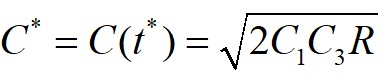
由于存储单价K与补充量Q无关,因此,存储物总价KQ和存储策略的选择无关。因此常将此项省略,得
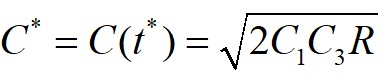
例题展示
例1 某商品单位成本为5元,每天保管费为成本的0.1%,每次订购费为10元。已知对该商品的需求是100件/天,不允许缺货。假设该商品的进货可以随时实现。问应该怎样组织进货,才最经济。
解:由题意可知,本存储问题为不允许缺货,补充时间极短模型;K=5元/件,C1=5×0.1%=0.005元/(件∙天),C3=10元,R=100件/天,将数值代入公式
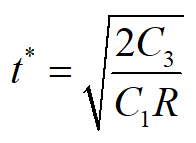
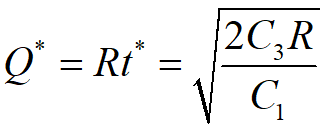
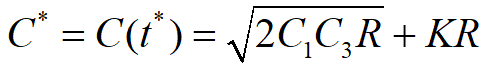
得
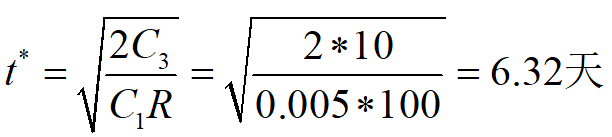
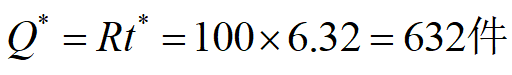
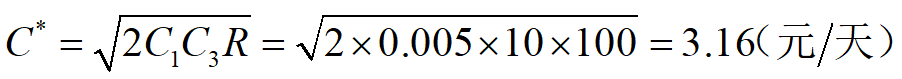
所以应该每隔6.32天进货一次,每次进货该商品632件,能使总费用最少,平均每天3.16元。按年计算则每年进货约,每次进货630件。
模型二:允许缺货,补充时间较长
模型假设条件:
(1)需求是连续均匀的,需求速度R为常数;
(2)补充需要一定时间。不考虑拖后时间,只考虑生产时间。即一旦需要,生产立刻开始,但生产需要一定周期。设生产连续均匀,生产速度P为常数,且 P > R;
(3)单位存储费为C1;单位缺货费用C2;订货费C3。不考虑货物价值。下图是存储状态图。
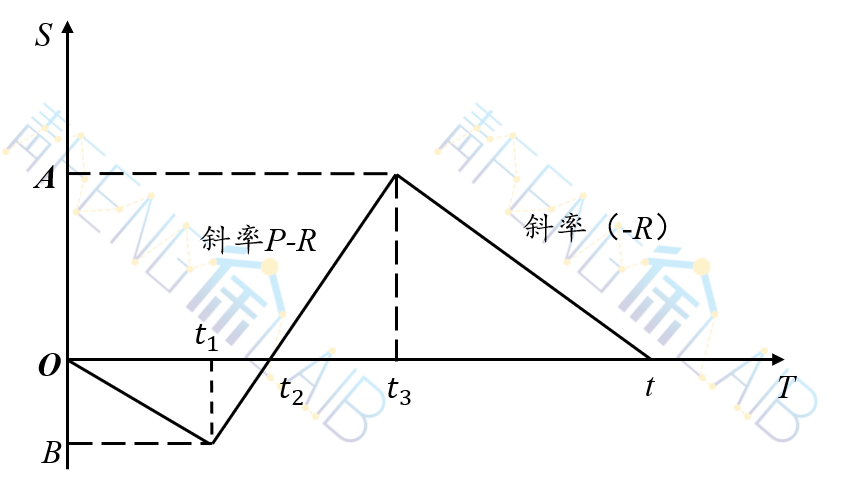
[0,t]一个存储周期,t1时刻开始生产,t3时刻结束生产;
[0,t2]时间内存储为0,t1时刻达到最大缺货量B;
[t1,t2]时间内产量以速度R满足需求,并以速度(P-R)补充[0,t1]时间内得缺货,至t2 时刻缺货补足。
[t2,t3]时间内产量一方面以速度R满足需求,并以速度(P-R)增加存储。至t3 时刻达到最大存储量A,并停止生产。
[t3,t]时间内,存储以速度R减少。至t降为0,进入下一周期。
根据模型假设条件和存储状态图,首先导出[0,t]时间内的平均总费用(即费用函数),然后确定最有存储策略。
从[0,t1]看,最大缺货量B=Rt1;从[t1,t2]看,B=(P-R)(t2-t1),联立可解。
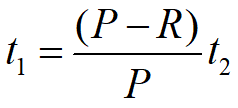
从[t2,t3]看,最大存储量A=(P-R)(t3-t2),从[t3,t ]看,最大存储量A=R(t-t3),联立可解
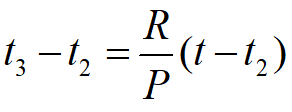
在[0,t]时间内,存储费为
缺货费为
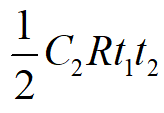
订购费(生产准备费)为C3。
因此,[0,t]时间内平均总费用为:
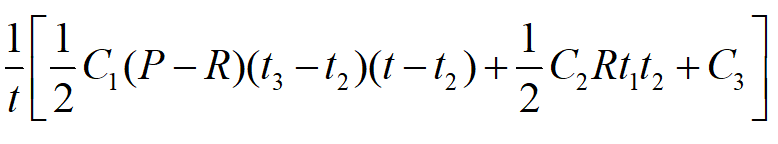
将
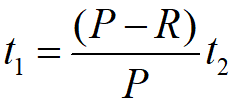
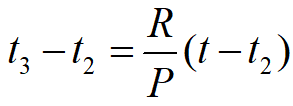
整理得
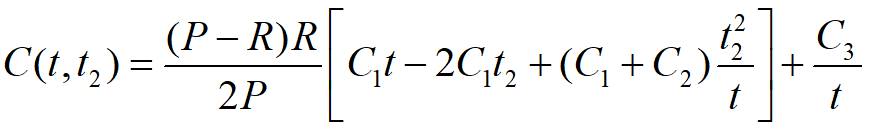
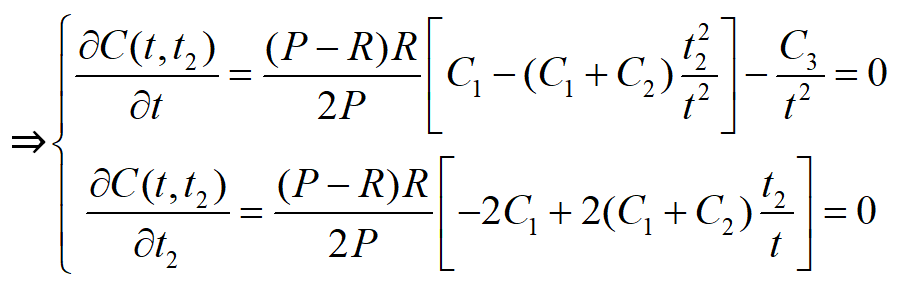
可得
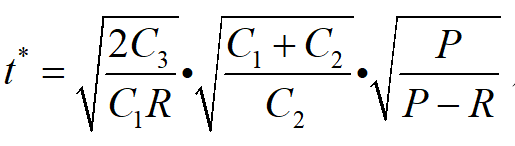
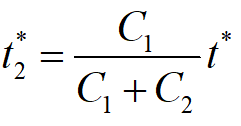
此时费用C(t*,t*2)为最小值。
因此,模型二的最优存储策略各参数值为:
最优存储周期
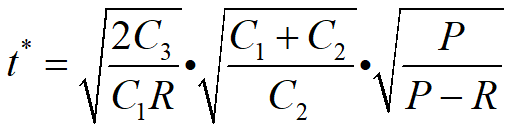
经济生产批量
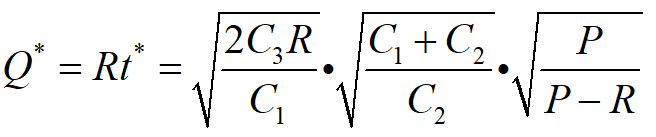
缺货补足时间
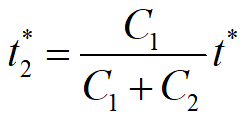
开始生产时间
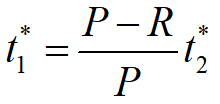
结束生产时间
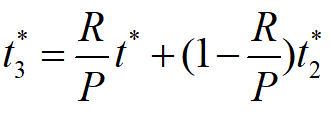
最大存储量
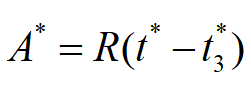
最大缺货量
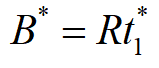
平均总费用
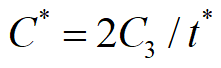
例题展示
例2 企业生产某种产品,正常生产条件下可生产10件/天。根据供货合同,需按7件/天供货。存储费每件0.13元/天,缺货费每件0.5元/天,每件生产准备费用为80元,求最优存储策略。
解:据题意,P=10件/天,R=7件/天,C1=0.13元/(件∙天),C2=0.5元/(件∙天), C3=80元/次。
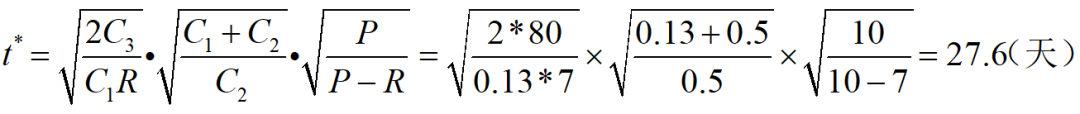
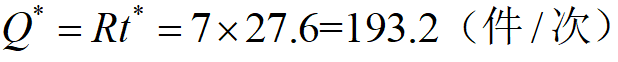
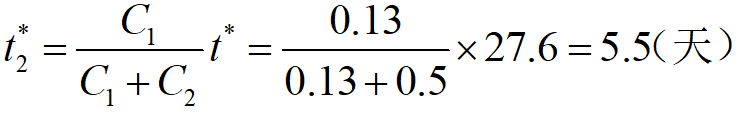
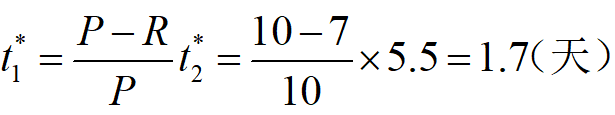
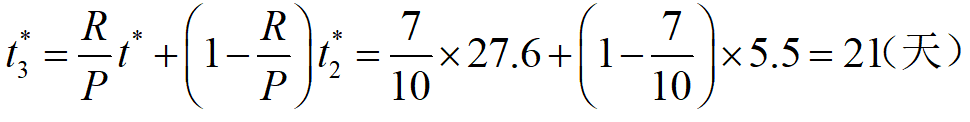
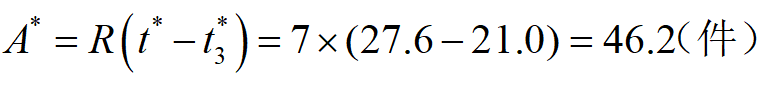
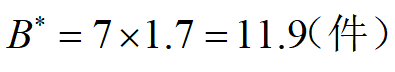
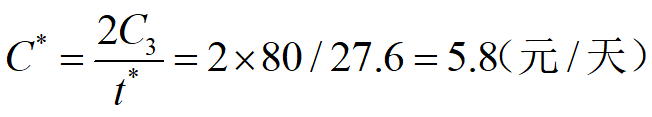
模型三:不允许缺货,补充时间较长
模型三的存储状态图见下图,在模型二的假设条件中,允许缺货条件(即设C2→∞,t2=0),就成为模型三。
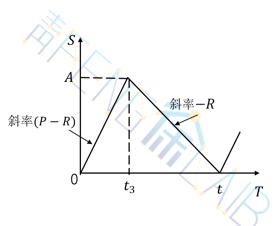
因此,模型三的最优存储策略各参数:
最优存储周期
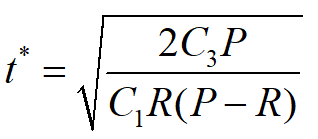
经济生产批量
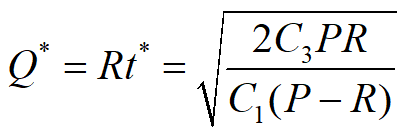
结束生产时间
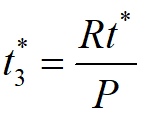
最大存储量
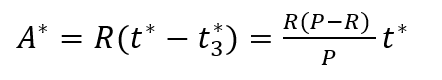
平均总费用
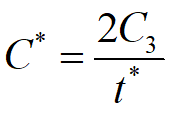
例题展示
例3 商店经销某商品,月需求量为30件,需求速度为常数。该商品每件进价300元,月存储费为进价的2%。向工厂订购该商品时订购费每次20元,订购后需5天才开始到货,到货速度为常数,即2件/天。求最优存储策略。
解:订购时间为存储为0的前5天。拖后时间为[0,t0],存储量为L=Rt0 ;据题意P=2件/天,R=1件 /天,C1=300×2%×1/30=0.2 /天·件,C3=20/次,t0 =5天,L=1×5=5件 。代入前述公式可解得
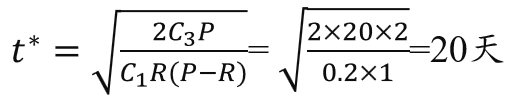
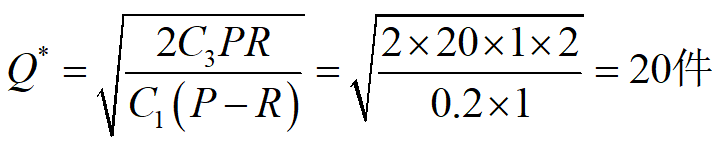
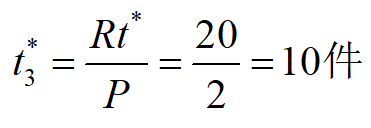
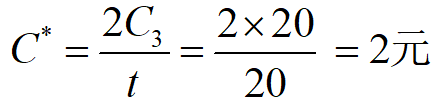
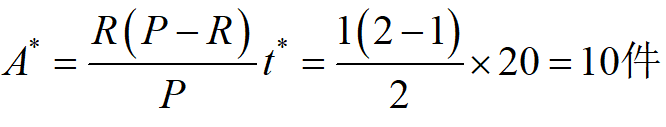
模型四:允许缺货,补充时间极短
模型四的存储状态图见下图。在模型二的假设条件中,取消补充需要一定时间的条件(即设P→∞),就成为模型四。

因此模型四的最优存储策略各参数:
最优存储周期
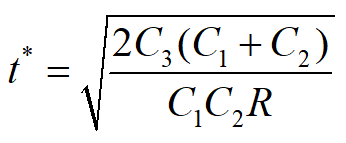
经济生产批量
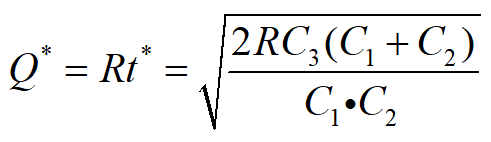
生产时间
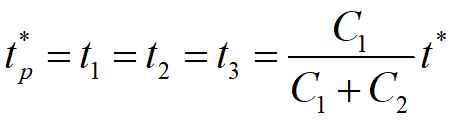
最大存储量
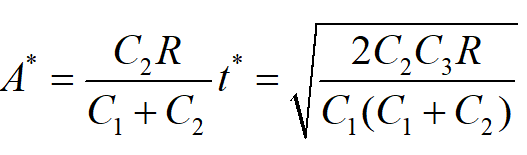
最大缺货量
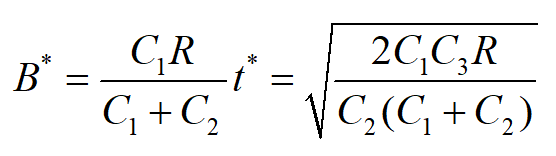
平均总费用
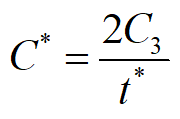
对于确定型存储问题,上述四个模型是最基本的模型。其中模型二是最基础的模型,模型一、三、四为模型二的特殊情况。在每个模型的最优存储模型的各个参数中,t*为最基本参数,各模型中各个参数与t*的关系均相同。因子
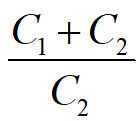
为是否允许缺货的假设条件,因子
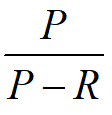
为补充是否需要时间的假设条件。
模型五:不允许缺价格与订货批量有关的存储模型
为了鼓励大批量订货,供方常对需方实行价格优惠。订货批量越大,货物价格越便宜。模型五的模型假设除了价格与订货批量相关这一条件之外,其他假设条件与模型一相同,即需求是连续均匀的,需求速度R为常数;充可以瞬时实现,补充时间(拖后时间和生产时间)近似为0;位时间内单位存储费C1;为不允许缺货,单位缺货费用C2为无穷大;订货费C3;货物单价为K。
设订货批量为Q,对应的货物单价为K(Q)。当
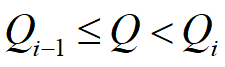
时,K(Q)=K(i=1,2,...,n)
其中,Qi 为价格折扣的某个分界点,且
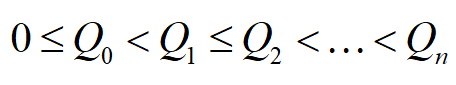
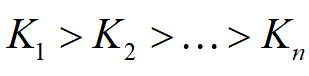
根据模型一的
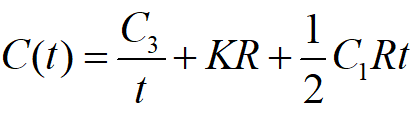
得到模型五的平均总费用
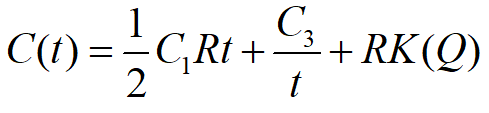
其中,Q=Rt。当
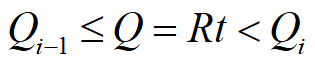
时,
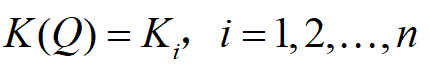
C(t)关于t的分段函数。以n=3为例,画出图像,见下图。
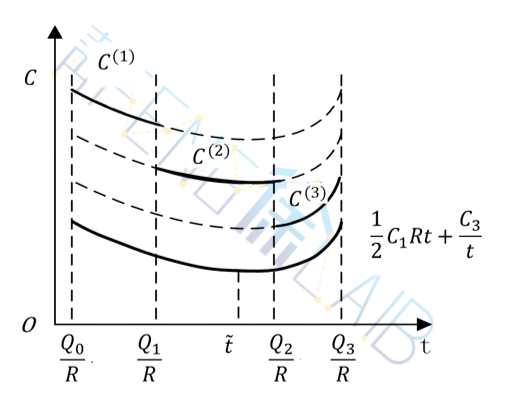
如果不考虑货物总价RK(Q),则最小费用点为
![]()
考虑货物总价时,费用曲线呈逐段递减趋势,故
![]()
不一定是最小费用点。
确定最小平均总费用订购批量的步骤:
计算
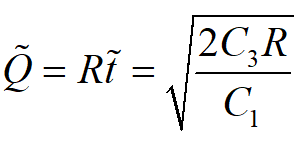
若
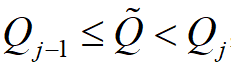
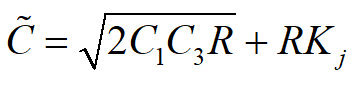
计算
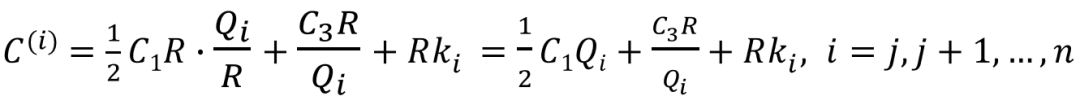
若
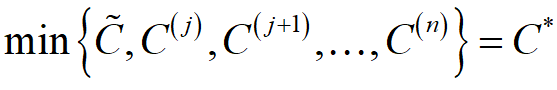
则对应的批量为最小费用订购批量Q*。相应的,对应的订购周期t*=Q*/R。
例题展示
例4 工厂每周需要零配件32箱,存储费每箱每周1元,每次订购费25元,不允许缺货。零配件进货时若:(1)订货量1~ 9箱时,每箱12元,(2)订货量10 ~ 49箱时,每箱10元: (3)订货量50 ~ 99箱时,每箱9.5元,(4)订货量100箱及以上时,每箱9元。求最优存储策略。
解:
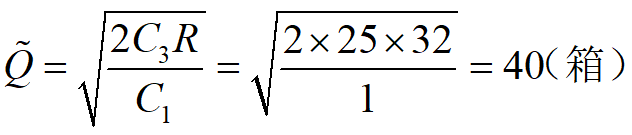
因在10~49格为K2=10元,平均总费用
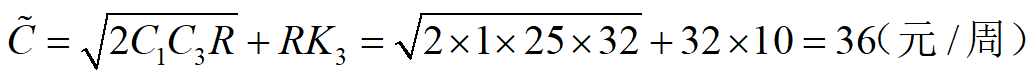
又因为
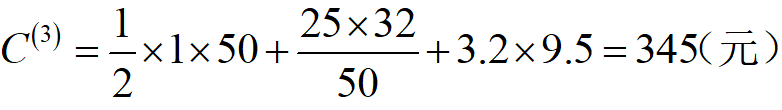
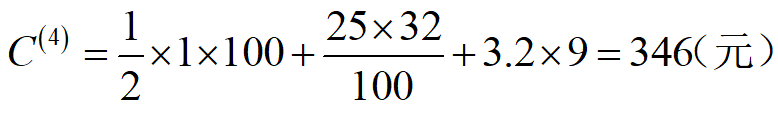
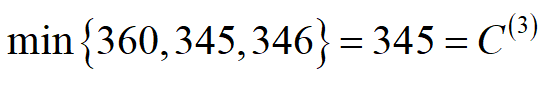
故最优订购批量Q*=50箱,最小费用C*=345元/周,订购周期
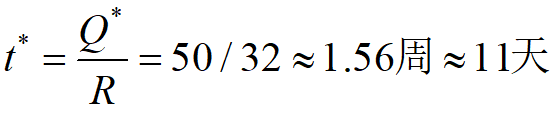
上述五个模型的最优存储周期、最佳存储批量、最小平均总量、最大存储量和最大缺货量五个参数的对比表如下所示。
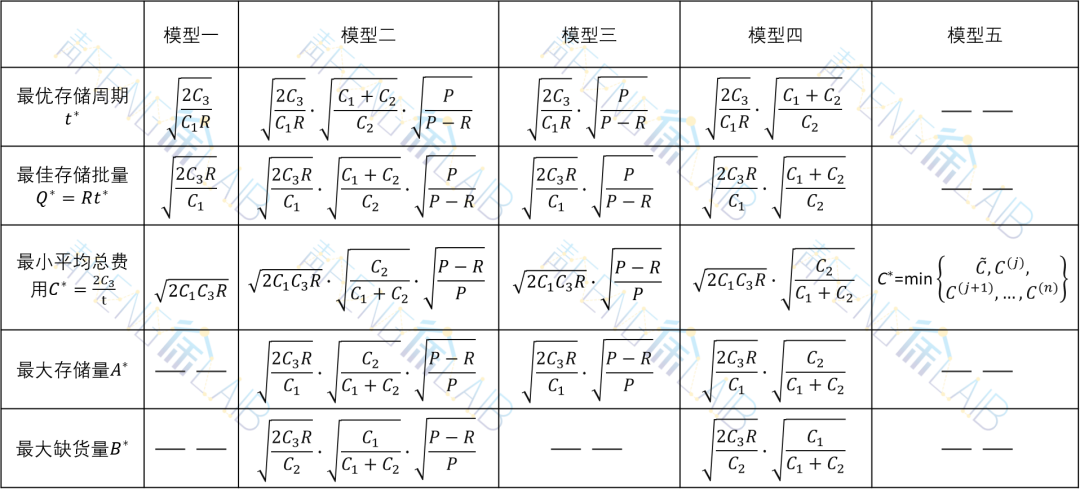
以上就是确定型存储模型的全部内容了,通过这一节的学习,大家可以尝试对现实生活中的一些实际问题进行练习了!