特征构造(Feature Engineering)
特征构造是从现有数据中创建新的特征,以揭示数据中的隐藏关系,从而提高模型表现。这是数据预处理中一个关键步骤,可以显著提升模型的性能。
原理
通过特征构造,我们可以利用现有特征之间的关系来创建新的特征。例如,对于两个特征 x1 和 x2,我们可以构造它们的交互特征 x1× x2:
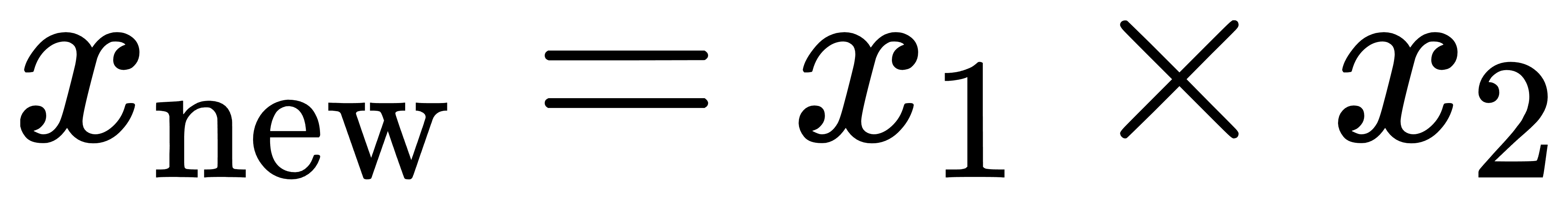
此外,可以使用各种数学运算、统计量或领域知识来构造新的特征,以揭示数据中的隐藏关系。
案例:在线购物平台数据
假设我们有一个在线购物平台的用户行为数据集,其中包含用户的基本信息和购买行为数据,如访问次数、购买次数、平均购买金额等。我们将通过特征构造,创建一些新的特征,如每次访问的平均购买金额和购买率,并进行可视化分析。
数据描述
user_id:用户IDvisits:访问次数purchases:购买次数total_spent:总消费金额
Python代码
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 生成示例数据
np.random.seed(42)
data = pd.DataFrame({
'user_id': range(1, 101),
'visits': np.random.randint(1, 20, 100),
'purchases': np.random.randint(0, 10, 100),
'total_spent': np.random.uniform(10, 1000, 100)
})
# 构造新特征
data['avg_spent_per_visit'] = data['total_spent'] / data['visits']
data['purchase_rate'] = data['purchases'] / data['visits']
# 显示前几行数据
print("数据集前几行:")
print(data.head())
# 绘制图形
plt.figure(figsize=(14, 6))
# 图形1:每次访问的平均购买金额与总消费金额的关系
plt.subplot(1, 2, 1)
sns.scatterplot(x=data['avg_spent_per_visit'], y=data['total_spent'])
plt.title('Avg Spent per Visit vs Total Spent')
plt.xlabel('Avg Spent per Visit ($)')
plt.ylabel('Total Spent ($)')
# 图形2:购买率与总消费金额的关系
plt.subplot(1, 2, 2)
sns.scatterplot(x=data['purchase_rate'], y=data['total_spent'])
plt.title('Purchase Rate vs Total Spent')
plt.xlabel('Purchase Rate')
plt.ylabel('Total Spent ($)')
plt.tight_layout()
plt.show()
# 更多图形
plt.figure(figsize=(14, 6))
# 图形3:访问次数与总消费金额的关系
plt.subplot(1, 2, 1)
sns.scatterplot(x=data['visits'], y=data['total_spent'])
plt.title('Visits vs Total Spent')
plt.xlabel('Visits')
plt.ylabel('Total Spent ($)')
# 图形4:每次访问的平均购买金额的分布
plt.subplot(1, 2, 2)
sns.histplot(data['avg_spent_per_visit'], kde=True)
plt.title('Distribution of Avg Spent per Visit')
plt.xlabel('Avg Spent per Visit ($)')
plt.ylabel('Frequency')
plt.tight_layout()
plt.show()代码解析
- 生成示例数据:创建一个包含用户访问和购买行为的示例数据集,包括用户ID、访问次数、购买次数和总消费金额。
- 构造新特征:
-
avg_spent_per_visit:每次访问的平均购买金额,通过总消费金额除以访问次数计算得到。purchase_rate:购买率,通过购买次数除以访问次数计算得到。
- 显示前几行数据:输出数据集的前几行,以便检查数据和新特征的正确性。
- 绘制图形:
-
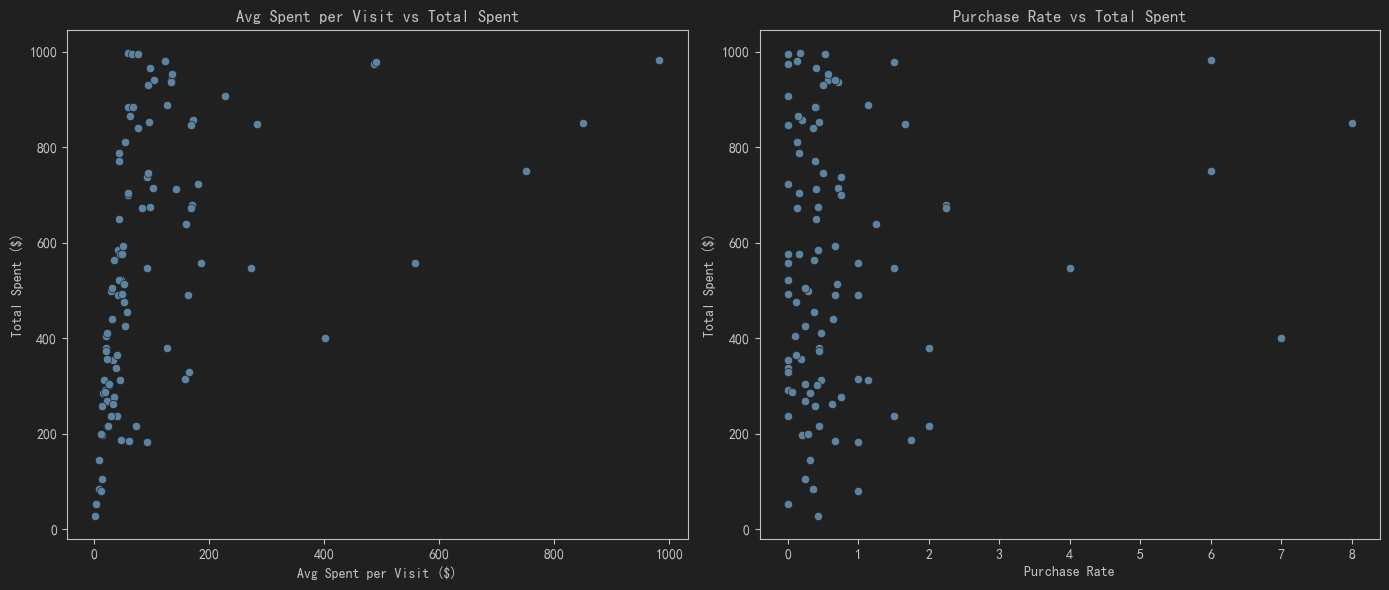
- 图形1:展示每次访问的平均购买金额与总消费金额的关系。使用散点图来观察不同用户的购买行为。
- 图形2:展示购买率与总消费金额的关系。使用散点图来观察购买率对总消费金额的影响。
-
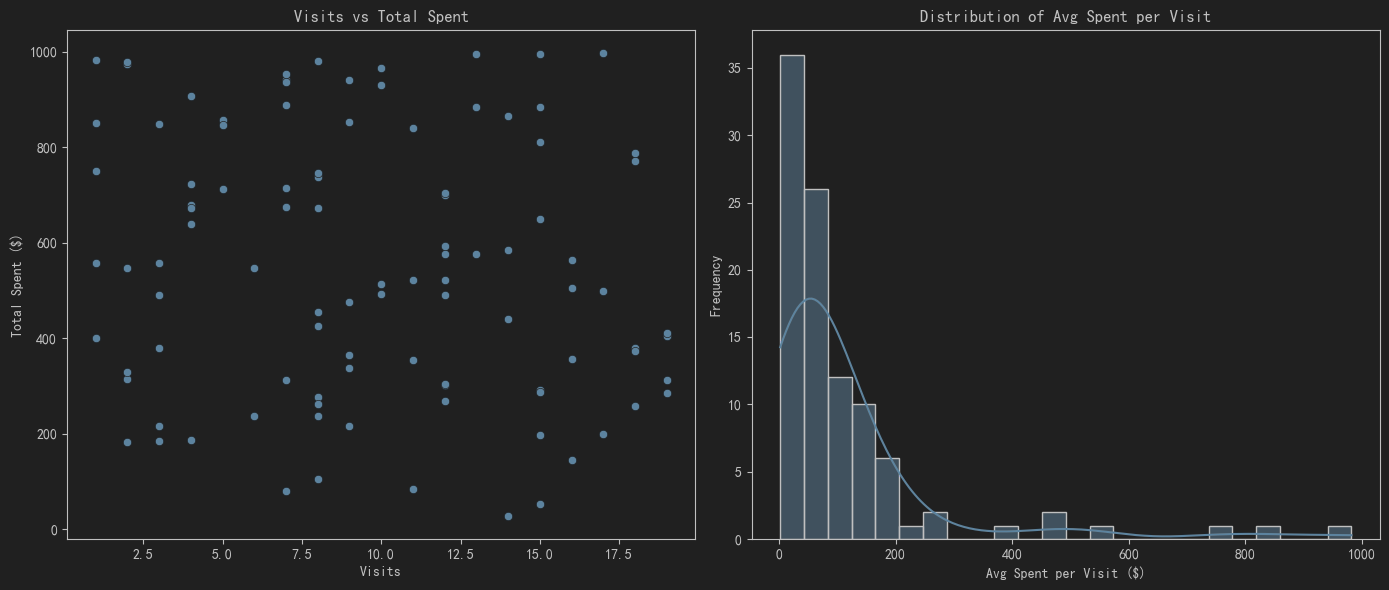
- 图形3:展示访问次数与总消费金额的关系。使用散点图来观察不同访问次数用户的消费情况。
- 图形4:展示每次访问的平均购买金额的分布。使用直方图和核密度估计(KDE)来观察每次访问的平均购买金额的分布情况。
通过这个生活场景的案例,我们可以看到特征构造如何揭示数据中的隐藏关系,并帮助我们更好地理解和分析数据。构造的新特征不仅可以提高模型的表现,还可以为数据分析提供更多有价值的视角。
降维(Dimensionality Reduction)
降维是减少特征数量的技术,旨在保留数据的主要信息。常用的方法包括主成分分析(PCA)和线性判别分析(LDA)。通过降维,可以减少数据的复杂性,消除噪声,并提高模型的性能。
原理
- 主成分分析(PCA):
-
- 数据中心化:将数据集的每个特征减去其均值。
- 计算协方差矩阵:描述数据的协方差信息。
- 特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量。
- 选择前k个最大特征值对应的特征向量构成变换矩阵。
- 变换数据:用变换矩阵将原始数据投影到低维空间。
核心公式:
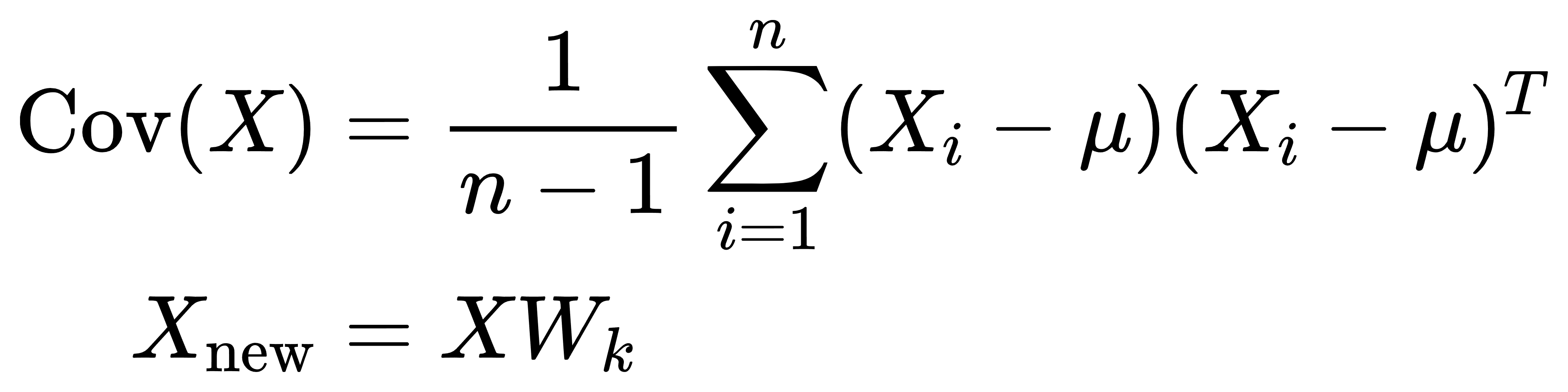
案例:客户购买行为数据
假设我们有一个大型超市的客户购买行为数据集,其中包含多个特征,如客户年龄、月均购买次数、月均消费金额、购买种类数等。我们将通过PCA和t-SNE降维方法,将数据从高维降到二维,以便可视化分析。
数据描述
customer_id:客户IDage:年龄avg_purchases_per_month:月均购买次数avg_spent_per_month:月均消费金额purchase_variety:购买种类数
Python代码
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.decomposition import PCA
from sklearn.manifold import TSNE
# 生成示例数据
np.random.seed(42)
data = pd.DataFrame({
'customer_id': range(1, 101),
'age': np.random.randint(18, 70, 100),
'avg_purchases_per_month': np.random.randint(1, 30, 100),
'avg_spent_per_month': np.random.uniform(100, 5000, 100),
'purchase_variety': np.random.randint(1, 20, 100)
})
# 提取特征列
features = data[['age', 'avg_purchases_per_month', 'avg_spent_per_month', 'purchase_variety']]
# 使用PCA将数据降到2维
pca = PCA(n_components=2)
data_pca = pca.fit_transform(features)
# 使用t-SNE将数据降到2维
tsne = TSNE(n_components=2, random_state=42)
data_tsne = tsne.fit_transform(features)
# 绘制PCA降维后的数据
plt.figure(figsize=(14, 6))
plt.subplot(1, 2, 1)
scatter = plt.scatter(data_pca[:, 0], data_pca[:, 1], c=data['age'], cmap='viridis', alpha=0.7)
plt.colorbar(scatter, label='Age')
plt.title('PCA of Customer Data')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
# 绘制t-SNE降维后的数据
plt.subplot(1, 2, 2)
scatter = plt.scatter(data_tsne[:, 0], data_tsne[:, 1], c=data['age'], cmap='viridis', alpha=0.7)
plt.colorbar(scatter, label='Age')
plt.title('t-SNE of Customer Data')
plt.xlabel('t-SNE Component 1')
plt.ylabel('t-SNE Component 2')
plt.show()
# 计算PCA的前两个主成分的解释方差比
explained_variance = pca.explained_variance_ratio_
print(f'Explained variance by the first two principal components: {explained_variance[0]:.2f}, {explained_variance[1]:.2f}')
# 用Seaborn绘制Pairplot图(可以绘制更多维度,但这里只选前两个维度示范)
df_pca = pd.DataFrame(data_pca, columns=['PC1', 'PC2'])
df_pca['age'] = data['age']
sns.pairplot(df_pca, hue='age', palette='viridis')
plt.suptitle('Pairplot of PCA Components', y=1.02)
plt.show()代码解析
- 生成示例数据:创建一个包含客户购买行为的示例数据集,包括客户ID、年龄、月均购买次数、月均消费金额和购买种类数。
- 提取特征列:从数据集中提取用于降维的特征列。
- 使用PCA降维:将数据降到二维,方便可视化分析。绘制PCA降维后的散点图,以客户年龄为颜色。
- 使用t-SNE降维:同样将数据降到二维,并绘制t-SNE降维后的散点图,以客户年龄为颜色。
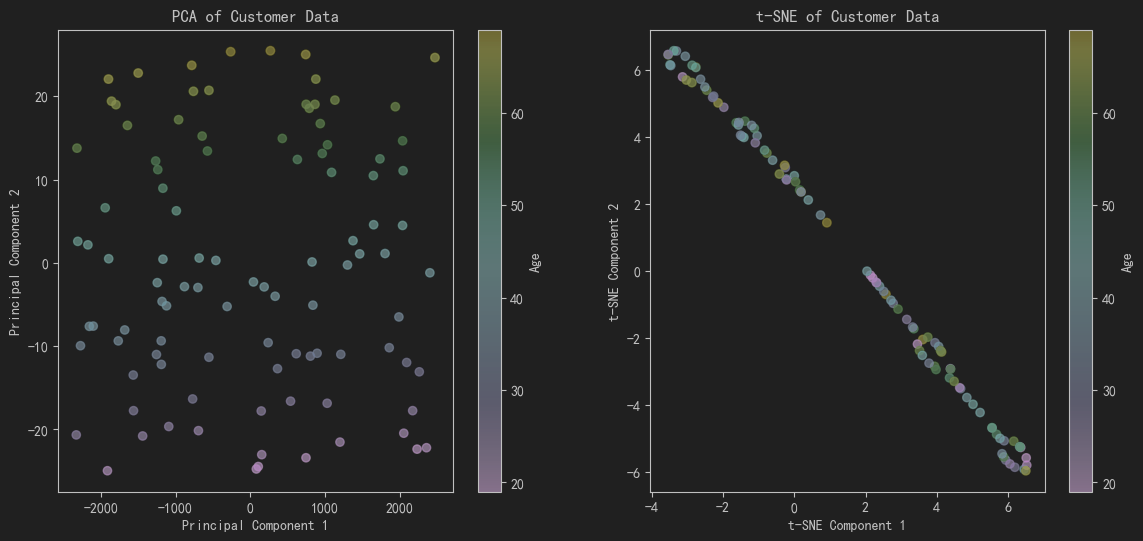
- 解释方差比:计算PCA前两个主成分的解释方差比,展示降维后的信息保留程度。
- 绘制Pairplot图:使用Seaborn绘制PCA主成分的成对关系图,以客户年龄为颜色。
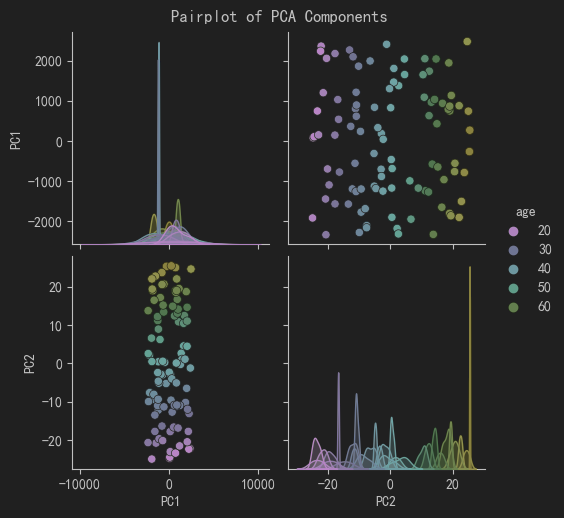
通过这个生活场景的案例,我们可以看到降维如何帮助我们减少数据的复杂性,同时保留主要信息,从而更好地理解和分析数据。