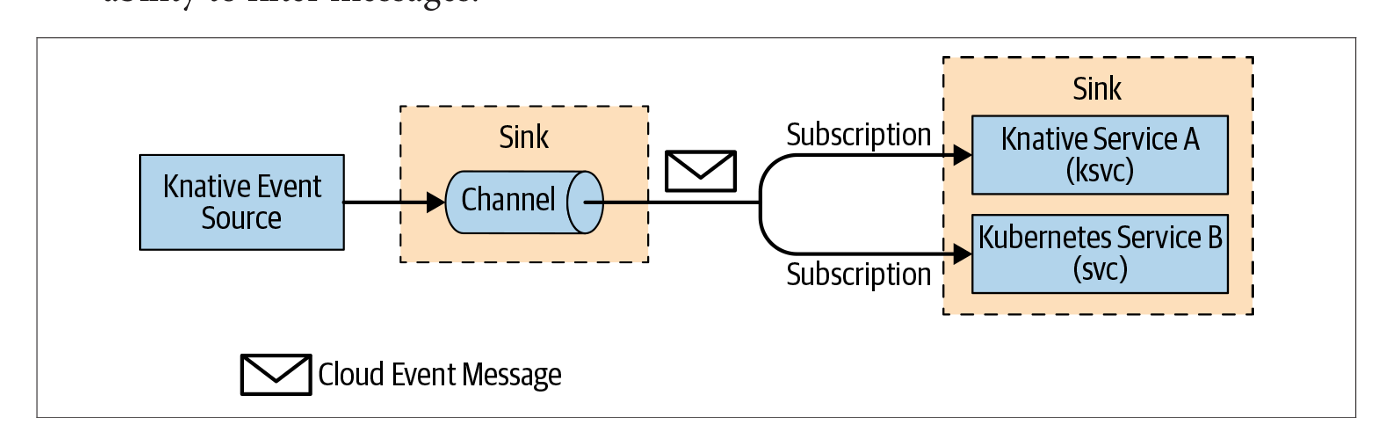
​
图片来源：
https

​一、说明

虽然物理学引起了公众的好奇心，但许多人发现数学令人生畏。然而，物理学中的许多中心思想都源于更简单的原理，这些原理已被调整和修改为越来越复杂的形式主义，从而更好地映射物理现象。

虽然许多物理学毕业生最终从事数据科学工作，但物理学中的数学见解能否为数据科学家提供信息和丰富？我认为是的。尽管数据科学作为一门独特的学科是相对论的新学科，但数据的收集和分析贯穿了物理学史，例如约翰内斯·开普勒（Johannes Kepler）收集的天文观测，他从中得出了行星运动定律。物理学和数据科学都从数据中提取模式，尽管通常数据科学处理的是统计模式，而物理学则处理合法或命名模式。了解基本定律可以帮助数据科学家对复杂系统进行建模，并开发对现实世界现象的模拟。

在我自己的工作中，保持对物理学的浓厚兴趣帮助我在信息论和统计力学之间建立了重要的联系。此外，它帮助我理解了数学的灵活性，特别是线性代数和微积分，在建模受空间维度约束的物理系统和包括社会和随机模式在内的更抽象的多维系统时。此外，了解物理学如何模拟我们周围世界的雏形，以及物理学的逐步改进如何需要塑造数学以拟合和预测大自然提供的数据，这在智力上是令人鼓舞的，也是令人欣慰的。

在这篇文章中，我通过三个数学思想进行了探索，这些思想支撑着物理学的大部分：稳态作用原理（也称为最小作用原理）、洛伦兹变换（描述了爱因斯坦狭义相对论中的时间和空间变换）和度量张量，它是广义相对论（引力理论作为时空曲率）数学的基础。

稳态作用原理可能是所有物理学中最重要的原理，因为它贯穿了经典力学和量子力学。它形成了牛顿发明的用于描述物理系统演化的经典运动方程的替代形式，尽管等同于经典运动方程。具体来说，它通过确定最小化称为动作的东西的路径来描述物理系统在时间上的运动。该动作是一个函数，即一个将函数作为输入的函数，它将系统的路径描述为相对于两点之间的路径变化是静止的。将动作理解为函数，特别是对路径变化进行评分，是理解其背后概念的关键。具体细节将在下面的阐述中变得更加清晰。这一显著的结果将运动表达为给定约束条件下的一种优化函数。

洛伦兹变换描述了时间和空间坐标如何交织成一个统一的度量，这使得它们的测量值相对于惯性参考系中的观察者成比例地变化，同时保持光速。这种形式主义确保了光速在参考系上保持恒定，这与牛顿的假设相反，牛顿的假设是光速相对于空间和时间的不变单位而变化。在狭义相对论之前，光速的恒定性是一种实验观察到的现象，不符合经典物理学的框架。

最后，我们解释了度量张量背后的数学思想，度量张量描述了弯曲空间中的长度或距离。度量张量是一个双线性对称单位矩阵，它将平坦欧几里得空间下的勾股定理推广到任何可能的空间，包括曲面。爱因斯坦使用曲面来描述在引力存在下时空的扭曲。作为数据科学家，您可能非常熟悉欧几里得距离和线性代数，因此理解度量张量背后的概念应该是一个自然而然的步骤。伯恩哈德·黎曼（Bernhard Riemann）开发的度量张量构成了非欧几里得几何的基础，并显着地将长度概念推广到任何基础几何。

二、最小行动原则

要开始理解这一原理，回想一下牛顿第二定律通过三个输入来计算粒子系统的轨迹：粒子的质量、作用在系统上的力以及初始位置和速度，并通过 F=马 确定演化规则，其中 m 表示质量和加速度。与牛顿方法相比，最小作用原理通过考虑初始和最终位置、质量和速度（以及取决于系统的其他约束）来计算系统的轨迹，但省略了力。随后，它选择最小化称为动作的数量的路径。在我们确切解释作用由什么组成之前，我们需要了解牛顿方程的另一种公式，称为拉格朗日方程。

拉格朗日量 L 计算为动能 T 和势能 V 之间的差值，其中 T 由质量和速度的乘积除以 2（2 表示初始速度和最终速度之间的平均值）给出，V 由物体质量 m 的乘积给出，引力常数 g 以及物体离地面 h 的高度（势能的计算随系统而变化）。

为什么拉格朗日量被计算为动能和势能之间的差值？因为当系统移动时，它会将势能转化为动能，而两者之间的差异捕捉到了这两种能量之间的动态相互作用。相反，重要的是要注意，总能量是计算为这两个值的总和。

拉格朗日量的输入是位置 x 和速度 v，用 ⨰ （x 点） 表示，其中点表示一阶导数。这是因为速度是作为位置的一阶导数计算的。

为了计算拉格朗日量，我们需要至少知道粒子的速度、一般坐标、位置和质量。势能取决于粒子（或粒子组）的位置，因为它描述了它可以做的势功，而动能取决于粒子速度，因为它描述了粒子的运动。

动作是如何出现的？想象一下，在一个弯曲的平面上有两个点，你需要找到最短的距离。两点之间有许多路径，但只有一条路径或线表示最短的距离。该操作类似于此问题。为了找到系统的轨迹，我们需要选择一条最小化动作的路径。由此得出的推论是，在系统的演变过程中，动作保持静止。

由于动作必须是平稳的，因此动作的一阶偏导数必须为零：

在高层次上，动作由给定时间间隔 [t₀， t₁] 的拉格朗日路径积分描述。尽管从点 t₀ 到 t₁ 的函数积分通常被理解为曲线下的面积，但拉格朗日量的路径积分不应直观地视为一个面积，而应视为一个函数的积分，该函数是一个将另一个函数作为输入并输出标量的函数。输入将是拉格朗日量。输出定义操作。在系统可能在 t₀ 和 t₁ 之间采取的许多路径中，我们将看到它所采用的正是最小化动作的路径。

以下是作为拉格朗日路径积分的动作的简单公式：

​
现在，由于定积分可以计算为 f（x） 的 y 输出和 Δx 表示的 x 变化的黎曼和，当 k 面积划分接近无穷大时，我们可以将作用计算为拉格朗日和时间导数 dt 的乘积的黎曼和。换句话说，拉格朗日量的定积分可以通过最小化时间间隔内的动作来计算。

该动作由系统初始位置和最终位置之间的拉格朗日路径积分组成。这意味着路径积分通过计算势能和动能之间的差值来最小化作用。微积分的基本定理允许我们将动作计算为 t₀ 和 t₁ 之间的连续间隔，即使它也可以在离散时间步长 N 中计算。现在，如果我们将动作想象为离散时间步长 N 的总和，我们会将其计算为每个时间步长的拉格朗日量值与时间 t 值的乘积之和。

拉格朗日量通常取决于位置和速度，但也可能与时间有关。如果拉格朗日量随时间变化，即使它的位置和速度保持不变，它也被认为是时间依赖的。否则，拉格朗日量通过改变位置和速度隐含地依赖于时间。对于与时间无关的公式，我们将 L（x，⨰ ） 代入方程中，以表示对位置和速度的依赖性：

​
现在，我们从动量守恒定律中知道，系统所有动量之和的导数等于零。换句话说，在一个孤立的系统中，总动量总是守恒的或保持不变的。常数的导数为零，因为变化率保持在同等或相等的状态。在牛顿力学中，第三运动定律指出，对于每个动作，都有一个相反且相等的反应，表达了总动量守恒。

同样，能量守恒定律认为，在任何变换中，孤立系统的总能量都是守恒的：总能量的时间导数为零。然而，与动量不同的是，能量以不同的形式出现。它是所有这些形式的总和被守恒的。从运动的角度来表达，只有我们一直在谈论的能量形式：动能和潜力。

由于拉格朗日量被定义为这两种能量形式的差异，因此当拉格朗日量在时间平移下不变时，它意味着能量守恒。

与能量守恒有关的事情发生在行动方面。在有符号轨迹中，自然会选择最小化动作值的路径。这种最小化类似于优化问题中函数的最小化，不同之处在于该动作表示大量变量，包括每个时刻的所有坐标。这种极端化特征由欧拉-拉格朗日方程表示，该方程构成了运动方程。

什么是欧拉-拉格朗日方程？它们是微分方程，告诉系统如何从一个时刻移动到下一个时刻。现在，我不打算在这里推导方程，但直观地，我们将把作用 ∂A 相对于位置 dx 的导数设置为 0。换言之，我们考虑路径中的微小变化，并要求动作的偏导数为零。

这产生了欧拉-拉格朗日方程的两个项：拉格朗日量偏导数相对于速度的时间导数，以及拉格朗日量相对于位置的偏导数。它们分别代表动能（动量变化）和势能的变化。将这两个量之间的差值设置为零，可产生最小化欧拉-拉格朗日方程的作用。

下面给出了单个坐标或自由度中的欧拉-拉格朗日方程，其中 L 表示拉格朗日方程、ẋ 速度和 x 位置。

在自然语言中，这理解为拉格朗日量相对于速度 （∂L/∂ẋ） 的偏导数的时间导数 （d/dt） 减去拉格朗日量相对于位置 （∂L/∂x） 的偏导数等于零。直观地说，这可以改写为拉格朗日量相对于速度的瞬时变化率减去拉格朗日量相对于位置的瞬时变化率的瞬时时间变化率是静止的。

进一步提炼，欧拉-拉格朗日方程意味着物理系统的运动对应于拉格朗日积分的极值，即作用。

该方程可以推广到任意坐标（x、y、z…n) :

在具体场景中，动作是函数，也就是说，函数的函数涉及从函数输入（拉格朗日量）到标量输出（动作的值）的映射。

虽然稳态动作原理可以有效地计算物理系统的轨迹，但它需要知道开始和结束位置。取而代之的是这种全局图景，我们用牛顿形式主义代替了牛顿形式主义，它要求知道粒子的位置和初始速度。

稳态作用原理可以适用于量子物理学，但有一些重要的注意事项，其中考虑了初始状态和最终状态之间的所有可能路径，并且作用采用每条路径的概率幅度之和来计算系统的概率演变。

鉴于这个公式，经典的稳态动作原理可以被认为是量子公式的一个特例，其中给定所有路径，稳态动作路径占主导地位。

三、洛伦兹变换

《理解洛伦兹变换》是通往爱因斯坦狭义相对论的门户。它们构成了在惯性或均匀参考系（即排除引力的参考系）中计算相对论时空变换的数学框架。

狭义相对论核心的一个关键概念是，运动只能根据某个参考系来描述，而不是绝对地描述。例如，如果我开车，我相对于汽车静止不动，但相对于我的房子却在移动。

相对论运动的概念存在于经典力学中，最早是由伽利略描述的。

狭义相对论中嵌入的开创性见解不是相对论运动，而是在空间平移中保持不变或不变的东西。在经典力学中，所有运动都是不加区分的相对的，而空间和时间的坐标只是以相加的方式变化，同时保持静态并且对于所有观察者来说都是相互独立的。

经典力学中的相对运动假设意味着光的运动应该服从相对论定律。换句话说，如果我站着不动，拿着手电筒，而你开车拿着手电筒，你的手电筒的光运动应该测量为光速和你的速度之和。

然而，实验证据与这一假设相矛盾。实际上，无论参考系如何，光都是一个常数。换句话说，经验证据证明光速是绝对的。

爱因斯坦没有发现观察的错误，而是将光速的恒定性视为自然定律。如果光的测量结果总是相同的，那么必须改变的是空间和时间坐标的表示。

为了理解爱因斯坦的狭义相对论是如何实现这一点的，粗略地掌握经典力学所描述的简化运动方程是很重要的。这些将被修改，以便观察者之间的相对运动不会改变光速，而是改变空间和时间的交织度量。这有一个特殊的后果，即当速度接近光速极限时，时间和距离的测量值在观察者之间会有所不同。

运动方程通常被浓缩为首字母缩略词 SUVAT（s = 距离，u = 初始速度，v = 速度，a = 加速度，t = 时间）：
​

四、Minkowski 公制

为了使洛伦兹变换易于理解，我们将使用时空图。它们反转距离和时间的轴，使时间表示为 x 轴，距离表示为 y 轴。此外，我们使用 y 轴来表示大距离间隔，因为我们想要解释相对于光速的运动。现在光的传播速度为 3 *10⁸ m/s²。在我们的时空图中，一秒将恰好对应于这个距离。其结果是，我们图的直线对角线位于轴之间 45⁰ 的角度，代表了光速随时间变化的恒定性。事实上，横跨笛卡尔网格的对角线将代表光速的渐近极限，这将限制我们在 y 轴上的时间平移和在 x 轴上的空间平移。

现在，任何与我们的笛卡尔网格对角线不成 45⁰ 角的直线都将表示亚光速下的匀速运动。在牛顿的图景中，光速就像任何其他速度一样。这意味着大于 45⁰ 的钝角将代表比光速更快。此外，光速将相对于参考系。如果我以半光速在与光相同的方向上行进，从我的参考系来看，我会观察到光以半光速运动，因为我正在以它的一半速度赶上它。该模型的假设涉及保持不变的时间和距离单位，以便时间和空间间隔在所有参考系中保持不变。

从将空间和时间视为独立的度量到将它们整合到一个称为时空的连续统一体中的飞跃，涉及将时间变量转换为距离的度量。我们通过将时间变量与 c 加权来做到这一点，c代表光速常数。当我们将 c 乘以 t 时，我们得到 ct，它的测量值为 1 光 m/c²。

在牛顿-伽利略图中，两个参考系 S 和 S’ 分别由坐标 （x， t） 和 （x’，t’） 给出，其中撇号符号，发音为 x 素数和 t 素数，用于区分两个相对参考系（并且不像在正常上下文中那样表示分化) .这些坐标系是可逆的，在伽利略相对论中，逆坐标系彼此等价。根据 S 的参考系，S’ 的坐标、位置和时间分别由 x’ = （x-vt） 和 t’ = （t- vx/c²） 给出。同样，从 S’ 的参考系来看，S 的坐标由 x = （x’ + vt’） 和 t = （t+vx/c²） 给出。然而，这些转换最终使光成为相对的，而不是时空的。问题来了，我们如何才能从 S →S’ 进行翻译，从而守恒 c（光速），同时按比例缩放时间和距离变量（更准确地说，时空连续体）？

推导这些翻译的一种方法是利用我们上面介绍的时空图，其中我们将时间按常数 c 缩放≈ 299 x 10⁸。我们正在寻找的翻译表示如下：

事实上，我们将利用参考系之间的这种对称性或等价性来推导出伽马因子作为相对参考系之间时空平移的公共比例因子，从而使它们反映出发光恒定性。这种相对运动的伽利略对称性由下图说明，该图表示我们引入的两个参考系是彼此的反比：

参考系之间的可逆对称性。图片由作者提供。
由于光速在所有参考系中都是恒定的，因此如果我们从两个参考系的原点开始（x = 0 和 t=0），光的路径将满足以下方程（回想一下，45⁰ 处的对角线代表光速，其中一个时间单位对应于一个单位距离内行进的距离）：

从 x 到 x’ 的转换由下面的等式给出，其中 x’ 只是 x 与速度和时间的乘积之间的差。现在，为了推导洛伦兹变换，我们需要一些因子γ来缩放我们的时空变换。β因子等于 v/c（速度和光速之比），用于缩放 ct（光速缩放时间）。如果我们扩展表达式，我们发现它在代数上简化为括号中的牛顿变换。正如我们将看到的，当洛伦兹因子 γ 趋近于 1 时，洛伦兹变换变得等同于它们的牛顿变换，这对应于我们日常的事件同时性概念。下面的公式演示了我们如何从初始公式到相对位置的伽马缩放变换公式：

同样，我们可以使用下面的等式推导出从 t 帧到 t’ 的时间转换。由于我们使用的是时空图，因此我们从 ct’ 开始。我们看到 ct’ 可以通过 ct 和 beta 之间的差值来计算，β缩放为 x，并且整个表达式由洛伦兹因子 γ缩放。我们可以通过扩展表达式来代数求解 t’，该表达式将 t’ 的解简化为 t-vx/c² 按 γ缩放：

当速度非常小时，vx/c² 减小到 0，γ 减小到 1，产生 t’=t。这个结果对应于我们日常的牛顿经验，即我静止时的 1 秒或多或少等于你的秒，同时相对于我以恒定的速度移动。

您可能已经注意到，向 x’ 的转换涉及 ct 作为项，而向 t’ 的转换涉及 x 作为项。通过在彼此的参考系转换中将项作为项进行分解，时间和空间交织成一个相互依赖的连续体，其中一个变量的单位变化对应于另一个变量中的单位变化。这种相互关系将解释洛伦兹变换所描述的时间膨胀和空间收缩的比例。

我们如何确定洛伦兹因子的值？一种方法是将我们的平移方程相乘并求解公因数。请记住，由于我们之前介绍的相等性，我们可以分别用 ct 和 ct’ 替换 x 和 x’。这将让我们抵消类似术语并解决γ：

现在我们可以通过以下 γ 替换来表示 x’ 参考系：

并且可以通过以下代入来表示 t’ 参考系：

在每个方程中，当速度 v 接近光速时，v²/c² 接近数字 1，分母的值接近 √0。我们从 E=mc² 知道，作为物理原理问题，具有静止质量的物体不能被加速到相等的流明速度。因此，分母的值在物理上不可能等于 0。0 限制表示无限快速度（表示变换的角度）。当速度接近无限时，时间接近静止，长度的测量接近于零。

另一方面，当速度较小时，v²/c² 是一个非常小的数字，分母的值接近 1。当分母（称为洛伦兹因子）等于 1 或 ~ 1 时，洛伦兹因子变得微不足道，方程近似于牛顿运动。也就是说，运动方程由分子给出，分子简化为牛顿运动方程。

洛伦兹因子是理解洛伦兹变换的关键。如果你回想起伽利略相对论，惯性参考系的可互换性是通过旋转来实现的。旋转由三角函数描述。三角函数守恒欧几里得距离。具体来说，旋转守恒半径。这意味着长度单位在转换过程中保持不变。

类似地，洛伦兹变换守恒时空度量。与欧几里得度量不同，时空度量将相对于光速的所有时空变换作为绝对值。出于这个原因，光速形成了一个渐近线，洛伦兹变换接近但不能相等。在时空图中，光速由等式 x = ct 和 x’ = ct’ 表示。如果你回想一下我们的时空图，渐近线由横跨两个轴的对角线组成。由于时空变换的范围都是无限的（这意味着它们输出的范围为 ˗ ∞ 到 + ∞），但对我们的对角线是渐近的，因此它们由双曲函数或旋转来描述。双曲旋转是类似于三角函数的函数，但使用双曲线而不是圆。与有限的圆不同，双曲旋转可以延伸到无限范围。它们与三角函数的等价物可以描述为对特殊数 e （2.718） 的指数运算，其中 sin（x） 的类似物用 sinh（x） 表示，与 cos（x） 的类似物用 cosh（x） 表示，分别由以下函数描述：

就像在单位圆 （sin x， cos x） 中描述它的点一样，（cosh x， sinh x） 形成单位双曲线的右半部分。在狭义相对论的背景下，双曲旋转的角度称为速度，用符号 eta η 表示。以下是等效于我们之前推导的洛伦兹变换的双曲旋转：

洛伦兹因子 γ 与双曲旋转速度之间的关系如下：

如果伽利略旋转守恒半径或欧几里得距离，那么洛伦兹变换守恒什么？它们守恒 Minkowski 度量，由以下等式给出，类似于欧几里得距离：

由于实际的洛伦兹变换发生在四个维度中，即 1 个时间维度和 4 个空间维度，或者类似地发生在 4 个时空维度，因此四维闵可夫斯基区间由以下方程给出：

下面的 gif 图将这些双曲变换可视化为二维时空扭曲，当速度接近光速时，这些时空扭曲接近对角线渐近线。网格上的扭曲表示由于观察者的相对速度而导致的时空度量扭曲。当速度接近光速极限时，空间（水平轴双曲线）收缩，时间（垂直轴双曲线）膨胀。这些交织在一起的变换守恒了闵可夫斯基度量 s²，该度量 s² 根据光速的不变性按比例缩放这些变换。

空间收缩和时间膨胀可以在静止的观察者和以匀速或惯性速度移动的观察者之间反转。如果你相对于静止的人均匀地以接近光速极限的运动，那么将你描述为静止而另一个人以接近光速移动同样是正确的。

五、度量张量：曲面的几何形状

狭义相对论中的洛伦兹变换发生在平坦空间伪欧几里得空间中。什么是平坦的空间？它是一种几何图形，其中度量或点之间的距离测量值是恒定的。最著名的平面空间度量是由勾股定理定义的。另一个平坦的度量包括我们上面讨论的 Minkowski 时空度量。

欧几里得度量将两点之间的距离定义为直角三角形最短边的平方长度之和的平方根。这源于勾股定理：a² + b² = c²。

从几何学上描述，两点之间的欧几里得距离由每个坐标 （x，y） 之间的平方差之和的平方根给出。

欧几里得距离作为向量的大小。
勾股定理可以推广到 n 个维度：

n 维中的欧几里得距离。
因此，我们可以通过下面的公式在三维空间中表示欧几里得距离：

六、三维欧几里得距离。

然而，这种概括将距离守恒为欧几里得平面空间的一个属性。换句话说，指标保持不变。

为了理解度量张量，我们需要学会将勾股定理视为平坦空间或欧几里得空间的特例。

换句话说，我们需要定义一个值中立空间，以便由勾股定理定义的欧几里得距离可以作为特例推导。

在我们这样做之前，我们必须问为什么在勾股定理中坐标之间的差是平方的？这可以用多种方式来解释，但直观的解释是几何的。它们是平方的，因为它产生长度相等的几何面积，因为面积是长度和宽度的乘积，这使我们能够将斜边计算为直角边的平方和的平方根。这个答案是由 Kronecker delta 定义的度量张量给出的，如果 i=j，则输出 1，如果 i≠j，则输出 0。

然而，我们也可以通过空间的广义度量来证明结果，其中度量张量由切线空间上平滑变化的内积组成。

什么是切线空间？切空间是与流形上的点相切的所有向量的集合。

方程的一般形式如下，其中 g 表示度量张量，μv 表示每个坐标项每个度量张量值的指数，dX 表示每个坐标的无穷小位移：

给定上述等式，我们可以将二维中两点之间的平方距离表示为以下总和：

由度量张量推广的两点之间的平方距离。
在上面的公式中，g 系数旁边的 0 和 1 以及 x 变量表示指数。具体来说，它们表示 0 和 1 的排列矩阵，即：01、00、11、10。

dx⁰ 和 dx¹ 系数表示两个不同坐标的无穷小位移，其中 0 和 1 是索引。将每个坐标的位移乘积乘以相应的值 g，即度量张量。

因此，在上述公式中，g表示每个指标的度量张量系数。为什么上面的公式中有四个项？因为两个点由四个坐标或标量值描述。在欧几里得几何中，隐式基向量是切向量 （0,1） 和 （1,0）。这些切向量跨越了整个欧几里得空间。现在 g 定义了向量空间上任何一点的切向量之间的内积。g 的值是通过基向量的所有可能组合的内积获得的。

当系数的值表示两点之间的正交关系时，g 的值简化为单位矩阵：

当三角形的角度垂直时，度量张量的系数，定义了平坦的欧几里得空间。

您可以将度量张量系数视为对应于置换矩阵的索引。
在二维或两个坐标的系统中，我们可以将欧几里得距离表示为度量张量与每个坐标之间距离的平方向量的乘积。因为对于平坦欧几里得空间中的直角，度量张量是一个单位矩阵，所以两点之间的平方距离减少到勾股定理，如下所示：

上述公式也可以表示为我们第一个公式中表示的线性加权组合：

欧几里得距离作为具有 g 值的线性加权和。
如上图所示，当 g=0 时，我们去掉后两项，将方程简化为欧几里得距离。因此，我们已经解释了度量张量的广义形式如何暗示欧几里得距离是一种特殊或限制情况。

当最短距离不能用欧几里得距离表示时怎么办？在我们的日常直觉中，我们预设相反线和相邻线的长度存在直角，以满足勾股定理作为斜边的距离度量。在线性代数中，它等同于假设正交基数作为空间的度量。基定义为跨越该向量空间的线性独立向量集。正交基数是垂直的单位向量或内积为零的单位向量。

但这种先验的假设在经验上可能是没有根据的。事实上，底层几何图形可能以不同的方式弯曲或倾斜。如果是这样的话，我们该如何表示两点之间的最短距离呢？为了定义非欧几里得空间，我们为我们的度量选择不同的基向量。这些基向量的置换空间的内积将通过两点的任何无穷小位移的线性组合输出定义该度量中距离和角度的度量张量，由公式给出：

广义 Rhiemannian 距离。
现在，让我们看一个极坐标 （r， θ） 的例子，其中 r 表示半径，θ θ 表示角度。g 度量张量是通过 （r， θ） 的置换空间的内积得到的，如下图所示：

极坐标的度量张量。
如果我们考虑欧几里得极坐标，度量张量将出现在下面的矩阵中：

极坐标的度量张量的特定实例化。
这是因为距离是通过以下方式计算的：

现在，两点之间的距离 （r¹θ¹） 和 （r²θ²） 是通过计算距离 r²-r¹ 和 θ²-θ¹ 并将它们代入以下公式来给出的：

到目前为止，我们所有的示例都在二维空间中。当然，我们可以将同样的想法扩展到三维或N维空间。三维空间的度量张量将是一个 3x3 矩阵，依此类推。

理解度量张量是理解广义相对论和爱因斯坦场方程的主要垫脚石。

在广义相对论中，爱因斯坦的场方程利用度量张量来描述时空的弯曲几何。

具体来说，爱因斯坦的场方程使用了三个张量：1）爱因斯坦的张量G，它描述了度量张量导数的时空曲率，2）能量-应力张量T，它描述了宇宙中物质和能量的分布，以及3）度量张量g，它定义了弯曲几何中长度和角度的度量。爱因斯坦的场方程通常用以下等式来概括：

在广义相对论中，度量张量由一个 4x4 矩阵组成，该矩阵由 16 个分量组成。就像在我们的二维示例中一样，度量张量由所有维度的排列空间组成，在本例中，空间的 3 个和时间的 1 个组合成 4 个时空维度。但是，由于矩阵必然是对称的，因此这些分量中只有 10 个是相互独立的。

度量张量的通用形式如下所示：

度量张量的值随着时空的曲率而变化，因为它们编码了质能分布。因此，与在所有变换中守恒长度的欧几里得距离不同，曲几何则不然。这就是为什么度量张量是理解广义相对论的一个重要方面。

既然你已经研究了这些概念，那么你可能会对物理学中的复杂思想和数学形式主义者感到畏惧！