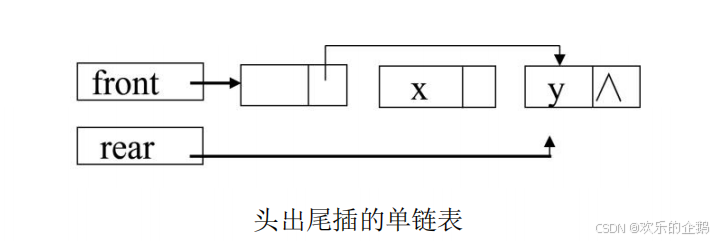
在halcon中，区域R是用一系列行程（run）的集合表示的，run的形式为（Row，ColumnBegin，ColumnEnd），分别对应行坐标、列开始坐标、列结束坐标，这种保存区域的方法被称作行程表示法或行程编码。因为图像数据是按行保存的，所以使用水平行程，行程  在R内的存储顺序定义为：  。用行程编码法可以减少存储空间，避免区域外像素的检查，还可以显著提升算法的速度。

一个区域的行程编码

        形态学的处理需要涉及两个区域，一个是想处理的区域，用R表示，一个是能够描述感兴趣形状的区域，也被称作结构元，用S表示，结构元有时需要指定参考点。在halcon中膨胀被定义为取出S中的每个点s，根据s所对应的向量来平移R，然后对全部平移得到的区域取并集。假设我们使用一个3×3的矩形结构元，参考点为矩形中心，如下图，红色圆圈所在位置为参考点，结构元一共有9个元素，意味着需要8次平移，剩下的一次对应原区域R(平移向量=0向量)，实际处理中，我们可以将R向上平移一次、向下平移一次加上R得到三个区域，再将三个区域分别向左和向右平移，由于行程编码是水平的，对行程的左右移动只需要将行程的列开始坐标减去最大平移量、列结束坐标加上最大平移量即可实现，这可以极大的提升算法速度。

3×3矩形结构元

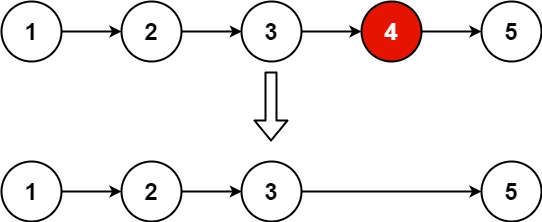
        halcon中的腐蚀被定义为将结构元S在平面内移动，如果S被完全包含在R中，就将其参考点所在位置加入到输出结果中。即结构元S在R中“逛荡”，每“逛荡”一下，就记下S参考点的位置，直到“逛荡”完所有位置。从上面的定义不难看出，腐蚀不仅可以收缩区域，将彼此相连的物体分开，还可以实现类似模板匹配的功能。下图展示了膨胀和腐蚀的过程，膨胀使用矩形结构元，腐蚀使用十字结构元，腐蚀的结果只有两个像素，它们正是完全匹配十字的位置。膨胀和腐蚀还有一个有趣的属性，在进行补集操作时，它们彼此之间是互为对偶的，对前景的一个膨胀处理等同于对背景的一个腐蚀处理，对前景的一个腐蚀处理等同于对背景的一个膨胀处理，所以膨胀和腐蚀只需要实现其中的一个就可以了，另一个通过对偶性即可得到。

膨胀

腐蚀

        连通区域是一组像素点的集合，集合中所有点都彼此连通。两个像素的连通性有两种定义：

        4连通：一个像素在另一个像素的上方，下方，左侧或右侧。

        8连通：一个像素在另一个像素的上方，下方，左侧，右侧，左上方，左下方，右上方或右下方。

        连通区域分析是指将一个区域分割为彼此互相独立的连通区域，在halcon中由connection算子实现。

        需要注意的是，对前景和背景要使用不同的连通性定义。如果8连通描述前景、则4连通描述背景，如果4连通描述前景、则8连通描述背景。

        由于区域由行程编码表示，连通区域的计算相对简单，按从上到下顺序扫描每一行，按从左到右顺序扫描当前行所有run，将当前run与上一行的run进行比较，如果与上一行的run都不连通，标记为新的区域，如果当前run未标记并与上一行的某个run连通，则将当前run标记为与连通run相同的label，否则将两个run的label进行合并。算法的开始需要声明一个树结构（一维数组），在合并两个run时，寻找label的根部，插入等价关系，直至整个算法结束。具体的计算过程请看下图，图中的白色区域即为要计算的区域，一共有11个run，分别在它们的左上角用红色记号标出，从第一个run所在的行开始扫描，由于上一行没有任何run，当前行的4个run被分别标记为1，2，3，4（洋红色标出），继续扫描下一行，从第五个run开始，第五个run与第一个run连通，所以标记为1，继续下一个run（第六个），第六个run先与第二个run连通，首先标记为2，而后又与第三个run连接，由于已经被标记过，所以需要合并，此时2小于3，添加关系2<-3（3指向2），并将第三个run的标记改为2，继续下一个run（第七个）,与第三个run连接（注意，此时第三个run的label已修改为2），标记为2，继续下一个run，第八个run标记为4，继续扫描下一行，第九个run标记为1，第十个run先与第七个run连接，标记为2，后与第八个run连接，需要合并，添加关系2<-4，修改第八个run的label为2，扫描最后一行，第十一个run先与第九个run连接，标记为1，后与第十个run连接，所以要合并，添加关系1<-2，修改第十个run的label为1。此时区域内的所有像素都被标记好了，同时我们还有（2<-3）(2<-4)（1<-2）这样的对应关系，不难得到这个区域实际是一个独立的区域。

连通区域分析示意图

        有了上面的知识之后，实现halcon中的fill_up（填充区域内的孔洞）就不难了，我们看下面的图，红色区域R为二值化所得，我们的目标是对R进行孔洞填充。很自然的，R的孔洞必然在R的补集中，所以求出R的最小外接矩形Rect（平行于坐标轴），用Rect减去R就得到了R的补集R’，由于孔洞是彼此独立的，这时对R’进行连通区域分析，得到很多个区域{R1,R2,R3,R4..……}，显然并不是每个区域都是孔洞，那怎么判断呢？也很简单，只要这个区域与Rect连通，那这个区域就不是孔洞，怎么判断与Rect是否连通呢？直接用两个区域的外接矩形是否有重合的边就够了，是不是很简单？有一点需要注意的是，在计算R’的连通区域时，应该使用4连通。

目标区域

R补集的连通区域计算

填充之后的区域

        目前connection、fill_up已经加入到测试demo中，connection会同时计算区域的area、row1、column1、row2、column2、circularity、ra、rb、phi、rect2_phi、rect2_len1、rect2_len2等属性，性能接近halcon，欢迎大家测试。

connection

fill_up