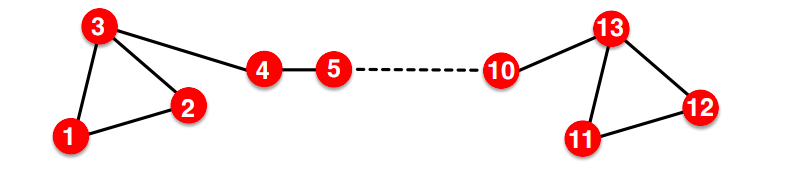
最小生成树
Prim算法
从某一顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,知道所有顶点都纳入为止。

时间复杂度O(|V|^2)
适合用于边稠密图
实现思想

从V0开始,总共需要n-1轮处理
每一轮处理:循环遍历所有结点,找到lowCast最低的,且还没加入树的顶点。
再次循环遍历,更新还没加入的各个顶点的lowCast的值(每一轮时间复杂度O(2n))
Kruskal算法
每次选择一条权值最小的变,使这条边的两头联通(原本已经联通的就不选),知道所有结点都联通。

时间复杂度O(|E|log2|E|)
适合用于边稀疏而顶点较多的图
实现思想
初始:将各条边按权值排序
共执行e轮,每轮判断两个顶点是否属于同一集合,需要O(long2e)
最短路径
单源最短路径
BFS算法(无权图)
就是对BFS的小修改,在visit一个顶点时,修改其最短路径长度d[]并在path[]记录前驱结点
Dijkstra算法(带权图、无权图)
final[ ]:标记各顶点是否已找到最短路径
dist[ ]:最短路径长度
path[ ]:路径上的前驱
时间复杂度:O(n^2)即O(|V|^2)
👩💻 Dijkstra算法并不适合于有负权值的带权图
各顶点间的最短路径
Floyd算法(带权图、无权图)
求出每一对顶点之间的最短路径。
使用动态规划思想,将问题的求解分为多个阶段。
//……准备工作,根据图的信息初始化矩阵A和path
for(int k = 0;k < n;k++){ //考虑以vk作为中转点
for(int i = 0;i < n;i++){ //遍历整个矩阵,i为行号,j为列号
for(int j = 0;j < n;j++){
if(A[i][j] > A[i][k] + A[k][j]){ //以vk为中转点的路径更短
A[i][j] = A[i][k] + A[k][j]; //更新最短路径长度
path[i][j] = k; //中转点
}
}
}
}时间复杂度O(|V|^3) ; 空间复杂度O(|V|^2)
👩💻 Floyd算法可以用于负权值带权图
👩💻 Floyd算法不能解决带有“负权回路”的图,这种图有可能没有最短路径
| BFS算法 | Dijkstra算法 | Floyd算法 | |
|---|---|---|---|
| 无权图 | ✔️ | ✔️ | ✔️ |
| 带权图 | ❌ | ✔️ | ✔️ |
| 带负权值的图 | ❌ | ❌ | ✔️ |
| 带负权回路的图 | ❌ | ❌ | ❌ |
| 时间复杂度 | O(|V|^2)或O(|V|+|E|) | O(|V|^2) | O(|V|^3) |
| 通常用于 | 求无权图的单源最短路径 | 求带权图的单源最短路径 | 求带权图中各顶点间的最短路径 |
🐧 也可以用Dijkstra算法求所有顶点间的最短路径,重复|V|次即可,总的时间复杂度也是O(|V|^3)
有向无环图描述表达式
定义:一个有向图中不存在环。(DAG图)
DAG描述表达式
【2019统考真题】用有向无环图描述表达式(x+y)((x+y)/x),需要的顶点个数至少是(A)
A.5 B.6 C.8 D.9

在表达式的有向无环图表示中,不可能出现重复的操作数顶点。
解题步骤
- 把各个操作数不重复地排成一排
- 标出各个运算符的生效顺序(先后顺序有点出入无所谓)
- 按顺序加入运算符,注意“分层”
- 自底向上逐层检查同层的运算符是否可以合体
拓扑排序
- AOV网:用DAG图(有向无环图)表示一个工程。顶点表示活动,有向边<Vi,Vj>表示活动Vi必须先于活动Vj进行
- 每个AOV网都有一个或多个拓扑排序序列
- 采用邻接表:时间复杂度O(|V|+|E|);采用邻接矩阵:时间复杂度O(|V|^2)
- 用DFS实现拓扑排序
拓扑排序的实现
- 从AOV网中选择一个没有前驱(入度为0)的顶点并输出
- 从网中删除改顶点和所有以它为起点的有向边
- 重复1和2直到当前的AOV网为空或当前网中不存在无前驱的顶点为止(说明有回路)
逆拓扑排序
- 从AOV网中选择一个没有后继(出度为0)的顶点并输出
- 从网中删除改顶点和所有以它为起点的有向边
- 重复1和2直到当前的AOV网为空
关键路径
- AOE网:在带权有向图中,以顶点表示事件,以有向边表示活动,以边上的权值表示完成该活动的开销。
- 仅有一个入度为0的顶点,称为开始顶点(源点)
- 仅有一个出度为0的顶点,称为结束顶点(汇点)
- 具有最大路径长度的路径称为关键路径,而把关键路径上的活动称为关键活动
求关键路径的步骤
- 事件Vk的最早发生时间ve(k)——决定了所有从Vk开始的活动能够开工的最早时间
- 按拓扑排序序列,依次求各个顶点的ve(k):
- ve(源点) = 0
- ve(k) = Max{ve(j) + Weight(vj,vk)},vj为vk的任意前驱
- 按拓扑排序序列,依次求各个顶点的ve(k):
- 事件Vk的最迟发生时间vl(k)——它是指在不推迟整个工程完成的前提下,该事件最迟必须发生的时间。
- 按逆拓扑排序序列,依次求各个顶点的vl(k):
- vl(汇点) = ve(汇点)
- vl(k) = Min{vl(j) - Weight(vk,vj)},vj为vk的任意后继
- 按逆拓扑排序序列,依次求各个顶点的vl(k):
- 活动Ai的最早发生时间e(i)——指该活动弧的起点所表示的事件的最早发生时间
- 若边<vk,vj>表示活动Ai,则有e(i) = ve(k)
- 活动Ai的最迟发生时间l(i)——它是指该活动弧的重点所表示事件的最迟发生事件与该活动所需时间之差。
- 若边<vk,vj>表示活动Ai,则有l(i) = vl(j) - Weight(vk,vj)
- 活动Ai的时间余量d(i)=l(i)-e(i)。d(i)=0的活动Ai是关键活动。
- d(i) = l(i) - e(i)
特性
- 若关键活动耗时增加,则整个工程的工期将增长
- 缩短关键活动的时间,可以缩短整个工程的工期
- 当缩短到一定程度时,关键活动可能编程非关键活动
- 可能有多条关键路径,只提高一条关键路径上的关键活动速度并不能缩短整个工程的工期,只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的。