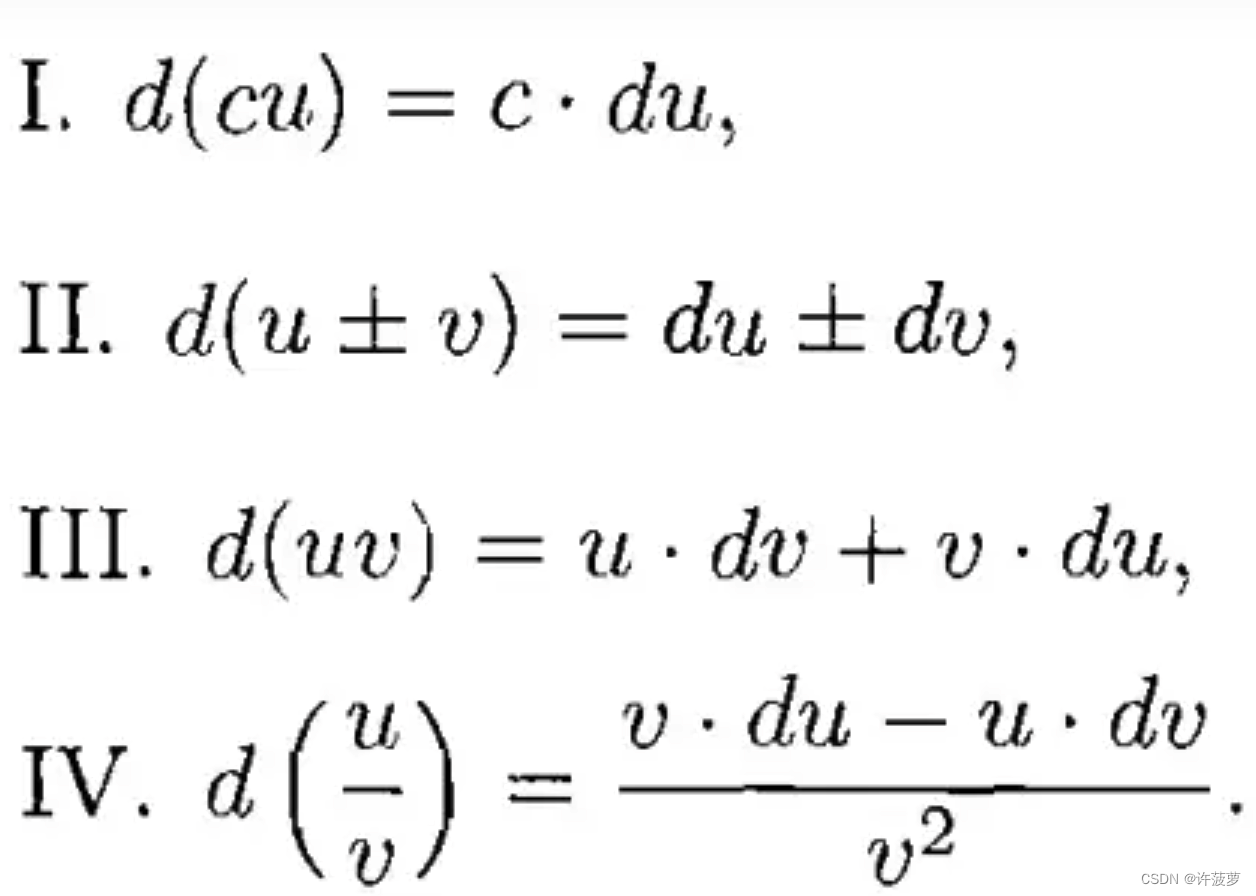知乎:坐标系转换
1.Frenet 坐标系
什么是 Frenet 坐标系:
为什么使用 Frenet 坐标系: 通常情况,我们只会关注车辆当前距离左右车道线的距离,来判断是否偏离车道,是否需要打方向盘进行方向微调。而不是基于汽车的出发点,那样就太远了
往往道路是弯曲的,在直角坐标系下要计算出车辆行驶的距离要考虑道路曲率会非常麻烦。而在Frenet坐标系中,原点所在参考线与车道中心线平行,容易确定车辆偏离车道中心线的距离以及车辆沿车道中心线的行驶距离。因此使用Frenet坐标系可以忽略道路曲率的影响,让道路表达更加直观、简洁。
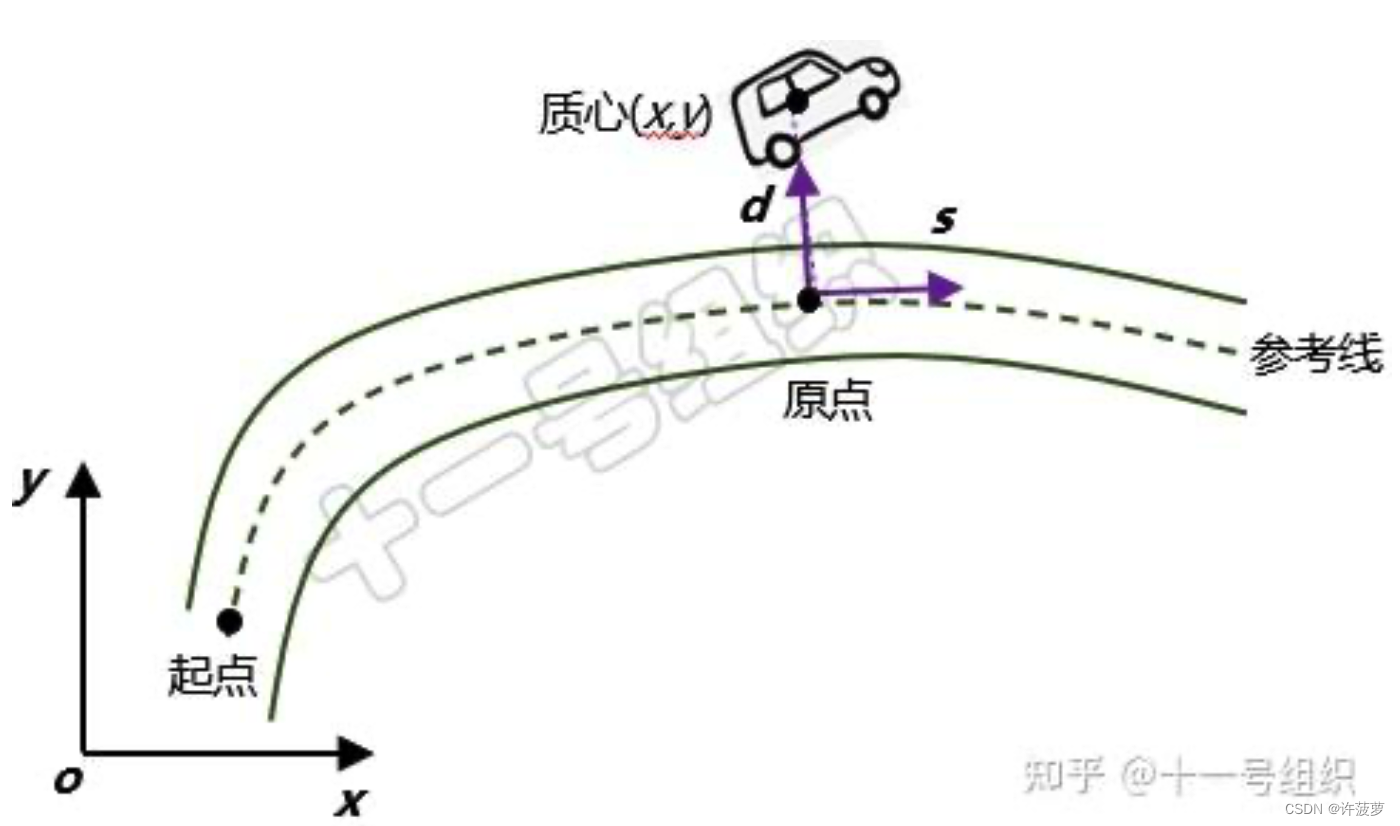


Frenet 坐标系相当于把道路抻直了
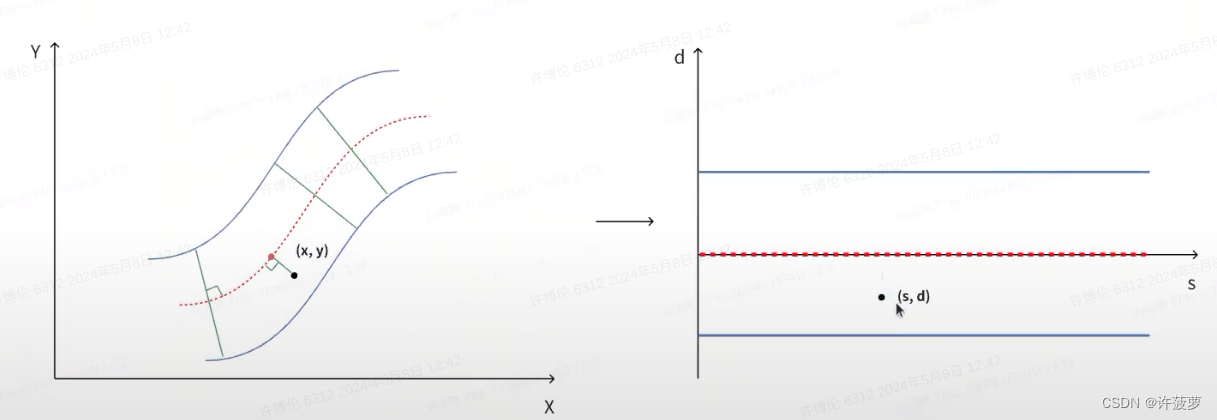
2.笛卡尔坐标系
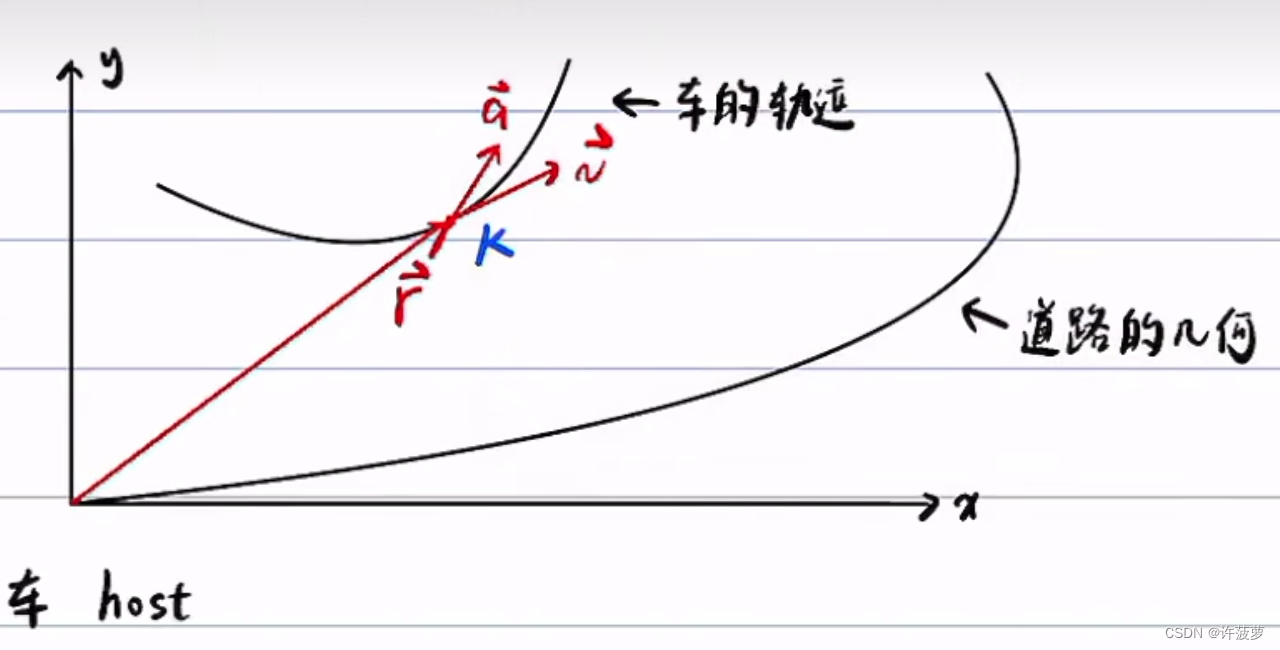

3.两者转换
在实践中只需要记住结论
推导博客
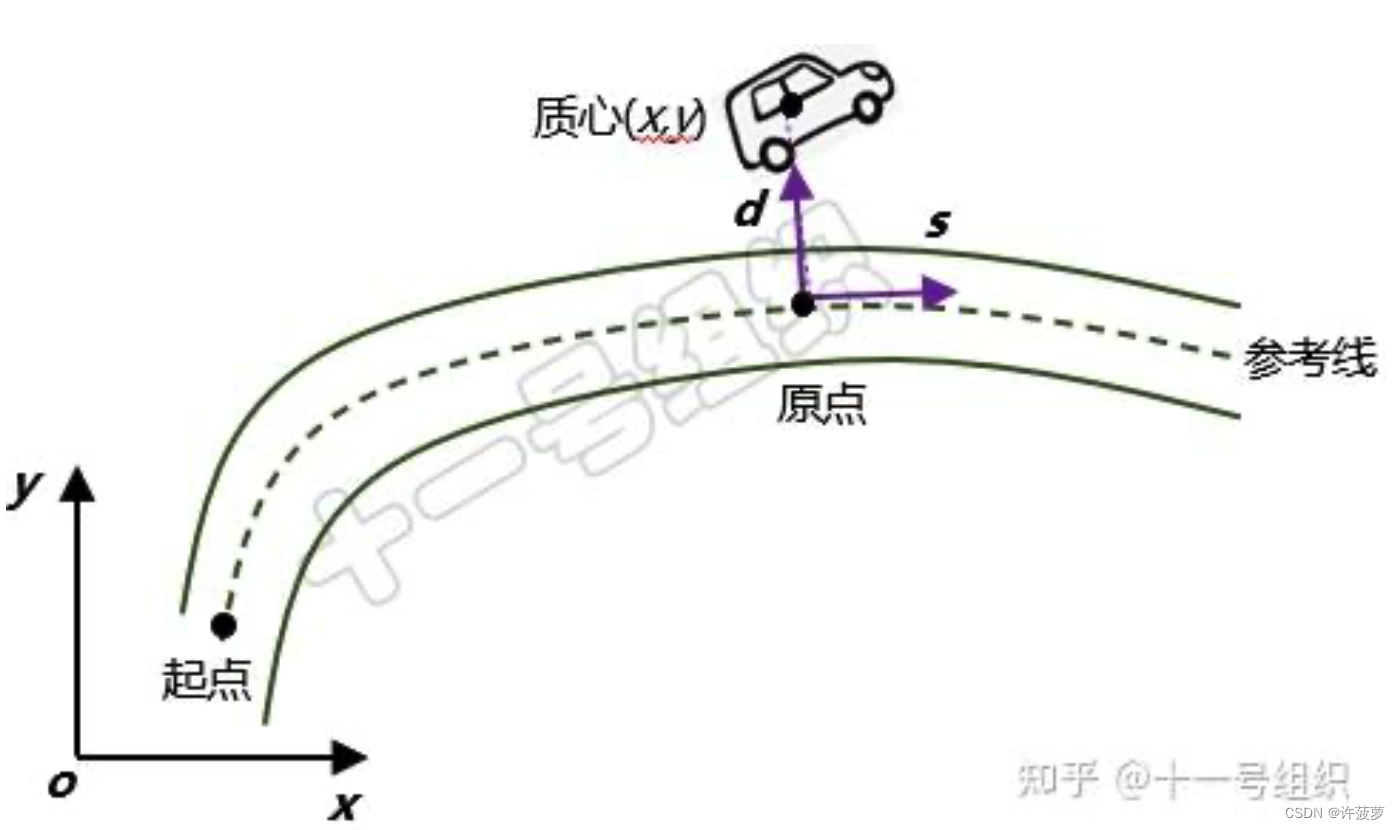
某一时刻,假设车辆质心在全局笛卡尔坐标系下的坐标为(x,y)
**原点:**车辆质心到参考线上的投影点称为
原点切线方向称为s轴方向或纵轴方向
原点法线方向称为d轴方向或横轴方向
s:值指的是参考线上的原点与起点之间曲线的长度,也就是车辆在道路上的纵向行驶距离。
d:值指的是原点与车辆质心之间的距离,也就是车辆偏离道路中心线的距离。
车辆质心随着时间在不断变化,因此Frenet坐标系的原点也在不断变换,所以Frenet坐标系是一个移动坐标系。
4.存在的问题
输入的坐标往往是笛卡尔坐标,在中间预测轨迹时使用 Frenet 坐标,最后输出给下游时还要转换成笛卡尔坐标,所以需要将 Frenet 和笛卡尔坐标之间相互转换,但是将 Frenet 坐标转为笛卡尔坐标会有以下问题

5.参考线生成
如果 Frenet 坐标建立的不够精确就会导致问题越明显,所以参考线的生成要满足一下约束,最终效果生成一条平滑的曲线 :
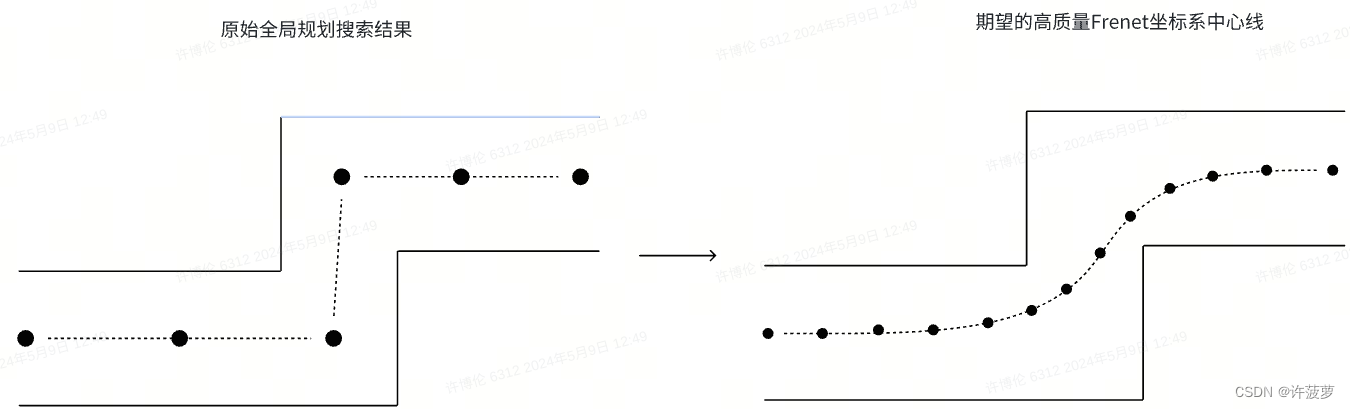
S1 :插值扩充点的个数
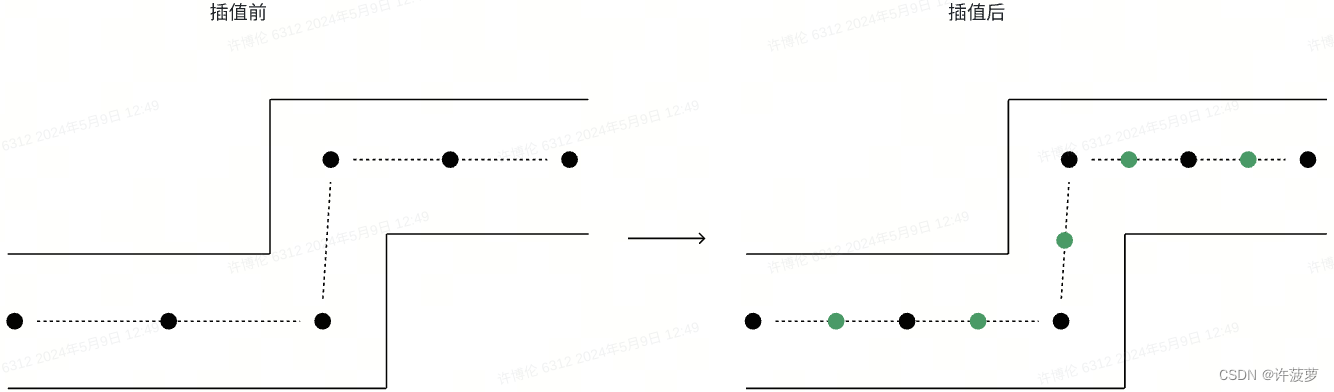
S2:将点与点之间变得平滑
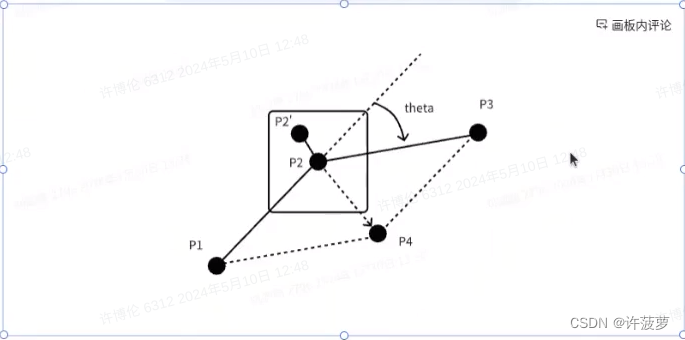
a. 考虑为了使连接成的轨迹尽可能满足平滑的要求,参考线之间应该又怎样的性质?
-
- 直线平滑度最高,自车行驶也最容易;对应图中theta越小、|P2P4|越小则越接近直线,如果 thete 很大就会是一条直线
-
- 行驶距离越短越好,所以相邻两点距离和应该越小越好 m i n ∑ ∣ ∣ P k P k − 1 ∣ ∣ 2 min\sum ||P_{k}P_{k - 1}||_{2} min∑∣∣PkPk−1∣∣2
-
- 点间距越均匀越好 m i n { a b s ( ∣ ∣ P k + 1 P k ∣ ∣ 2 − ∣ ∣ P k P k − 1 ∣ ∣ 2 ) } min\left \{ {abs(||P_{k+1}P_{k}||_{2} - ||P_{k}P_{k-1}||_{2})} \right \} min{abs(∣∣Pk+1Pk∣∣2−∣∣PkPk−1∣∣2)}
-
- 为了避免调整位置前后轨迹变化太大,应该限制每个点可以偏移原始点的位置,
同时最小化偏移距离 m i n ∑ ∣ ∣ P k P k ′ ∣ ∣ 2 min\sum ||P_{k}P_{k}{'}||_{2} min∑∣∣PkPk′∣∣2
- 为了避免调整位置前后轨迹变化太大,应该限制每个点可以偏移原始点的位置,
b. 把这个问题用数学表达式写出来:考虑上面提到的性质,把不满足上述性质的程度记作J,根据上面的描述,J应该包含下面几项,注意式中都对距离取了平方,取平方可以提升计算效率
1. 平滑代价:
∑
∣
∣
2
P
k
−
P
k
−
1
−
P
k
+
1
∣
∣
2
2
\sum ||2P_{k} - P_{k - 1} - P_{k + 1}||_{2}^{2}
∑∣∣2Pk−Pk−1−Pk+1∣∣22
2. 偏移代价:
∑
∣
∣
P
k
P
k
′
∣
∣
2
2
\sum ||P_{k}P_{k}{'}||_{2}^{2}
∑∣∣PkPk′∣∣22
3. 距离代价:
∑
∣
∣
P
k
P
k
−
1
∣
∣
2
2
\sum ||P_{k}P_{k - 1}||_{2}^{2}
∑∣∣PkPk−1∣∣22(此部分代价同时可以反应均匀性)
c. 每个点还应该满足位置限制条件,也就是将每个点限制在框中
1.
x
m
i
n
<
=
x
k
−
x
k
′
<
=
x
m
a
x
x_{min} <= x_{k} - x_{k}^{'} <= x_{max}
xmin<=xk−xk′<=xmax
2.
y
m
i
n
<
=
y
k
−
y
k
′
<
=
y
m
a
x
y_{min} <= y_{k} - y_{k}^{'} <= y_{max}
ymin<=yk−yk′<=ymax
d. 于是,我们想让参考点变得符合我们对中心线预期的问题,就变成了下面这样一个数学问题,在满足限制条件的情况下,使得J的值最小,其中w表示各个项目的重要程度;
1.
m
i
n
{
J
=
w
1
∑
∣
∣
2
P
k
−
P
k
−
1
−
P
k
+
1
∣
∣
2
2
+
w
2
∑
∣
∣
P
k
P
k
′
∣
∣
2
2
+
w
3
∑
∣
∣
P
k
P
k
−
1
∣
∣
2
2
}
min\left \{ J = w_{1}\sum ||2P_{k} - P_{k - 1} - P_{k + 1}||_{2}^{2} + w_{2}\sum ||P_{k}P_{k}{'}||_{2}^{2} + w_{3}\sum ||P_{k}P_{k - 1}||_{2}^{2} \right \}
min{J=w1∑∣∣2Pk−Pk−1−Pk+1∣∣22+w2∑∣∣PkPk′∣∣22+w3∑∣∣PkPk−1∣∣22}
2. s.t.
x
m
i
n
<
=
x
k
−
x
k
′
<
=
x
m
a
x
x_{min} <= x_{k} - x_{k}^{'} <= x_{max}
xmin<=xk−xk′<=xmax、
y
m
i
n
<
=
y
k
−
y
k
′
<
=
y
m
a
x
y_{min} <= y_{k} - y_{k}^{'} <= y_{max}
ymin<=yk−yk′<=ymax
e. 问题求解,这其实是一个标准的二次规划问题,调用OSQP这个运算库就可以求解出来结果
1. 二次规划问题:目标函数是凸二次函数(最高次数为2,且为凸函数),约束条件是线性函数
2. 二次规划问题的标准形式
m
i
n
1
2
x
T
H
x
+
q
T
x
s
.
t
.
a
T
x
=
b
h
T
x
<
=
t
\begin{array}{l} min\ \frac{1}{2} x^{T}Hx + q^{T}x \\ s.t.\ \ \ \ a^{T}x = b \\ \ h^{T}x <= t \end{array}
min 21xTHx+qTxs.t. aTx=b hTx<=t
上方是问题的形式,下方的问题的约束
6.Frnet 坐标转笛卡尔坐标
龙格现象:
虽然高次多项式会拟合出一条更精确的曲线,但是当次数变高是会出现震荡的现象,所以我们应该使用低次多项的方式拟合一条曲线

微分基本公式及法则