欢迎来到雲闪世界。从职业角度来说,我是个非常奇怪的人:我在一家初创公司担任软件/机器学习工程师,拥有物理学硕士学位,即将为航空航天和机械工程博士学位论文答辩。在我不断变化的职业生涯中,有两件事始终不变:我对科学的热爱和对编程的热情。
将科学与编码相结合的一种绝妙方法是进行建模。我的意思是,为了描述世界,您需要根据某种程度的现实近似做出合理的假设。基于此假设和您的起始近似,我们可以模拟给定的过程。模拟将为我们提供一些源自原始假设但在模拟之前无法准确预测的结果。
例如,假设我们想算出一个栅栏里能容纳多少头牛。物理学家会做出一个相当奇怪的假设:
“让我们想象一下一头方形的牛”
意思是,我们把牛的形状近似为正方形。然后我们把栅栏近似为一个更大的正方形(这个假设更合理)。
现在,让我们给问题加点盐,假设奶牛的长度是随机的,这意味着每头奶牛的正方形大小都是不一样的,每个正方形长度的分布是高斯分布的结果,平均值 = 2,方差 = 1。我们假设栅栏很大,L = 10。
为了解决这个问题,我们必须进行非常简单的蒙特卡罗模拟。我们不断在 10x10 的方形围栏内添加方形奶牛,看看我们是否遇到了问题,因为我们无法继续添加它们。我们重复这个过程 N=1000 次,并提取奶牛数量的平均值。
现在,很明显,这是一种计算围栏中可以容纳多少头牛的粗略方法,这实际上是物理学界的一个著名笑话。尽管如此,它完美地描述了建模的方法。
现在我喜欢人工智能。我每天都在研究和从事人工智能工作,从 2019 年开始我就一直这样做。不过,我确实不同意人工智能的一件事是,由于有了人工智能,我们不再需要建模了。我们可以训练一个机器学习模型。
这是错误的(也有点可悲)。我们需要建模,因为建模是理解我们周围世界的基础。
希望通过一些方形的奶牛和同情心,我能说服你,建模很酷。
在这篇博文中,我将使用一种非常强大的建模工具,即马尔可夫链,来模拟个人的职业 发展。我们将从刚毕业的人开始,并对他们未来将做什么给出一些概率假设。通过将这些假设代入马尔可夫链模型,我们将得到个人职业结果的分布。让我们开始吧!
0. 马尔可夫链介绍
如果你们中的一些人已经阅读了我的一些文章(谢谢,我爱你,你是最棒的❤),你们已经知道我喜欢马尔可夫链。如果你熟悉马尔可夫链,你可以放心地跳过这部分。
如果您不熟悉马尔可夫链,在本文中,我将概括地讨论它们,并且以我的拙见,对于以前从未听说过马尔可夫链并想了解其要点的人来说,这是一个很好的指南。
说实话,我们不需要为这篇博文了解很多马尔可夫链,因为它的代码量很大,但理论量不大,所以我只会非常快速地描述它的工作原理。为简洁起见,我将以职业发展为例来准确描述这一点。
让我们考虑一个随机事件E。此事件可能发生在时间 t=0、t=1、t=n。在每个时间(1 到 n),事件可以假设不同的值。例如,在 t=2(即 2 年)之后,该人可能正在攻读学士学位。我们用数学表达式将其写成:
![]()
图片来自作者
现在,假设某人在第 2 年攻读学士学位,那么 5 年后该人仍在学习的概率是多少?马尔可夫链假设告诉我们,为了知道这一点,只需要知道前一年发生了什么,例如以下表达式:
![]()
告诉我们,如果一个人在第一年攻读学士学位,那么他们继续攻读学士学位的可能性会相当高(0.8)。
我们可以在第 3、4、5 年后做同样的事情,只需考虑第 2、3 和 4 年发生的事件。因此,我们称之为链。
现在,这并不是特别有趣,但我们可以问自己:10 年后这个人就业的概率是多少?这将是在时间 t=10 时所有其他事件(拥有学士学位的人、拥有硕士学位的人、没有学士学位的人等)的总和(加起来)。
这将是我们模拟的核心。
1. 我们的模拟假设
为了这个案例研究,我创建了一个可能的职业选择列表,考虑到刚高中毕业的人的起点。
此人可以:
- 根本不要上大学
- 去上大学
如果他们上大学,他们可以:
- 去常春藤盟校学习,
- 去州立大学,
- 去一所社区大学。
对于每个人来说,他们可以前往:
- 干
- 商业
- 人文
之后,他们可以选择实习,也可以不实习。无论如何,之后,他们可以选择就业或失业。这是路径,看起来是这样的:
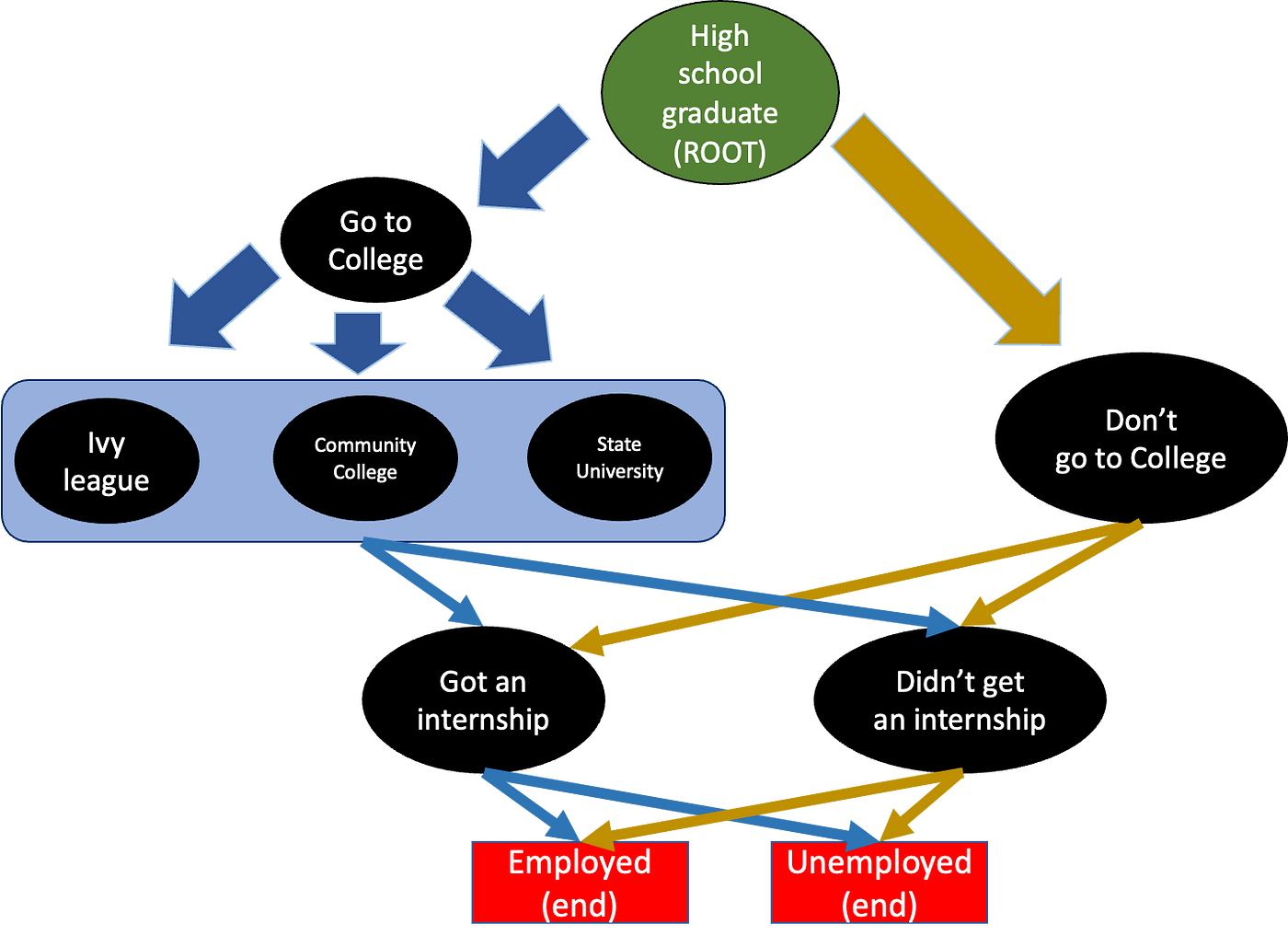
图片由作者制作
现在,每个黑色圆圈(以及最后的红色方块)都配备了一个概率级别,即在给定前一个状态的情况下,我们到达给定状态的概率。例如,常春藤联盟可能配备概率 = 0.2,这意味着,假设我们上过大学(前一个节点),我们也将去常春藤联盟大学。在图中,为了简洁起见,我省略了学习专业(人道主义、STEM 或商业)。
每个黑色圆圈还配有一个持续时间。“不上大学”的持续时间为 0,因为找工作/实习是一个即时的决定,而“常春藤盟校”的持续时间为 4。红色方块有一个“薪水”,就像在现实生活中一样,它会根据前一个节点而变化。例如,没有任何学位的人(平均而言)会比有实习经历的常春藤盟校学生赚得更少。当然,“失业”的薪水是 0。
重要提示!!!这些是我的模拟假设。您可以根据自己认为更符合您具体情况的假设随意更改它们。
现在,我们能用这些东西做什么?很多事情。但简而言之,我们可以在 Python 系统中运行模拟并分析响应。这就是所谓的蒙特卡洛方法。
2. 蒙特卡罗模拟
一切看起来都很好,但我们需要以数字形式获取数据,而不仅仅是文字。第一件事是找到模拟数据的格式。有很多方法可以做到这一点:定义二叉树、定义图形、定义表格……
为了简单起见,我将这些数据存储在 .json 文件中。我这样做是因为浏览 json 文件很简单,它会变成 Python 变量中的字典。
这是 .json 文件:
{
“HighSchoolGraduate” : {
“GoToCollege” : {
“概率” : 0.7 ,
“持续时间” : 0 ,
“IvyLeague” : {
“概率” : 0.1 ,
“持续时间” : 4 ,
“STEM” : {
“概率” : 0.4 ,
“WithInternship” : {
“概率” : 0.7 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.99 ,
“AvgSalary” : 120000
} ,
“失业” : {
“概率” : 0.01
}
} ,
“WithoutInternship” : {
“概率” : 0.3 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.9 ,
“平均薪资” : 110000
} ,
“失业” : {
“概率” : 0.1
}
}
} ,
“人文” : {
“概率” : 0.3 ,
“有实习” : {
“概率” : 0.7 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.97 ,
“平均薪资” : 90000
} ,
“失业” : {
“概率” : 0.03
}
} ,
“无实习” : {
“概率” : 0.3 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.85 ,
“平均薪资” :80000 } ,
“失业
” : {
“概率” : 0.15
}
,“商业” :{
“概率” : 0.3 ,
“有实习” : {
“概率” : 0.7 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.98 ,
“平均薪资” : 100000
} ,
“失业” : {
“概率” : 0.02
}
} ,
“无实习” : {
“概率” : 0.3 ,
“持续时间” : 0 ,
“就业” :{ “
概率” : 0.88 ,
“平均薪资” : 90000
} ,
“失业” : {
“概率” : 0.12
}
}
}
,“州立大学” :{ “概率” :0.5 ,“持续时间” :4 ,“STEM” :{ “概率” :0.4 ,“有实习” :{ “概率” :0.7 ,“持续时间” :0 ,“就业” :{ “概率” :0.97 ,“平均薪资” :80000 } ,“失业” :{ “概率” :0.03 } } ,“无实习” :{ “概率” :0.3 ,“持续时间” :0 ,“就业” :{ “概率” :0.9 ,“平均薪资” :70000 } ,“失业” :{ “概率” :0.1 } } ,“人文” :{ “概率” :0.3 ,“实习” :{ “概率” :0.7 ,“持续时间” :0 ,“就业” :{
“概率” : 0.95 ,
“平均薪资” : 60000
} ,
“失业” : {
“概率” : 0.05
}
} ,
“无实习” : {
“概率” : 0.3 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.85 ,
“平均薪资” : 50000
} ,
“失业” : {
“概率” : 0.15
}
}
} ,
“商业” : {
“概率” : 0.3 ,
“有实习” : {
“概率” : 0.7 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.96 ,
“平均薪水” : 75000
} ,
“失业” : {
“概率” : 0.04
}
} ,
“无实习” : {
“概率” : 0.3 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.87 ,
“平均薪水” : 65000
} ,
“失业” : {
“概率” : 0.13
}
}
}
} ,
“社区大学” : {
“概率” : 0.4 ,
“持续时间” : 2 ,
“就业” : {
“概率” : 0.92 ,
“平均薪水” : 50000
} ,
“失业” : {
“概率” : 0.08
}
}
} ,
“不去大学” : {
“概率” : 0.3 ,
“持续时间” : 0 ,
“就业” : {
“概率” : 0.85,
"平均薪资" : 35000
} ,
"失业" : {
"概率" : 0.15
}
}
}
}现在你可能会问……这些数字是从真实数据库中得到的吗?绝对不是。这些数字完全是任意的,你可以自己做研究/实验。在我的假设中,我确保路径的每个级别的概率总和为 1(这是强制性的),并且最长的教育时间对应于最长的平均工资,这意味着如果你待的时间更长,那么在就业时,平均而言你会赚更多的钱。
用你喜欢的名字保存此文件。我发挥了很大的创造力,选择了这个名字:
职业决策树.json
但你可以选择你喜欢的名字。别忘了它。🙂
我们模拟的目标是检索我在 JSON 文件中手动注入的以下考虑因素,以及您在现实生活中可以从统计数据中找到的考虑因素:
- 受教育时间越长,获得更高薪水的机会就越大
- 没有受过教育意味着失业的可能性更高
- 大学越出名,薪资越高,就业机会也越高
这合理吗?也许合理,也许不合理。关键是我们的目标是从模拟(后验)中找到这类反应。
2.1 实现
现在,我们如何在这个马尔可夫链上运行 1k、10k、100k 次模拟?
让我们一步一步来。
第一件事是导入我们需要的库。没什么特别的,我喜欢用seaborn来绘图,但这不是必需的。我相信其他库已经在 Anaconda 包中了。如果没有,一个非常简单的 pip install 就可以了 :)
import json
import random
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd让我们用这行非常简单的代码来加载 json 文件:
probability_data = json.load(open('career_decision_tree.json'))现在,让我们从头(高中毕业,绿色节点)到脚(就业/失业,红色节点)运行整个过程。在遍历树时,我们保存工时、工资和路径。由于 .json 文件中的工资只是“平均”工资,因此我们添加了一些“噪音”,在 AvgSalary 的基础上添加了 -10% 到 +10% 之间的值(可能更多,请根据您的喜好进行调整)。当然,如果我们运气不好,最终失业了,最终工资将为 0。我还将最低工资设置为 24k。
这是要运行的代码:
def simulate_path(data, state="HighSchoolGraduate"):
#update_unemployed(data)
current_state = data[state]
path = [state]
total_duration = 0
employment_probability = None
salary = None
while isinstance(current_state, dict):
next_state = random.choices(
population=list(current_state.keys()),
weights=[current_state[k]['probability'] if isinstance(current_state[k], dict) and 'probability' in current_state[k] else 0 for k in current_state.keys()],
k=1
)[0]
path.append(next_state)
if 'duration' in current_state[next_state]:
total_duration += current_state[next_state]['duration']
if 'probability' in current_state[next_state]:
employment_probability = current_state[next_state]['probability']
current_state = current_state[next_state]
if 'Employed' in current_state and 'Unemployed' in current_state:
final_state = random.choices(
population=['Employed', 'Unemployed'],
weights=[current_state['Employed']['probability'], current_state['Unemployed']['probability']],
k=1
)[0]
path.append(final_state)
if 'duration' in current_state[final_state]:
total_duration += current_state[final_state]['duration']
if 'probability' in current_state[final_state]:
employment_probability = current_state[final_state]['probability']
if 'AvgSalary' in current_state[final_state]:
#salary = np.random.choice([0,1,2,3,4])
salary = current_state[final_state]['AvgSalary']+current_state[final_state]['AvgSalary']*np.random.choice(np.arange(-0.20,0.20,0.001))
salary = max(salary,24000)
salary = salary.round(0)
break
return path, total_duration, salary现在我们可以在几秒钟内运行马尔可夫链,比如说 10 万次:
simulations = [simulate_path(probability_data) for _ in range(100_000)]
durations_employed = [simulation[1] for simulation in simulations if simulation[2]!=None]
salaries_employed = [simulation[2] for simulation in simulations if simulation[2]!=None]
paths_employed = [simulation[0] for simulation in simulations if simulation[2]!=None]
durations_unemployed = [simulation[1] for simulation in simulations if simulation[2]==None]
salaries_unemployed = [simulation[2] for simulation in simulations if simulation[2]==None]
paths_unemployed = [simulation[0] for simulation in simulations if simulation[2]==None]我已经将案例分为学业结束后找到工作的人和没有找到工作的人。
2.2 就业/失业
第一个有趣的问题是“就业/失业的百分比是多少”?
当然,根据我们在 json 文件中设置的概率,失业人数将低于就业人数。这是因为,无论你上大学还是不上大学,找到工作的概率都高于 0.5……
from collections import Counter
#counts = Counter([paths_unemployed[i][1] for i in range(len(paths_unemployed))])
#counts = Counter([len(durations_employed),100_000-len(durations_employed)])
plt.figure(figsize=(20,10))
plt.title('Employed/Unemployed Ratio')
counts = [len(durations_employed),100_000-len(durations_employed)]
labels = ['Employed','Unemployed']
colors = ['#ff9999','#66b3ff']
plt.pie(counts,labels=labels, autopct='%1.1f%%', shadow=True, startangle=140,colors = colors,textprops={'fontsize': 14})([<matplotlib.patches.Wedge at 0x7e91d311d420>,
<matplotlib.patches.Wedge at 0x7e91d324cb80>],
[Text(0.6022424133737193, -0.9204912142621452, 'Employed'),
Text(-0.6022423918280674, 0.9204912283586458, 'Unemployed')],
[Text(0.32849586184021046, -0.502086116870261, '90.7%'),
Text(-0.3284958500880367, 0.5020861245592613, '9.3%')])
因此,总体而言,正如预期的那样,失业率很低。
不过,如果你没有上过大学,失业率大约是这个数字的两倍:
num_not_college = 0
num_not_college_unemployed = 0
num_college = 0
num_college_unemployed = 0
for k in range(len(simulations)):
if simulations[k][0][1]=='DoNotGoToCollege':
num_not_college += 1
if simulations[k][0][-1] == 'Unemployed':
num_not_college_unemployed += 1
else:
num_college = num_college+1
if simulations[k][0][-1] == 'Unemployed':
num_college_unemployed += 1
unemployed_ratio_data ={'Didnt go to college': (num_not_college_unemployed/num_not_college), 'Went to College':(num_college_unemployed/num_college)}
sns.barplot(unemployed_ratio_data)
plt.ylabel('Probability of being unemployed')Text(0, 0.5, 'Probability of being unemployed')
如果你没有上过大学,那么失业的可能性约为 15%;如果你上过大学,那么失业的可能性约为 7%。
2.3 时间相关统计数据
让我们再获取一些与时间相关的统计数据。再次将人口分为就业人口和失业人口:
employment_data = pd.DataFrame([paths_employed,salaries_employed,durations_employed]).T
employment_data.columns = ['Career Path','Salary','Duration']
unemployment_data = pd.DataFrame([paths_unemployed,salaries_unemployed,durations_unemployed]).T
unemployment_data.columns = ['Career Path','Salary','Duration']我们看看这些人学了多少年了。
plt.figure(figsize=(20,10))
plt.subplot(1,2,1)
plt.title('Employed')
sns.countplot(data = employment_data, x='Duration',palette='plasma')
plt.xlabel('Years of Education')
plt.ylim(0,60_000)
plt.grid(alpha=0.4)
plt.subplot(1,2,2)
plt.title('Unemployed')
sns.countplot(data = unemployment_data, x='Duration',palette='plasma')
plt.xlabel('Years of Education')
plt.ylim(0,60_000)
plt.grid(alpha=0.4)
<ipython-input-8-52b5edee245f>:4: FutureWarning:
Passing `palette` without assigning `hue` is deprecated and will be removed in v0.14.0. Assign the `x` variable to `hue` and set `legend=False` for the same effect.
sns.countplot(data = employment_data, x='Duration',palette='plasma')
<ipython-input-8-52b5edee245f>:10: FutureWarning:
Passing `palette` without assigning `hue` is deprecated and will be removed in v0.14.0. Assign the `x` variable to `hue` and set `legend=False` for the same effect.
sns.countplot(data = unemployment_data, x='Duration',palette='plasma')

图片由作者制作
因此,大多数上过大学并就业的人都读了 4 年。另一方面,大多数失业的人根本没有上过大学(我们已经知道这一点)。
2.4 薪资统计
那么,学习 0-2 年或 4 年是否有明显的优势?薪资
方面也有明显差异:
plt.figure(figsize=(20,10))
plt.subplot(3,1,3)
plt.grid(alpha=0.2)
plt.title('After 4 years of education')
plt.hist(np.array(salaries_employed)[np.where(np.array(durations_employed)==4)])
plt.xlim(0,150_000)
plt.subplot(3,1,2)
plt.grid(alpha=0.2)
plt.title('After 2 years of education')
plt.hist(np.array(salaries_employed)[np.where(np.array(durations_employed)==2)])
plt.xlim(0,150_000)
plt.subplot(3,1,1)
plt.grid(alpha=0.2)
plt.title('After 0 years of education')
plt.hist(np.array(salaries_employed)[np.where(np.array(durations_employed)==0)])
plt.xlim(0,150_000)
学习 2 年的人最高收入为 60k,而学习 4 年的人最高收入可以为 140k。
更清楚的看待它的方式:
plt.figure(figsize=(10,6))
sns.boxenplot(x = 'Duration', y='Salary', data = employment_data)
plt.grid()
记住一件事:这些数字是编造的,所以它们本身没有任何意义。尽管如此,令人印象深刻的是,我们可以通过运行马尔可夫链并提取模拟结果来推断它们。
在这种情况下,这些虚构的数字告诉我们以下故事:学习 2 年或 4 年后找到工作的可能性几乎相同,但学习时间越长,赚更多钱的机会就越多,因为薪资分布倾向于拥有学士学位的人获得更高的薪水。
3. 结论
在这篇博文中,我们深入研究了使用马尔可夫链进行职业路径建模的迷人世界,并使用 Python 进行实践。我们从建模的基础知识开始,强调它如何结合科学和编码来近似现实世界的过程。通过模拟马尔可夫链,我们探讨了不同的教育和职业选择如何影响个人未来的工作前景和薪水。
感谢关注雲闪世界。(亚马逊aws和谷歌GCP服务协助解决云计算及产业相关解决方案)
订阅频道(https://t.me/awsgoogvps_Host)
TG交流群(t.me/awsgoogvpsHost)