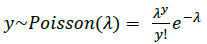手撕Leetcode个人笔记【第二周-数组-链表】

2. 两数相加

中等

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

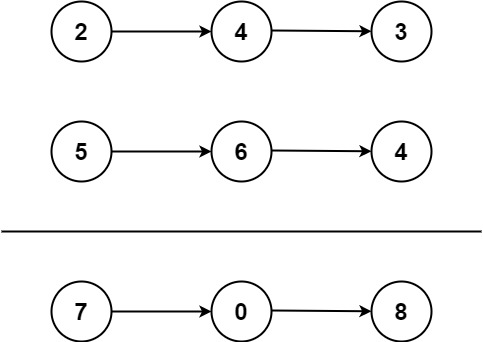
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]

示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零

struct ListNode *addTwoNumbers(struct ListNode *l1, struct ListNode *l2)
{
    struct ListNode *dummyHead = malloc(sizeof(struct ListNode)); /* 定义一个新的链表用于存储求和的结果 */
    struct ListNode *cur = dummyHead;

    /* 定义一个变量用于保存进位 */
    int carry = 0;

    while (l1 || l2 || carry) // 进位不要漏了
    {
        int sum = carry;
        if (l1 != NULL)
        {
            sum += l1->val;
            l1 = l1->next;
        }

        if (l2 != NULL)
        {
            sum += l2->val;
            l2 = l2->next;
        }

        /* 创建一个节点插入到新的链表并且值初始化为l1->val+l2->val的个位数 */
        struct ListNode *tmp = malloc(sizeof(struct ListNode));
        tmp->val = sum % 10;
        tmp->next = NULL;
        /* 插入结点tmp     因为是从头开始插入所以只需要每次更新cur */
        cur->next = tmp;
        cur = cur->next;

        /* 获取上个节点的进位值 加到下个节点的运算中 */
        carry = sum / 10;
    }

    /* 注意这里不返回dummyHead因为这里相当于一个虚拟头节点 下一个才是正真的头节点 */
    return dummyHead->next;
}

12. 整数转罗马数字

中等

七个不同的符号代表罗马数字，其值如下：

符号	值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

罗马数字是通过添加从最高到最低的小数位值的转换而形成的。将小数位值转换为罗马数字有以下规则：

如果该值不是以 4 或 9 开头，请选择可以从输入中减去的最大值的符号，将该符号附加到结果，减去其值，然后将其余部分转换为罗马数字。
如果该值以 4 或 9 开头，使用 减法形式，表示从以下符号中减去一个符号，例如 4 是 5 (V) 减 1 (I): IV ，9 是 10 (X) 减 1 (I)：IX。仅使用以下减法形式：4 (IV)，9 (IX)，40 (XL)，90 (XC)，400 (CD) 和 900 (CM)。
只有 10 的次方（I, X, C, M）最多可以连续附加 3 次以代表 10 的倍数。你不能多次附加 5 (V)，50 (L) 或 500 (D)。如果需要将符号附加4次，请使用 减法形式。

给定一个整数，将其转换为罗马数字。

示例 1：

**输入：**num = 3749

输出： “MMMDCCXLIX”

解释：

3000 = MMM 由于 1000 (M) + 1000 (M) + 1000 (M)
 700 = DCC 由于 500 (D) + 100 (C) + 100 (C)
  40 = XL 由于 50 (L) 减 10 (X)
   9 = IX 由于 10 (X) 减 1 (I)
注意：49 不是 50 (L) 减 1 (I) 因为转换是基于小数位

示例 2：

**输入：**num = 58

输出：“LVIII”

解释：

50 = L
 8 = VIII

示例 3：

**输入：**num = 1994

输出：“MCMXCIV”

解释：

1000 = M
 900 = CM
  90 = XC
   4 = IV

提示：

1 <= num <= 3999

前言

罗马数字符号

罗马数字由 7 个不同的单字母符号组成，每个符号对应一个具体的数值。此外，减法规则（如问题描述中所述）给出了额外的 6 个复合符号。这给了我们总共 13 个独特的符号（每个符号由 1 个或 2 个字母组成），如下图所示。

罗马数字的唯一表示法

让我们从一个例子入手。考虑 140 的罗马数字表示，下面哪一个是正确的？

我们用来确定罗马数字的规则是：对于罗马数字从左到右的每一位，选择尽可能大的符号值。对于 140，最大可以选择的符号值为 C=100。接下来，对于剩余的数字 40，最大可以选择的符号值为 XL=40。因此，140 的对应的罗马数字为 C+XL=CXL。

根据罗马数字的唯一表示法，为了表示一个给定的整数 num，我们寻找不超过 num 的最大符号值，将 num 减去该符号值，然后继续寻找不超过 num 的最大符号值，将该符号拼接在上一个找到的符号之后，循环直至 num 为 0。最后得到的字符串即为 num 的罗马数字表示。

编程时，可以建立一个数值-符号对的列表 valueSymbols，按数值从大到小排列。遍历 valueSymbols 中的每个数值-符号对，若当前数值 value 不超过 num，则从 num 中不断减去 value，直至 num 小于 value，然后遍历下一个数值-符号对。若遍历中 num 为 0 则跳出循环。

方法一：模拟

//法一  模拟
char* intToRoman(int num) 
{
    const int values[] = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
    const char* symbols[] = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
    char *roman = malloc(sizeof(char)*20);   // 为结果字符串分配足够的内存
    roman[0] = '\0';
    for (int i = 0; i < 13; i++) 
    {
        while (num >= values[i]) 
        { // 只要 num 大于等于当前的值
            num -= values[i]; // 减去当前的值
            strcat(roman, symbols[i]); // 将对应的符号添加到结果字符串中
        }
        if (num == 0) 
        {
            break; // 如果 num 变为 0，提前退出循环
        }
    }
    return roman; // 返回结果字符串
}

方法二：硬编码数字

思路

在这里插入图片描述

回顾前言中列出的这 13 个符号，可以发现：

千位数字只能由 M 表示；
百位数字只能由 C，CD，D 和 CM 表示；
十位数字只能由 X，XL，L 和 XC 表示；
个位数字只能由 I，IV，V 和 IX 表示。
这恰好把这 13 个符号分为四组，且组与组之间没有公共的符号。因此，整数 num 的十进制表示中的每一个数字都是可以单独处理的。

进一步地，我们可以计算出每个数字在每个位上的表示形式，整理成一张硬编码表。如下图所示，其中 0 对应的是空字符串。

利用模运算和除法运算，我们可以得到 num 每个位上的数字：

thousands_digit = num / 1000
hundreds_digit = (num % 1000) / 100
tens_digit = (num % 100) / 10
ones_digit = num % 10
最后，根据 num 每个位上的数字，在硬编码表中查找对应的罗马字符，并将结果拼接在一起，即为 num 对应的罗马数字。


// 定义罗马数字符号对应的字符串数组
const char* thousands[] = {"", "M", "MM", "MMM"};
const char* hundreds[] = {"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"};
const char* tens[] = {"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"};
const char* ones[] = {"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"};

char* intToRoman(int num) {
    char* roman = malloc(sizeof(char) * 16); // 为结果字符串分配内存
    roman[0] = '\0'; // 初始化为空字符串

    // 计算千位数并追加到结果字符串
    strcpy(roman + strlen(roman), thousands[num / 1000]);
    
    // 计算百位数并追加到结果字符串
    strcpy(roman + strlen(roman), hundreds[(num % 1000) / 100]);
    
    // 计算十位数并追加到结果字符串
    strcat(roman, tens[(num % 100) / 10]);
    
    // 计算个位数并追加到结果字符串
    strcat(roman, ones[num % 10]);

    return roman; // 返回结果字符串
}

390. 消除游戏

中等

列表 arr 由在范围 [1, n] 中的所有整数组成，并按严格递增排序。请你对 arr 应用下述算法：

从左到右，删除第一个数字，然后每隔一个数字删除一个，直到到达列表末尾。
重复上面的步骤，但这次是从右到左。也就是，删除最右侧的数字，然后剩下的数字每隔一个删除一个。
不断重复这两步，从左到右和从右到左交替进行，直到只剩下一个数字。

给你整数 n ，返回 arr 最后剩下的数字。

示例 1：

输入：n = 9
输出：6
解释：
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
arr = [2, 4, 6, 8]
arr = [2, 6]
arr = [6]

示例 2：

输入：n = 1
输出：1

//递归
int lastRemaining(int n) 
{
     return n == 1 ? 1 : 2 * (n / 2 + 1 - lastRemaining(n / 2));
}

解题思路： 1, 2, 3, 4, 5, 6, 7, 8, 9
我们可以发现这样一个规律，每一轮筛选过后，数量都会变为原来的一半，步长加倍。
比如1-9，筛选一遍后，就会变为2,4,6,8，步长为2，
在筛选一遍，就会变为2,6，步长为4，
在筛选一遍，就会变为6，则返回结果就是6。
所以我们可以设置这样几个变量去记录，
一个开始的数字start，
一个步长step，
一个遍历的次数times，
一个统计当前总数量的count。
这样每次筛选的时候，我们只要记录一个步长和一个start就好了。
当count==1的时候，start就是我们想要的结果


int lastRemaining(int n) 
{
    int start = 1;  //记录从左侧开始的位置
    int step = 1;   //步长，1变为2，变为4，变为8等等
    int count = n;  //当前的数量
    int times = 0;  //统计次数
    while ( count > 1)
    {   //从左侧开始
        if ( times % 2 == 0)
            start += step;
        else    //从右侧开始
        {
            if( count % 2 != 0)	   // 如果当前数量是奇数
                start += step;
        }
        
        count = count /2 ;         //长度减半
        step = step *2;   //步长翻一倍
        times++;
    }
    return start;
    
}

234. 回文链表

简单

给你一个单链表的头节点 head ，请你判断该链表是否为

回文链表

。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：head = [1,2,2,1]
输出：true

示例 2：

输入：head = [1,2]
输出：false

提示：

链表中节点数目在范围[1, 105] 内
0 <= Node.val <= 9

**进阶：**你能否用 O(n) 时间复杂度和 O(1) 空间复杂度解决此题？


bool isPalindrome(struct ListNode* head)
{
    if (head == NULL || head->next == NULL) 
        return true;

    typedef struct ListNode ListNode;
    ListNode *fast = head;  // 慢指针，找到链表中间分位置，作为分割
    ListNode *slow = head;
    ListNode *pre = NULL;   // 记录慢指针的前一个节点，用来分割链表

    while (fast && fast->next)
    {
        fast = fast->next->next;
        pre = slow;
        slow = slow->next;  
    }

    pre->next = NULL;   // 切断链表

    // 反转后半部分链表
    pre = NULL;

    while (slow!=NULL)
    {
        fast = slow->next;
        slow->next = pre;
        pre = slow;
        slow = fast;
    }

    // 比较前半部分和后半部分
    ListNode *head1 = head;

    ListNode *head2 = pre;
    while (head1 && head2)
    {
        if(head1->val != head2->val)
            return false;

        else
        {
            head1 = head1->next;
            head2 = head2->next;
        }
    }

    return true;

}

189. 轮转数组

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

示例 2:

输入：nums = [-1,-100,3,99], k = 2
输出：[3,99,-1,-100]
解释: 
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]

提示：

1 <= nums.length <= 105
-231 <= nums[i] <= 231 - 1
0 <= k <= 105

进阶：

尽可能想出更多的解决方案，至少有三种不同的方法可以解决这个问题。
你可以使用空间复杂度为 O(1) 的原地算法解决这个问题吗？

在字符串：剑指Offer58-II.左旋转字符串中，我们提到，如下步骤就可以左旋转字符串：

反转区间为前n的子串
反转区间为n到末尾的子串
反转整个字符串

本题是右旋转，其实就是反转的顺序改动一下，优先反转整个字符串，步骤如下：

反转整个字符串
反转区间为前k的子串
反转区间为k到末尾的子串

需要注意的是，本题还有一个小陷阱，题目输入中，如果k大于nums.size了应该怎么办？

举个例子，比较容易想，

例如，1,2,3,4,5,6,7 如果右移动15次的话，是 7 1 2 3 4 5 6 。

所以其实就是右移 k % nums.size() 次，即：15 % 7 = 1

C代码如下：

// 给定一个数组，将数组中的元素向右移动 k 个位置，其中 k 是非负数。
#include <stdio.h>

// 辅助函数，用于反转数组的一部分
void revers(int *nums, int start, int end)
{
    while (start < end)
    {
        int temp = nums[start];
        nums[start] = nums[end];
        nums[end] = temp;
        start++;
        end--;
    }
}

// 主函数，实现数组的旋转
void rotate(int *nums, int numsSize, int k)
{
    k = k % numsSize;
    revers(nums, 0, numsSize - 1);
    revers(nums, 0, k - 1);
    revers(nums, k , numsSize - 1);
}

// 测试函数
int main(int argc, char const *argv[])
{
    int nums[] = {1, 2, 3, 4, 5, 6, 7};
    int numsSize = sizeof(nums) / sizeof(nums[0]);
    int k = 3;

    rotate(nums, numsSize, k);

    for (int i = 0; i < numsSize; i++)
    {
        printf("%d\t", nums[i]);
    }

    return 0;
}

203. 移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

示例 1：

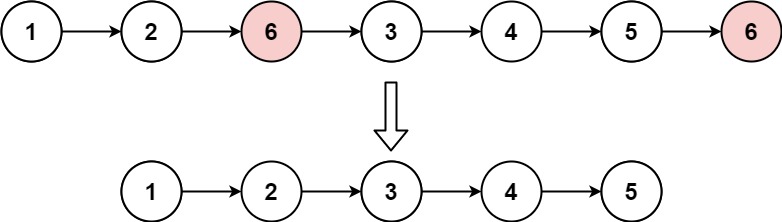
输入：head = [1,2,6,3,4,5,6], val = 6
输出：[1,2,3,4,5]

示例 2：

输入：head = [], val = 1
输出：[]

示例 3：

输入：head = [7,7,7,7], val = 7
输出：[]

提示：

列表中的节点数目在范围 [0, 104] 内
1 <= Node.val <= 50
0 <= val <= 50

#include<stdio.h>
#include<stdlib.h>
typedef struct ListNode
{
    int val;
    struct ListNode *next;
}ListNode;

//用原来的链表操作：
struct ListNode* removeElements(struct ListNode* head, int val)
{
    struct ListNode* temp;
    // 当头结点存在并且头结点的值等于val时
    while(head && head->val == val) 
    {
        temp = head;
        // 将新的头结点设置为head->next并删除原来的头结点
        head = head->next;
        free(temp);
    }

    struct ListNode *cur = head;
    // 当cur存在并且cur->next存在时
    // 此解法需要判断cur存在因为cur指向head。若head本身为NULL或者原链表中元素都为val的话，cur也会为NULL
    while(cur && (temp = cur->next)) 
    {
        // 若cur->next的值等于val
        if(temp->val == val) 
        {
            // 将cur->next设置为cur->next->next并删除cur->next
            cur->next = temp->next;
            free(temp);
        }
        // 若cur->next不等于val，则将cur后移一位
        else
            cur = cur->next;
    }

    // 返回头结点
    return head;
}

//设置一个虚拟头结点：
struct ListNode* removeElements1(struct ListNode* head, int val) {
    // 定义结构体类型 ListNode
    typedef struct ListNode ListNode;
    
    // 创建一个新的节点 shead，并初始化
    ListNode *dummy = (ListNode *)malloc(sizeof(ListNode));
    
    // 将新节点的 next 指针指向传入的 head
    dummy->next = head;
    
    // 定义一个当前指针 cur，初始化指向 shead
    ListNode *cur = dummy;
    
    // 遍历链表，直到 cur 的 next 指针为空
    while (cur->next != NULL) {
        // 如果 cur 的下一个节点的值等于给定的 val
        if (cur->next->val == val) {
            // 临时存储要删除的节点
            ListNode *tmp = cur->next;
            // 将 cur 的 next 指针跳过下一个节点，指向下下个节点
            cur->next = cur->next->next;
            // 释放被删除节点的内存
            free(tmp);
        } else {
            // 如果值不相等，cur 指向下一个节点
            cur = cur->next;
        }
    }
    
    // 更新 head，指向实际的头节点
    head = dummy->next;
    // 释放辅助节点 shead 的内存
    free(dummy);
    
    // 返回更新后的头节点
    return head;
}


// 打印链表
void printList(struct ListNode* head) {
    struct ListNode* temp = head;
    while (temp) {
        printf("%d -> ", temp->val);
        temp = temp->next;
    }
    printf("NULL\n");
}

// 创建新节点
struct ListNode* createNode(int val) {
    struct ListNode* newNode = (struct ListNode*)malloc(sizeof(struct ListNode));
    newNode->val = val;
    newNode->next = NULL;
    return newNode;
}

int main() {
    // 创建链表 1 -> 2 -> 6 -> 3 -> 4 -> 5 -> 6
    struct ListNode* head = createNode(1);
    head->next = createNode(2);
    head->next->next = createNode(6);
    head->next->next->next = createNode(3);
    head->next->next->next->next = createNode(4);
    head->next->next->next->next->next = createNode(5);
    head->next->next->next->next->next->next = createNode(6);
    
    printf("Original list: ");
    printList(head);
    
    // 删除所有值为6的节点
    head = removeElements1(head,6);
    
    printf("Modified list: ");
    printList(head);
    
    // 释放链表内存
    while (head) {
        struct ListNode* temp = head;
        head = head->next;
        free(temp);
    }
    
    return 0;
}

! 707. 设计链表

中等

你可以选择使用单链表或者双链表，设计并实现自己的链表。

单链表中的节点应该具备两个属性：val 和 next 。val 是当前节点的值，next 是指向下一个节点的指针/引用。

如果是双向链表，则还需要属性 prev 以指示链表中的上一个节点。假设链表中的所有节点下标从 0 开始。

实现 MyLinkedList 类：

MyLinkedList() 初始化 MyLinkedList 对象。
int get(int index) 获取链表中下标为 index 的节点的值。如果下标无效，则返回 -1 。
void addAtHead(int val) 将一个值为 val 的节点插入到链表中第一个元素之前。在插入完成后，新节点会成为链表的第一个节点。
void addAtTail(int val) 将一个值为 val 的节点追加到链表中作为链表的最后一个元素。
void addAtIndex(int index, int val) 将一个值为 val 的节点插入到链表中下标为 index 的节点之前。如果 index 等于链表的长度，那么该节点会被追加到链表的末尾。如果 index 比长度更大，该节点将 不会插入 到链表中。
void deleteAtIndex(int index) 如果下标有效，则删除链表中下标为 index 的节点。

示例：

输入
["MyLinkedList", "addAtHead", "addAtTail", "addAtIndex", "get", "deleteAtIndex", "get"]
[[], [1], [3], [1, 2], [1], [1], [1]]
输出
[null, null, null, null, 2, null, 3]

解释
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addAtHead(1);
myLinkedList.addAtTail(3);
myLinkedList.addAtIndex(1, 2);    // 链表变为 1->2->3
myLinkedList.get(1);              // 返回 2
myLinkedList.deleteAtIndex(1);    // 现在，链表变为 1->3
myLinkedList.get(1);              // 返回 3

提示：

0 <= index, val <= 1000
请不要使用内置的 LinkedList 库。
调用 get、addAtHead、addAtTail、addAtIndex 和 deleteAtIndex 的次数不超过 2000 。

#include <stdio.h>
#include <stdlib.h>

// 定义链表节点结构
typedef struct MyLinkedList {
    int val;
    struct MyLinkedList *next;
} MyLinkedList;

/*
 * myLinkedListCreate : 创建链表
 * 返回值：
 *   链表头节点
 */
MyLinkedList* myLinkedListCreate() {
    MyLinkedList *head = (MyLinkedList *)malloc(sizeof(MyLinkedList)); // 为链表头节点分配内存
    head->next = NULL; // 初始化next指针为NULL
    return head; // 返回链表头节点
}

/*
 * myLinkedListGet : 获取第n个节点的值
 * 参数：
 *   obj    ：   链表头节点
 *   index  :    要获取值的节点下标，从0开始
 * 返回值：
 *    成功  :  节点的值
 *    失败  :  -1
 */
int myLinkedListGet(MyLinkedList *obj, int index) {
    MyLinkedList *cur = obj->next; // 跳过头节点
    for (int i = 0; cur != NULL; i++) { // 遍历链表
        if (i == index) { // 找到目标节点
            return cur->val; // 返回节点值
        }
        cur = cur->next; // 移动到下一个节点
    }
    return -1; // 下标超出范围，返回-1
}

/*
 * myLinkedListAddAtHead : 头部插入节点
 * 参数：
 *   obj    ：   链表头节点
 *   val    :    插入值
 * 返回值：
 *    无
 */
void myLinkedListAddAtHead(MyLinkedList *obj, int val) {
    MyLinkedList *nhead = (MyLinkedList *)malloc(sizeof(MyLinkedList)); // 为新节点分配内存
    nhead->val = val; // 设置新节点的值
    nhead->next = obj->next; // 新节点指向当前头节点的下一个节点
    obj->next = nhead; // 头节点指向新节点
}

/*
 * myLinkedListAddAtTail : 尾部插入节点
 * 参数：
 *   obj    ：   链表头节点
 *   val    :    插入值
 * 返回值：
 *    无
 */
void myLinkedListAddAtTail(MyLinkedList *obj, int val) {
    MyLinkedList *cur = obj; // 初始化cur指针为头节点
    while (cur->next != NULL) { // 遍历链表找到尾节点
        cur = cur->next;
    }
    MyLinkedList *ntail = (MyLinkedList *)malloc(sizeof(MyLinkedList)); // 为新节点分配内存
    ntail->val = val; // 设置新节点的值
    ntail->next = NULL; // 新节点的next指针为NULL
    cur->next = ntail; // 当前尾节点的next指向新节点
}

/*
 * myLinkedListAddAtIndex : 第n个节点前插入节点
 * 参数：
 *   obj    ：   链表头节点
 *   index  :    插入位置
 *   val    :    插入值
 * 返回值：
 *    无
 */
void myLinkedListAddAtIndex(MyLinkedList *obj, int index, int val) {
    if (index == 0) { // 如果插入位置是头节点
        myLinkedListAddAtHead(obj, val); // 调用头部插入函数
        return;
    }
    MyLinkedList *cur = obj->next; // 跳过头节点
    for (int i = 1; cur != NULL; i++) { // 遍历链表
        if (index == i) { // 找到目标位置
            MyLinkedList *newNode = (MyLinkedList *)malloc(sizeof(MyLinkedList)); // 为新节点分配内存
            newNode->val = val; // 设置新节点的值
            newNode->next = cur->next; // 新节点的next指向当前节点的下一个节点
            cur->next = newNode; // 当前节点的next指向新节点
            return;
        }
        cur = cur->next; // 移动到下一个节点
    }
}

/*
 * myLinkedListDeleteAtIndex : 删除第n个节点
 * 参数：
 *   obj    ：   链表头节点
 *   index  :    删除位置
 * 返回值：
 *    无
 */
void myLinkedListDeleteAtIndex(MyLinkedList *obj, int index) {
    if (index == 0) { 	// 如果删除的是头节点后的第一个节点
        MyLinkedList *tmp = obj->next; // 暂存该节点
        if (tmp != NULL) {
            obj->next = tmp->next; // 头节点的next指向该节点的下一个节点
            free(tmp); // 释放该节点的内存
        }
        return;
    }
    MyLinkedList *cur = obj->next; // 跳过头节点
    for (int i = 1; cur != NULL && cur->next != NULL; i++) { // 遍历链表
        if (i == index) { // 找到目标位置
            MyLinkedList *tmp = cur->next; // 暂存要删除的节点
            if (tmp != NULL) {
                cur->next = tmp->next; // 当前节点的next指向要删除节点的下一个节点
                free(tmp); // 释放要删除节点的内存
            }
            return;
        }
        cur = cur->next; // 移动到下一个节点
    }
}

/*
 * myLinkedListFree : 销毁链表
 * 参数：
 *   obj    ：   链表头节点
 * 返回值：
 *    无
 */
void myLinkedListFree(MyLinkedList *obj) {
    while (obj != NULL) { // 遍历链表
        MyLinkedList *tmp = obj; // 暂存当前节点
        obj = obj->next; // 移动到下一个节点
        free(tmp); // 释放当前节点的内存
    }
}

int main() {
    // 创建链表
    MyLinkedList* obj = myLinkedListCreate();
    // 头部插入1
    myLinkedListAddAtHead(obj, 1);
    // 尾部插入3
    myLinkedListAddAtTail(obj, 3);
    // 第1个节点前插入2
    myLinkedListAddAtIndex(obj, 1, 2);
    // 获取第1个节点的值，应该是2
    printf("%d\n", myLinkedListGet(obj, 1)); // 输出 2
    // 删除第1个节点
    myLinkedListDeleteAtIndex(obj, 1);
    // 获取第1个节点的值，应该是3
    printf("%d\n", myLinkedListGet(obj, 1)); // 输出 3
    // 销毁链表
    myLinkedListFree(obj);
    return 0;
}

21. 合并两个有序链表

简单

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

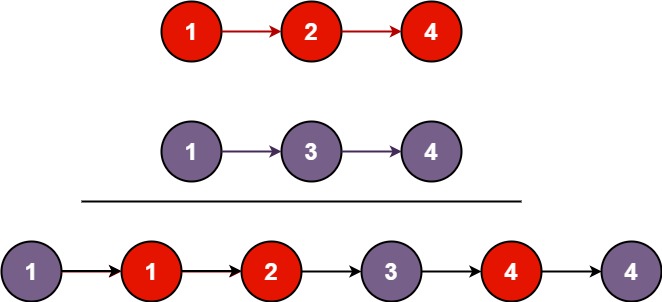
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

方法一：递归调用


struct ListNode* mergeTwoListsRecursive(struct ListNode* l1, struct ListNode* l2) 
{
    if (l1 == NULL) 
    {  // 如果l1为空，直接返回l2
        return l2;
    } 
    else if (l2 == NULL) 
    {  // 如果l2为空，直接返回l1
        return l1;
    } 
    else if (l1->val < l2->val) 
    {  // 如果l1的值小于l2的值
        l1->next = mergeTwoListsRecursive(l1->next, l2);  // l1的下一个节点指向合并后的链表
        return l1;  // 返回l1作为新的头节点
    } 
    else 
    {  // 如果l2的值小于等于l1的值
        l2->next = mergeTwoListsRecursive(l1, l2->next);  // l2的下一个节点指向合并后的链表
        return l2;  // 返回l2作为新的头节点
    }
}

方法二：虚拟头节点


struct ListNode* mergeTwoLists(struct ListNode* list1, struct ListNode* list2) 
{
    // 创建一个虚拟头节点
    struct ListNode *dummy = (struct ListNode*)malloc(sizeof(struct ListNode));
    struct ListNode* cur = dummy;  // 初始化当前指针指向虚拟节点
    struct ListNode *l1 = list1;  
    struct ListNode *l2 = list2;

    // 当两个链表都不为空时，比较节点值并合并
    while (l1 && l2) 
    {
        if (l1->val < l2->val) 
        {
            cur->next = l1;  // 当前节点指向l1
            l1 = l1->next;  // l1移动到下一个节点
        } else 
        {
            cur->next = l2;  // 当前节点指向l2
            l2 = l2->next;  // l2移动到下一个节点
        }
        cur = cur->next;  // 当前指针移动到下一个节点
    }

    // 如果l1不为空，将剩余的l1节点链接到当前指针
    if (l1 != NULL) 
    {
        cur->next = l1;
    } else 
    {  // 如果l2不为空，将剩余的l2节点链接到当前指针
        cur->next = l2;
    }

    cur = dummy->next;  // 保存合并后的链表头节点
    free(dummy);  // 释放虚拟头节点的内存
    return cur;  // 返回合并后的链表头节点
}

206. 反转链表

简单

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

提示：

链表中节点的数目范围是 [0, 5000]
-5000 <= Node.val <= 5000

**进阶：**链表可以选用迭代或递归方式完成反转。你能否用两种方法解决这道题？

思路

如果再定义一个新的链表，实现链表元素的反转，其实这是对内存空间的浪费。

其实只需要改变链表的next指针的指向，直接将链表反转，而不用重新定义一个新的链表，如图所示:

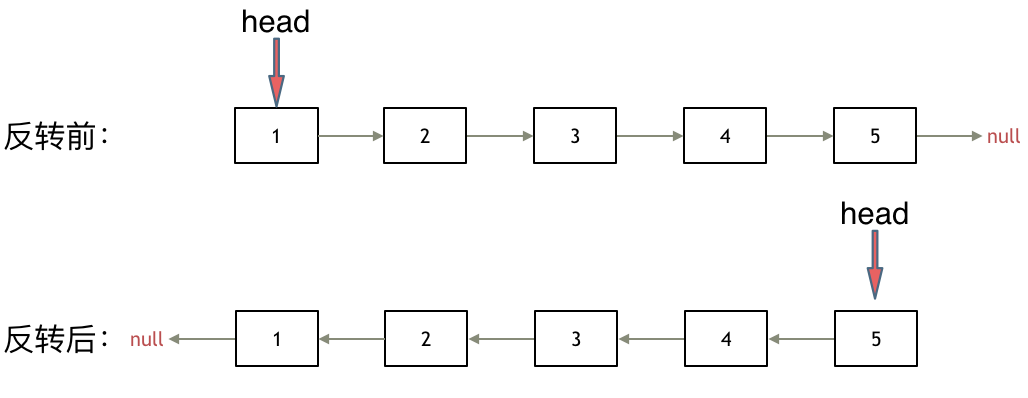
206_反转链表

之前链表的头节点是元素1，反转之后头结点就是元素5 ，这里并没有添加或者删除节点，仅仅是改变next指针的方向。

那么接下来看一看是如何反转的呢？

我们拿有示例中的链表来举例，如动画所示：（纠正：动画应该是先移动pre，在移动cur）

在这里插入图片描述

//双指针法
struct ListNode* reverseList(struct ListNode* head) 
{
    struct ListNode *pre = NULL;	
    struct ListNode *cur = head;
    
    while (cur!=NULL)
    {
        struct ListNode *tmp = cur->next;
        cur->next = pre; //改变方向
        pre = cur;		//先移动pre，在移动cur
        cur = tmp;
    }
     
    return pre;
}

//递归
struct ListNode* reverse(struct ListNode* cur, struct ListNode* pre) 
{
    if(cur == NULL)
        return pre;
    struct ListNode*tmp = cur->next;
	cur->next = pre;	//改变方向
    return reverse(tmp,cur);
}

struct ListNode* reverseList(struct ListNode* head) 
{
    return reverse(head,NULL);
}

141. 环形链表

简单

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例 1：

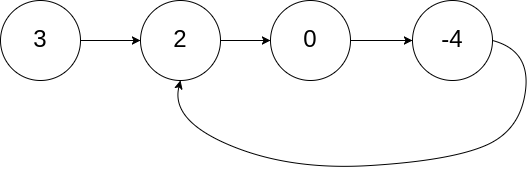
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

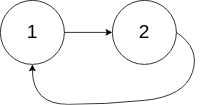
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

**进阶：**你能用 O(1)（即，常量）内存解决此问题吗？

bool hasCycle(struct ListNode* head) {
    if (head == NULL || head->next == NULL) {
        return false;
    }
    struct ListNode* slow = head;
    struct ListNode* fast = head->next;
    while (slow != fast) {
        if (fast == NULL || fast->next == NULL) {
            return false;
        }
        slow = slow->next;
        fast = fast->next->next;
    }
    return true;
}

24. 两两交换链表中的节点

中等

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

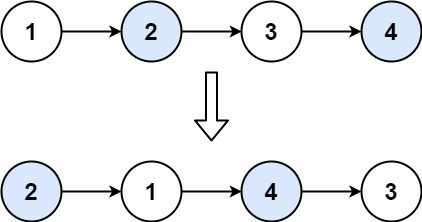
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

//使用中间变量
struct ListNode* swapPairs(struct ListNode* head) 
{
    struct ListNode *DummyHead = malloc(sizeof(struct ListNode));

    DummyHead->next = head;
    struct ListNode *cur = DummyHead;  //cur指向虚拟头节点

    while (cur->next != NULL && cur->next->next != NULL)
    {
        struct ListNode *tmp = cur->next;
        struct ListNode *tmp1 = cur->next->next->next; //保存节点，防止丢失

        // 交换
        cur->next = cur->next->next;    
        cur->next->next = tmp;
        tmp->next = tmp1;

        cur = cur->next->next;    //更新cur
    }
    
    head = DummyHead ->next;
    return head;

}

//迭代版本
struct ListNode* swapPairs(struct ListNode* head)
{
    //使用双指针避免使用中间变量
    typedef struct ListNode ListNode;
    ListNode *DummyHead = (ListNode *)malloc(sizeof(ListNode));

    DummyHead->next = head;
    ListNode *left = DummyHead;
    ListNode *right = DummyHead->next;

    while (left && right && right->next)
    {
        left->next = right->next;
        right->next = left->next->next;
        left->next->next = right;

        left = right;
        right = left->next;  
    }
    
    return DummyHead->next;
}

//递归版本
struct ListNode* swapPairs(struct ListNode* head)
{
    //递归结束条件：头节点不存在或头节点的下一个节点不存在。此时不需要交换，直接返回head
    if(!head || !head->next)
        return head;
    //创建一个节点指针类型保存头结点下一个节点
    struct ListNode *newHead = head->next;
    //更改头结点+2位节点后的值，并将头结点的next指针指向这个更改过的list
    head->next = swapPairs(newHead->next);
    //将新的头结点的next指针指向老的头节点
    newHead->next = head;
    return newHead;
}

19. 删除链表的倒数第 N 个结点

中等

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

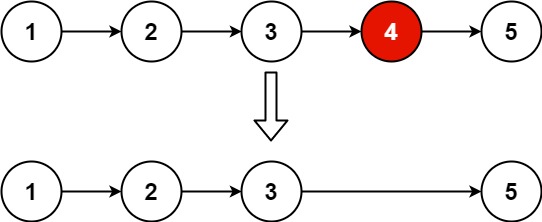
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

// 删除链表倒数第n个元素
struct ListNode *removeNthFromEnd(struct ListNode *head, int n)
{
    typedef struct ListNode ListNode;
    ListNode *DummyHead = (ListNode *)malloc(sizeof(ListNode));
    DummyHead->val = 0;
    DummyHead->next = head;

    // 定义 fast slow 双指针
    ListNode *fast = DummyHead;
    ListNode *slow = DummyHead;

    n++;
    while (n-- && fast != NULL)
        fast = fast->next;

    while (fast)
    {
        fast = fast->next;
        slow = slow->next;
    }
    ListNode *tmp = slow->next;
    slow->next = slow->next->next; // 删除倒数第n个节点
    free(tmp);

    head = DummyHead->next;
    free(DummyHead); // 删除虚拟头节点

    return head;
}