【Python实战因果推断】60_随机实验与统计知识2

news2024/12/26 9:24:52

An A/B Testing Example

在许多公司中，一种常见的策略是提供廉价甚至免费的产品，这种产品本身可能并不盈利，但其目的是吸引新客户。一旦公司获得了这些客户，就可以向他们推销其他更盈利的产品，这一过程被称为交叉销售。假设你在一个咖啡配送公司工作，公司的主打产品是一种低成本的月度订阅服务，允许客户每周收到高质量、精心挑选的咖啡。除了这个基本且成本较低的订阅服务外，公司还提供一种更高端的订阅服务，包含优质的冲泡体验以及来自世界各地的顶级咖啡，例如巴西小镇Divinolandia的本地生产者提供的咖啡。这是公司最赚钱的服务，因此你的目标是增加向已经订阅了低成本入门产品的用户销售这项高端服务的数量。为此，公司有一个营销团队，主要通过发送交叉销售邮件来推销高端咖啡订阅服务。

作为因果推断专家，你的任务是评估这些邮件的有效性。当你查看现有的（非随机化）数据以回答这个问题时，可以明显看到收到邮件的客户更有可能购买高端订阅服务。在技术术语中，当客户购买你正在推销的产品时，可以说他们转化了。因此，可以说收到邮件的客户转化率更高：

$E[Conversion|Email=1]>E[Conversion|Email=0]$

不幸的是，你还发现营销团队倾向于向那些他们认为一开始更有可能转化的客户发送邮件。具体他们是如何做到这一点的并不完全清楚。也许他们寻找与公司互动最多的客户，或者是在满意度调查中给予积极反馈的客户。无论如何，这是一个强烈的信号，表明即使不发送邮件，

$E\big[Conversion_0\big|Email=1\big]>E\big[Conversion_0\big|Email=0\big].$

换句话说，即使不发送任何邮件，实际上被发送了邮件的客户群体会比其他客户群体有更高的转化率。因此，简单的平均值比较是无法准确估计交叉销售邮件的真实因果效应的，因为这样的比较是有偏见的。为了解决这个问题，你需要让接受处理和未接受处理的两组客户变得可比：

$E\bigl[Y_{0}\bigr|T=1\bigr]=E\bigl[Y_{0}\bigr|T=0\bigr]$

这可以通过随机分配邮件来实现。如果你成功做到了这一点，那么平均而言，接受处理和未接受处理的两组客户除了受到的处理（即是否发送邮件）之外，在转化率上应该是相同的。于是，假设你确实这样做了。你从客户基础中随机选择了三个样本。对其中一个样本，你没有发送任何邮件；对另一个样本，你发送了一封内容丰富、精心撰写的关于高端订阅的邮件；对最后一个样本，你发送了一封简短而直接的关于高端订阅的邮件。收集了一段时间的数据后，你得到了以下的结果：

 import pandas as pd # for data manipulation
 import numpy as np # for numerical computation
 data = pd.read_csv("./data/cross_sell_email.csv")
 data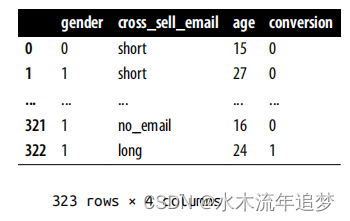

你看到总共有323个观测值。虽然算不上大数据，但已经足够进行分析了。

为了估计因果效应，你只需简单计算每个处理组的平均转化率：

 (data
 .groupby(["cross_sell_email"])
 .mean())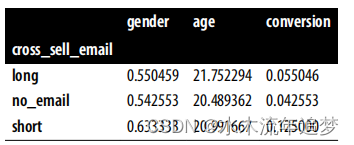

确实就是这么简单。你可以看到，没有收到邮件的那组客户转化率为4.2%，而分别收到长邮件和短邮件的两组客户的转化率分别为5.5%和惊人的12.5%。因此，平均治疗效应（ATE），即每个治疗组与控制组之间的差异，计算公式为： $ATE=E[Y|T=t]-E[Y|T=0]$ ，对于长邮件和短邮件组，分别提高了1.3和8.3个百分点。

有趣的是，发送简洁明了的邮件似乎比精心编排的长邮件效果更好。

RCT（随机对照试验）的美妙之处在于，你不再需要担心营销团队是否以某种方式针对了可能转化的客户，也不必担心来自不同治疗组的客户在系统上存在任何差异，除了他们所接受的治疗外。按设计，随机实验旨在消除这些差异，使 Y0 和 Y1 在 T 上保持独立，至少理论上如此。

实践中，一个合理的检查方法是看随机化是否正确执行（或者你是否查看了正确的数据），即检查治疗前变量中治疗组与非治疗组是否相等。例如，你有性别和年龄的数据，可以查看这两个特征在各治疗组之间是否均衡。

当你查看年龄时，治疗组看起来非常相似，但在性别方面似乎存在差异（女性=1，男性=0）。收到短邮件的组别中，男性占比达到63%，相比之下，控制组和长邮件组的男性比例分别为54%和55%。这让人有些不安，因为你在转化效果最大的治疗组中发现了这种差异。即便在理论上RCT应该保证独立性，但实际上并不一定成立。你看到的短邮件产生大效果可能是因为某种原因，男性客户的基础转化率 E[Y0|man] 大于女性客户 E[Y0|woman]。

评价平衡性并没有明确的共识，但一个简单的建议是检查治疗组之间的标准化差异： $\frac{\hat{\mu}_{tr}-\hat{\mu}_{co}}{\sqrt{\left(\hat{\sigma}_{tr}^{2}+\hat{\sigma}_{co}^{2}\right)/2}},$

其中 μ 和 σ^2 分别代表样本均值和方差。由于你的例子中有三个治疗组，你只需计算相对于控制组的这个差异：

 X = ["gender", "age"]
 mu = data.groupby("cross_sell_email")[X].mean()
 var = data.groupby("cross_sell_email")[X].var()
 norm_diff = ((mu - mu.loc["no_email"])/
 np.sqrt((var + var.loc["no_email"])/2))
 norm_diff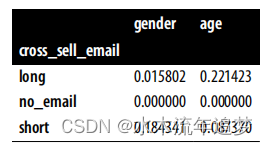

如果这个差异太小或太大，你应该感到担忧。遗憾的是，没有一个明确的阈值来界定多大的差异是过多的，但0.5似乎是一个不错的经验法则。在这个例子中，你没有任何差异达到这么高的水平，但是短邮件组在性别上的差异较大，而长邮件组在年龄上的差异较大。

如果上述公式现在看来有些神奇，不必担心。一旦你复习完统计学部分，它会变得更清晰。现在，我只想提醒你注意小数据集下可能发生的情况。即使在随机化下，也有可能某个组由于偶然性与另一组不同。在大样本中，这种差异往往趋于消失。这也引出了一个议题：多大的差异足以让你得出结论，即治疗确实是有效的，而不仅仅是因为偶然性，这是接下来我将要讨论的内容

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1953884.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！