机试中存在部分涉及到较复杂数字的问题,这是编码的基本功,各位一定要得心应手。

目录
一.最大公约数和最小公倍数
1.最大公约数
2.最小公倍数
二.素数
1.判断指定数
2.输出所有素数
3.精进不休——埃拉托斯特尼筛法
4.达到更优!——欧拉筛法
一.最大公约数和最小公倍数
初学就开始的老生常谈,比较基础,大一期末考试和普通学校考研的难度,一定不要掉以轻心。
1.最大公约数
这里我们用欧几里得算法来实现——其实也就是初中学过的辗转相除法,没什么难度~
int gcb(int x,int y)
{
if(x<y) //保证前者更大一些
{
int temp=x;
x=y;
y=temp;
}
while(y!=0)
{
int temp=y;
y=x%y;
x=temp;
}
return x;
}2.最小公倍数
设最大公约数是z,则x和y的最小公倍数就是x*y/z,这个公式也是小学知识,不要忘了;要是考试的时候真不小心忘了,就用暴力枚举吧,从x和y大的一个开始直到第一个可以同时整除x和y的元素即为最小公倍数~
int main() {
int x=0,y=0;
cout<<"请输入两个数:";
cin>>x>>y;
cout<<"最大公约数是:"<<gcb(x,y)<<endl;
cout<<"最小公倍数是:"<<(x*y)/gcb(x,y)<<endl;
}没什么问题:

二.素数
1.判断指定数
常规的暴力枚举复杂度度为O(N),其实有更为简洁的办法——即对目标数开根号,比如对于16来说,2就是其的一个约数,但是16/2也是其一个约数,显然我们并不需要枚举到8——因为对于一个数来说,既然能整除,那么约数肯定是成对出现的,因此其中一个肯定比16开根号小,另一个则肯定大,所以我们只需要枚举到4(也就是开根号),就能判断目标数字是否为素数~
bool IsPrime(int x)
{
int temp=sqrt(x);
for(int i=2;i<=temp;i++)
if(x%i==0)
return false;
return true;
}非常简单,不再赘述~
2.输出所有素数
上面函数已经有了,我们只需要枚举范围内的元素并调用函数,即可输出全部的素数:
int main() {
int x=0;
cout<<"请输入查询的最大值:";
cin>>x;
int count=0;
for(int i=1;i<=x;i++)
{
if(IsPrime(i))
{
cout<<i<<" ";
count++;
}
if(count==5)
{
cout<<endl;
count=0;
}
}
}没什么bug,count是为了输出更美观附加的:

3.精进不休——埃拉托斯特尼筛法
不妨这样思考一下:假设2是素数的话,那么他的倍数——4/6/8/10等等,一切可以整除2的数——是不是都不是素数!因此当我们找到一个素数时,如果将他的全部倍数都标记为合数,岂不是大大增加了效率。事实上,这就是埃拉托斯特尼筛法,其复杂度为LogN的平方,复杂度还要小于前面的N*根号N!代码如下:
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
void Eratos(int x)
{
vector<int> Num,answer;
Num.push_back(-1);//统一vector中的数字与下标
for(int i=1;i<=x;i++)
Num.push_back(0); //初始化数组,如果下标i是0,则代表i是素数
for(int i=2;i<x;i++)
{
if(Num[i]==0)
{
answer.push_back(i);
for(int j=i+i;j<x;j+=i)//如果i是素数,则i所有的倍数都不是素数!
Num[j]=1;
}
}
for(int k=0;k<=answer.size()-1;k++)
cout<<answer[k]<<" ";
}
int main() {
int x=0;
cout<<"请输入查询的最大值:";
cin>>x;
Eratos(x);
}没什么问题:

诸位不妨仔细品味一下这个筛选的方法及其实现——是不是又有散列,又有二分的思想?何其妙哉~
4.达到更优!——欧拉筛法
实际上,埃拉托斯特尼筛法还是有其优化的余地:比如6、10两个数字:按照其规则,这两个数在2的时候已经判断不是素数了,但是当枚举到3和5的时候,实际上还要再判断一次!
因此不妨保证——每个合数只是被自己最小的质因数找到,这样就避免了重复的筛选步骤。为了防止大家晕,这里修改一下埃式筛的代码:
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
void Eratos(int x)
{
int times=0;
int count=0;//记录当前素数的个数
vector<int> answer;//存放所有的素数
vector<int> Num;//标记
Num.push_back(0);//统一下标和数字大小
for(int i=1;i<=x;i++)
Num.push_back(0);
for(int i=2;i<=x;++i)
{
if(!Num[i])
{
answer.push_back(i);
count++;
}
for(int j=0;j<count;++j)
{
if(i*answer[j]>x)
break;
int temp=i*answer[j];
Num[temp]=1;
times++;
// if (i % answer[j] == 0)
// break;
}
}
for(int k=0;k<=answer.size()-1;k++)
cout<<answer[k]<<" ";
cout<<endl;
cout<<"共标记了:"<<times<<"次!";
}
int main() {
int x=0;
cout<<"请输入查询的最大值:";
cin>>x;
Eratos(x);
}我们来测试一下100,可以发现标记合数的步骤一共执行了104次:

我们仔细回溯一下如上代码的运行流程:
- 当i=2时,是素数,因此放到answer数组中;接下来遍历answer数组,2*2=4,因此4肯定不是素数,标记为合数
- 接下来i=3,是素数,因此放到answer数组中;接下来遍历answer,3*2=6,3*3=9,因此6和9均被标记为合数
- 接下来i=4,不是素数,直接遍历answer,2*4=8,3*4=12,8应该被标记为合数,但是对于12,其最小约数是2,因此应该由6*2来标记,所以此刻应该直接跳过
因此就有了有欧拉的写法:
void Eratos(int x)
{
int times=0;
int count=0;//记录当前素数的个数
vector<int> answer;//存放所有的素数
vector<int> Num;//标记
Num.push_back(0);//统一下标和数字大小
for(int i=1;i<=x;i++)
Num.push_back(0);
for(int i=2;i<=x;++i)
{
if(!Num[i])
{
answer.push_back(i);
count++;
}
for(int j=0;j<count;++j)
{
if(i*answer[j]>x)
break;
int temp=i*answer[j];
Num[temp]=1;
times++;
if (i % answer[j] == 0)
break;
}
}
for(int k=0;k<=answer.size()-1;k++)
cout<<answer[k]<<" ";
cout<<endl;
cout<<"共标记了:"<<times<<"次!";
}核心在于这个:大家自行品味妙处——对于上面来说,因为4已经遇到了最小质因数2,因此应该直接跳出循环!

运行100以内的素数,只执行了74次!

我们再来拿1000测试一下:

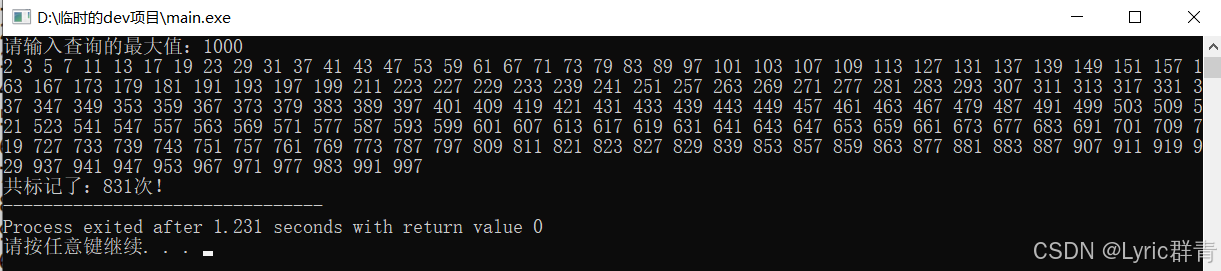
埃氏筛用了1400多次,而欧式筛只用了800多次,高低立判!
今天就先总结到这,希望如上的素数搜索,对各位思考算法的意义有所启发——当人力无法计算庞大的运算量时,计算机应运而生;而计算机由于计算方式的不同,效率也不尽相同。我们追求高效简洁的算法,因为越低的耗时标志着越高的生产力——而相信各位都学过马克思主义基本原理:社会变革的根本原因是生产力的发展~博主有幸拜读过《人月神话》,相信大家都清楚【银弹】对于软件工程的意义。或许对于银弹的不懈追求,正是人类能够进化的原因~





![[C#]调用本地摄像头录制视频并保存](https://i-blog.csdnimg.cn/direct/7cbeca119e20435a93829ed002cd316f.png)