一、二叉搜索树中的插入操作

题目：

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

示例 1：

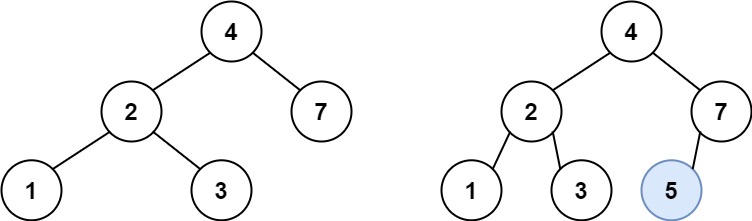
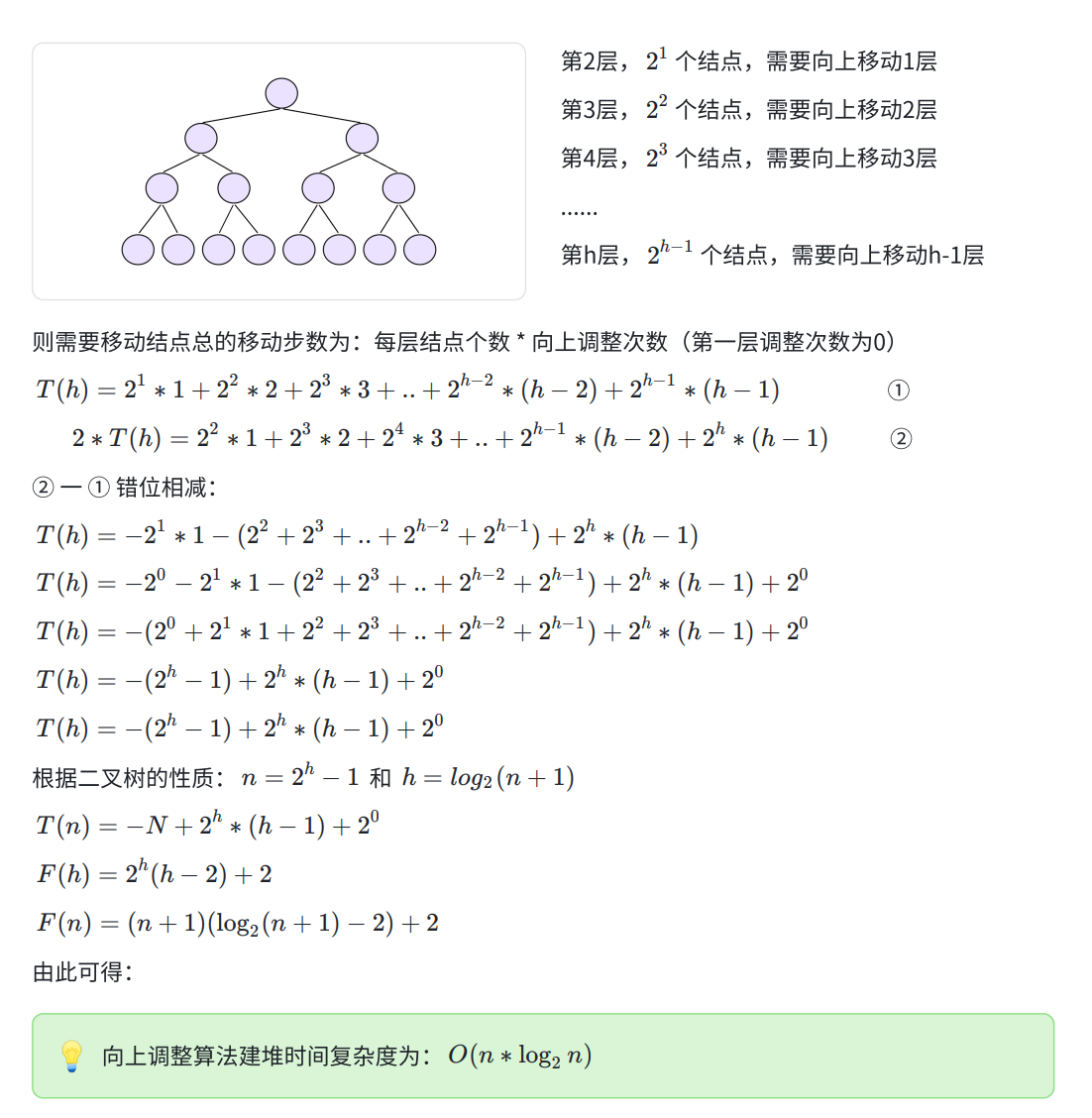
输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

 思路：

只需要按照二叉搜索树的规则，遇到空节点时创建新的节点并插入即可，不需要去刻意的改变树的结构

代码：

public TreeNode insertIntoBST(TreeNode root, int val) {
    // 如果根节点为空，直接创建一个新节点作为根节点并返回
    if (root == null) {
        return new TreeNode(val);
    }
    
    // 如果插入值小于当前节点的值，递归地将值插入到左子树
    if (val < root.val) {
        root.left = insertIntoBST(root.left, val);
    }
    
    // 如果插入值大于当前节点的值，递归地将值插入到右子树
    if (val > root.val) {
        root.right = insertIntoBST(root.right, val);
    }
    
    // 返回根节点
    return root;
}

• 如果当前根节点 root 为空，说明当前位置可以插入新节点 val，因此创建一个新的 TreeNode 对象并返回，这个节点成为新的根节点。
• 如果插入值 val 小于当前节点 root 的值，则将 val 插入到当前节点的左子树中。递归调用 insertIntoBST 方法，将返回的左子树根节点赋值给 root.left。
• 如果插入值 val 大于当前节点 root 的值，则将 val 插入到当前节点的右子树中。递归调用 insertIntoBST 方法，将返回的右子树根节点赋值给 root.right。

 

二、删除二叉树中的节点

题目：

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

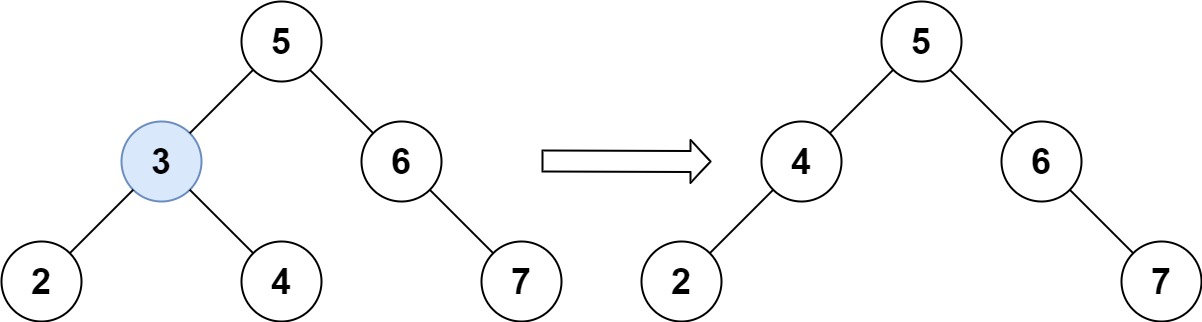
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

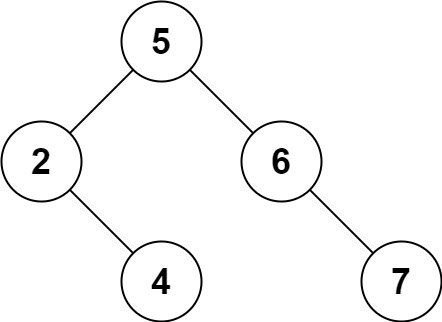
示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

思路：

不但要删除指定节点，还要保持原二叉搜索树的性质不变，总共分为五种情况：

1、节点在树中没有找到，直接返回null

2、节点的左右子树均为空（即要删除的节点为叶子节点）

3、节点的左子树为空，右子树不为空

4、节点的右子树为空，左子树不为空

5、节点的左右子树均不为空，这种情况最为复杂，当要删除的左右子树均存在时，可以将其左或者右节点作为其新的父节点添加到上面。当以右子树节点为新的父节点时，由于二叉搜索树的特性，右子树的值一定比左子树的值大，因此遍历寻找右子树中最左端的节点，然后将将要删去的节点的左子树全部放在该节点下，反之，如果以左子树节点为新的父节点，遍历该左子树最右端的子节点，然后将将要删去的节点的右子树节点全部放在该节点下，全部修改完毕后，删除指定节点，将其子节点返回给上一层，最后输出修改后的二叉搜索树。

代码：

public TreeNode deleteNode(TreeNode root, int key) {
    // 如果根节点为空，直接返回null
    if (root == null)
        return null;
    
    // 如果找到要删除的节点
    if (root.val == key) {
        // Case 1: 要删除的节点是叶子节点（没有子节点）
        if (root.left == null && root.right == null) {
            return null; // 直接返回null，相当于删除这个节点
        }
        // Case 2: 要删除的节点只有右子节点
        else if (root.left == null && root.right != null) {
            return root.right; // 返回右子节点，用以替换被删除的节点
        }
        // Case 3: 要删除的节点只有左子节点
        else if (root.left != null && root.right == null) {
            return root.left; // 返回左子节点，用以替换被删除的节点
        }
        // Case 4: 要删除的节点有左右子节点
        else {
            // 找到右子树中最小的节点（后继节点）
            TreeNode cur = root.right;
            //一直向右子树中的最左端遍历，当左节点为null时，此时cur指向的就是值最小的节点
            while (cur.left != null) {
                cur = cur.left;
            }
            // 将要删除的节点的左子树挂在后继节点的左子树上
            cur.left = root.left;
            // 删除指定的节点，并返回后继节点作为新的子树根节点
            root = root.right;
            return root;
        }
    }
    
    // 如果要删除的节点值小于当前节点值，递归地在左子树中删除
    if (key < root.val)
        root.left = deleteNode(root.left, key);
    
    // 如果要删除的节点值大于当前节点值，递归地在右子树中删除
    if (key > root.val)
        root.right = deleteNode(root.right, key);
    
    // 返回更新后的根节点
    return root;
}

• 如果根节点 root 为空，直接返回 null，因为无法在空树中删除节点。
• 当前节点的值等于要删除的值 key 时，进入删除节点的逻辑。
• Case 1: 要删除的节点是叶子节点（没有子节点），直接返回 null。
• Case 2: 要删除的节点只有右子节点，返回右子节点，用它来替换被删除的节点。
• Case 3: 要删除的节点只有左子节点，返回左子节点，用它来替换被删除的节点。
• Case 4: 要删除的节点有左右子节点，找到右子树中最小的节点作为后继节点，将要删除节点的左子树挂在后继节点的左子树上，然后返回右子树作为新的子树根节点。
• 如果要删除的值 key 小于当前节点的值，递归地在左子树中删除。
• 如果要删除的值 key 大于当前节点的值，递归地在右子树中删除。
• 每次递归调用返回更新后的当前节点 root，确保整棵树的结构被正确更新。

三、修建二叉搜索树 

题目：

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

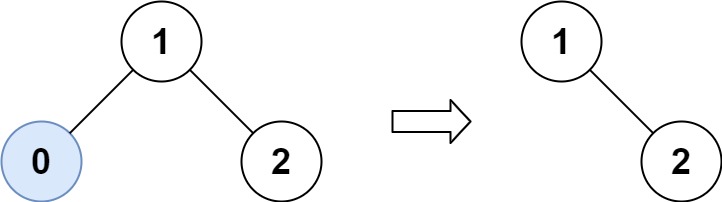
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

示例 2：

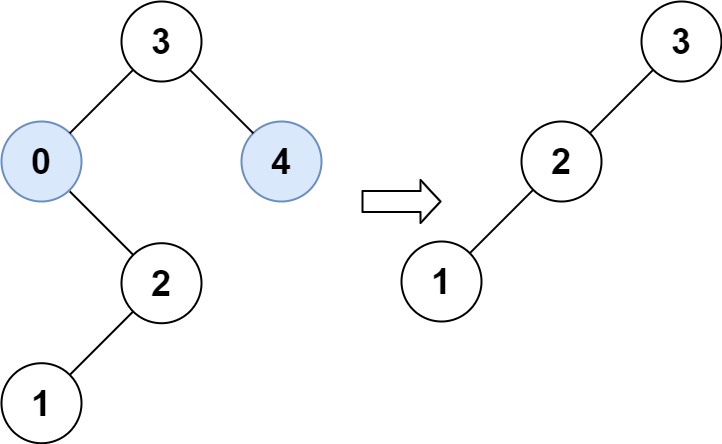
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

思路:

在我们递归操作时，当其左节点小于区间是，其左节点的左节点也不在区间内，但其左节点的右节点有可能存在于区间中，因此需要对右区间额外的进行递归，同理，当右节点大于区间，但是其右节点的左节点有可能在区间中，也需要进行额外的操作

代码：

public TreeNode trimBST(TreeNode root, int low, int high) {
    // 如果根节点为空，直接返回null
    if (root == null) {
        return null;
    }
    
    // 如果当前节点的值小于low，说明当前节点及其左子树都不在范围内，应该修剪右子树
    if (root.val < low) {
        return trimBST(root.right, low, high);
    }
    
    // 如果当前节点的值大于high，说明当前节点及其右子树都不在范围内，应该修剪左子树
    if (root.val > high) {
        return trimBST(root.left, low, high);
    }
    
    // 如果当前节点的值在 [low, high] 范围内，则递归修剪左右子树
    root.left = trimBST(root.left, low, high);
    root.right = trimBST(root.right, low, high);
    
    // 返回修剪后的根节点
    return root;
}

• 如果当前节点的值小于 low：

  • 这意味着当前节点及其左子树的所有节点都不可能在范围 [low, high] 内，因此应该将当前节点及其左子树都丢弃，递归地修剪右子树 root.right。

• 如果当前节点的值大于 high：

  • 类似地，当前节点及其右子树的所有节点都不在范围 [low, high] 内，应该将当前节点及其右子树都丢弃，递归地修剪左子树 root.left。

• 如果当前节点的值在 [low, high] 范围内：

  • 此时，当前节点满足条件，但它的左右子树可能包含不符合范围的节点，因此需要递归地修剪左子树和右子树。

今天的学习就到这里