回来填坑了，本篇推文将详细讲解ALNS算法求解VRP问题及MATLAB代码实现。

算法介绍

节约算法构造初始解

function routes=saving_init(DistMatrix, Demand, Cap)
C_EPS=1e-1;

N=size(DistMatrix,1);
routes=cell(numel(2:N),1);
for i=1:numel(routes)  % 每个节点单独一条路径
    routes{i}=i+1;
end

route_demands=Demand(1:end);
saving=clarke_wright_savings(DistMatrix);  % 计算节约值矩阵

endnode_to_route=[1,1:N-1];

for p=1:size(saving,1)
    i=saving(p,3);
    j=saving(p,4);

    cw_saving = DistMatrix(i,1)+DistMatrix(1,j)-DistMatrix(i,j);
    if cw_saving<0
        break
    end

    left_route = endnode_to_route(i);
    right_route = endnode_to_route(j);

    if isnan(left_route) || isnan(right_route) || left_route==right_route
        continue
    end
    merged_demand = route_demands(left_route)+route_demands(right_route);
    if merged_demand-C_EPS > Cap
        continue
    end
    route_demands(left_route) = merged_demand;

    if routes{left_route}(1)==i
        routes{left_route}=flip(routes{left_route});
    end

    if routes{right_route}(end)==j
        routes{right_route}=flip(routes{right_route});
    end

    if numel(routes{left_route})>1
        endnode_to_route( routes{left_route}(end)) = nan;
    end

    if numel(routes{right_route})>1
        endnode_to_route( routes{right_route}(1)) = nan;
    end

    endnode_to_route( routes{right_route}(end) ) = left_route;
    routes{left_route}=[routes{left_route},routes{right_route}];
    routes{right_route} = nan;
end

routes(cellfun(@(routes) any(isnan(routes)),routes)) = [];

移除算子

1、随机移除算子

function [removed,remove_vc] = RandomRemove(currentSol,dist,toRemove)

%% Remove
cusnum=size(dist,1)-1;
visit=ceil(rand*cusnum);    %随机从所有顾客中随机选出一个顾客
inplan=1:cusnum;            %所有顾客的集合
inplan(inplan==visit)=[];   %将被移出的顾客从原有顾客集合中移出
removed=[visit];            %被移出的顾客集合

while length(removed)<toRemove
    nip=length(inplan);             %原来顾客集合中顾客的数量
    vc=inplan(ceil(rand*nip));      %从inplan数组中选择一个客户
    removed=[removed vc];           %向被移出的顾客集合中添加被移出的顾客
    inplan(inplan==vc)=[];          %将被移出的顾客从原有顾客集合中移出
end
remove_vc=currentSol;               %移出removed中的顾客后的current_vc
nre=length(removed);                %最终被移出顾客的总数量
NV=size(currentSol,1);              %所用车辆数
for i=1:NV
    route=currentSol{i};
    for j=1:nre
        findri=find(route==removed(j),1,'first');
        if ~isempty(findri)
            route(route==removed(j))=[];
        end
    end
    remove_vc{i}=route;
end

[ remove_vc] = deal_vehicles_customer( remove_vc );
end

修复算子

贪婪插入算子

function [newRoutes] = GreedyInsert(removed,removeSol,dist,demands,cap)

while ~isempty(removed)
    %% 将最小插入目标距离增量最小的元素找出来
    [InsertCustomer,InsertVehicle,InsertPosition]=shortestINS(removed,removeSol,dist,demands,cap);
    removed(removed==InsertCustomer)=[];
    %% 根据插入点将元素插回到原始解中
    [removeSol]=insert(InsertCustomer,InsertVehicle,InsertPosition,removeSol);
end
[ newRoutes ] = deal_vehicles_customer(removeSol);
end

输出路径结果

function PlotSolution(model,FinalRoutes)

numRoutes=numel(FinalRoutes);

xCoords=model.x;
yCoords=model.y;
xCoords_depot=xCoords(1);
yCoords_depot=yCoords(1);

Colors=hsv(numRoutes*1);

for j=1:numRoutes
    
    if isempty(FinalRoutes{j})
        continue;
    end
    
    X=[xCoords_depot xCoords(FinalRoutes{j}(2:end-1)) xCoords_depot];
    Y=[yCoords_depot yCoords(FinalRoutes{j}(2:end-1)) yCoords_depot];
    
    Color=1*Colors(j,:);
    
    plot(X,Y,'-o',...
        'Color',Color,...
        'LineWidth',2,...
        'MarkerSize',10,...
        'MarkerFaceColor',Color);
    hold on;
     
end

    plot(xCoords_depot,yCoords_depot,'ks',...
    'LineWidth',2,...
    'MarkerSize',15,...
    'MarkerFaceColor','yellow');
    hold on;

for i=2:numel(xCoords)
    text(xCoords(i)-.5,yCoords(i)+2,num2str(i));
end
end

结果展示

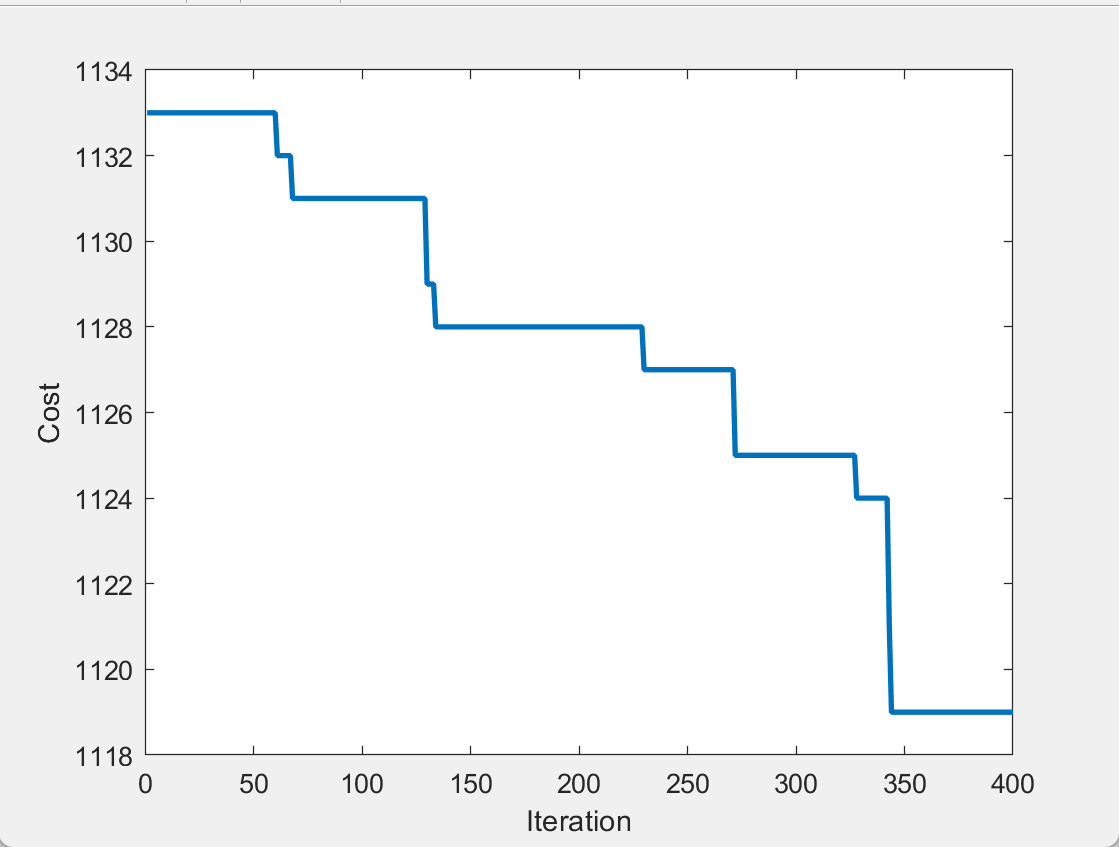
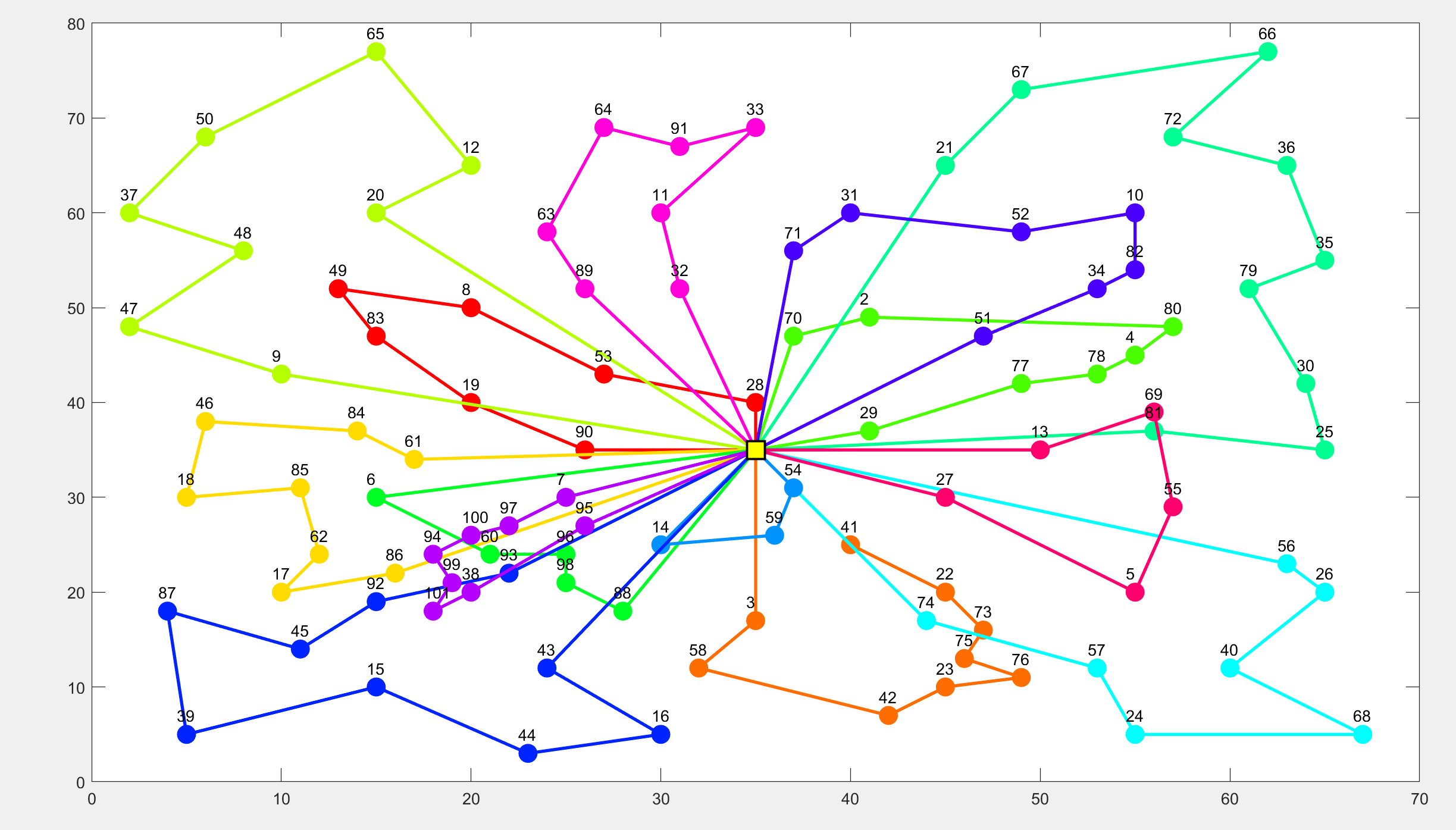
参考文献

PISINGER D, ROPKE S. A general heuristic for vehicle routing problems [J]. Computers & Operations Research, 2007, 34(8): 2403-2435.

ROPKE S, PISINGER D. An adaptive large neighborhood search heuristic for the pickup and delivery problem with time windows [J]. Transportation Science, 2006, 40(4): 455-472.

若有运筹优化建模及算法定制需求，欢迎联系我们私聊沟通