数据结构第二讲:顺序表
- 1.线性表
- 2.什么是顺序表
- 3. 静态顺序表
- 4.动态顺序表
- 4.1顺序表基础
- 4.2顺序表的初始化
- 4.3顺序表的销毁
- 4.4顺序表的尾插
- 4.5顺序表的头插
- 4.6顺序表的尾删
- 4.7顺序表的头删
- 4.8顺序表在指定位置之前插入数据
- 4.9顺序表删除指定位置的数据
- 4.10顺序表查找数据
- 4.11顺序表的打印
- 5.算法题1
- 6.算法题2
- 7.算法题3
- 8.顺序表问题以及思考
1.线性表
顺序表是数据结构中的一种组织方式,是N个具有相同特性数据元素的有限序列,常见的线性表有:顺序表、链表、栈、队列、字符串…
本篇博客我们将详细阐述顺序表的实现以及注意事项
线性表在逻辑上是线性的,在物理结构上不一定是连续的
而顺序表在逻辑上和物理结构上都是连续的
2.什么是顺序表
顺序表是用一段物理地址连续的存储单元存储数据元素的线性结构,一般情况下采用数组存储
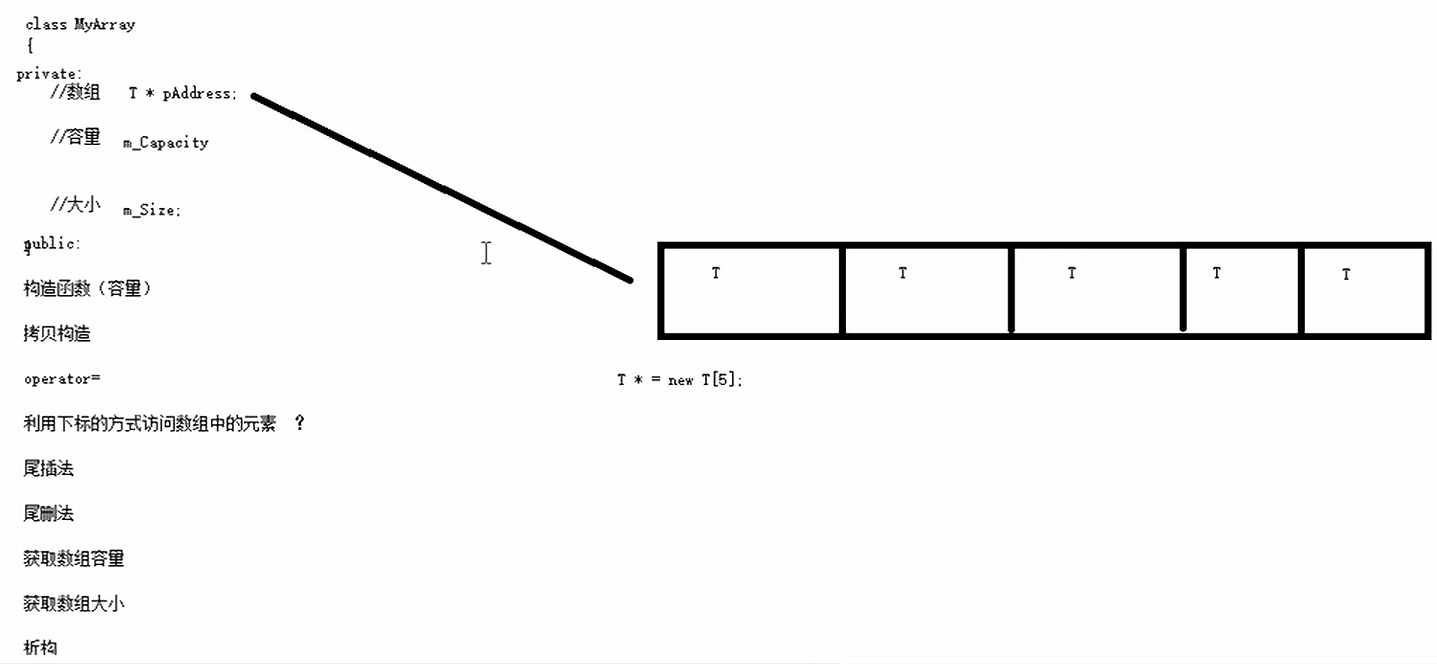
顺序表的底层逻辑是数组,但是有不同于数组,顺序表是对数组进行封装,实现了常见的增删改查的接口,就像这样:

3. 静态顺序表
顺序表分为静态顺序表和动态顺序表两种,静态顺序表的实现如下:
//静态顺序表的实现
typedef int SLDateType;
#define N 100//数组长度
struct Seqlist
{
SLDateType arr[N];//定长数组,用来存储数据
int size;//有效数据个数
};
可以看出,静态顺序表中使用的是定长数组,它的大小是固定的,而动态属性表的大小是可变的,由此可见,动态顺序表要比静态顺序表好用一些
4.动态顺序表
4.1顺序表基础
完成顺序表之前,我们要先实现一个框架,这个框架由结构体来实现,具体如下:
//动态顺序表
typedef int SLDateType;
typedef struct SeqList
{
SLDateType* a;//首先创建一个指针,指向动态开辟的地址
int size;//有效数据的个数
int capacity;//空间容量
}SL;
我们通过这个结构体创建了一个 sl 结构体变量
4.2顺序表的初始化
创建了一个变量,首先要做的就是对它的初始化,初始化很简单,操作如下:
//顺序表的初始化
void SLInit(SL* pa)
{
//先将指向的空间赋值为0
pa->a = NULL;
//将大小全部初始化为0
pa->capacity = 0;
pa->size = 0;
}
4.3顺序表的销毁
写出了顺序表的初始化,我们顺便将顺序表的销毁也一并写了就行了,方式如下:
//顺序表的销毁
void SLDestory(SL* pa)
{
//将结构体中的变量一一销毁即可
if (pa->a != NULL)
{
free(pa->a);
pa->a = NULL;
}
pa->capacity = 0;
pa->size = 0;
}
4.4顺序表的尾插

既然size指向的位置就是需要插入的位置的下表,那么我们直接在size这个位置插入数据,然后将size++,指向下一个位置即可,操作方法如下:
//顺序表尾插
void SLPushBack(SL* ps, SLDateType x)
{
if (ps->capacity == ps->size)
{
//首先判断一开始是否有空间
int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
//然后需要开辟空间,才能插入数据
SLDateType* pa = (SLDateType*)realloc(ps->a, newcapacity * sizeof(SLDateType));//此时一般开辟两倍的空间
if (pa == NULL)
{
perror("realloc faile!");
exit(-1);
}
ps->a = pa;
ps->capacity = newcapacity;
}
//尾插就是直接将数据插入即可
ps->a[ps->size++] = x;
}
在这串代码中,对于空间大小的判断需要经常使用,所以我们将它封装成一个函数即可:
//顺序表检查空间是否充足
void SLCheckCapacity(SL* ps)
{
if (ps->capacity == ps->size)
{
//首先判断一开始是否有空间
int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
//然后需要开辟空间,才能插入数据
SLDateType* pa = (SLDateType*)realloc(ps->a, newcapacity * sizeof(SLDateType));//此时一般开辟两倍的空间
if (pa == NULL)
{
perror("realloc faile!");
exit(-1);
}
ps->a = pa;
ps->capacity = newcapacity;
}
}
这时尾插就变得非常朴实无华了:
//顺序表尾插
void SLPushBack(SL* ps, SLDateType x)
{
assert(ps);
SLCheckCapacity(ps);
//尾插就是直接将数据插入即可
ps->a[ps->size++] = x;
}
4.5顺序表的头插
有尾插,那肯定要有头插,头插就是将所有数据向后移,然后在下标为0的位置插入数据即可:
平移前:

平移之后:

实现方法如下,一个简单的for循环即可:
//顺序表的头插
void SLPushFront(SL* ps, SLDateType x)
{
//注意点:头插之前,需要判断ps是否为空
assert(ps);
//头插也一样,也需要先判断一下空间是否充足
SLCheckCapacity(ps);
//头插首先需要将所有数据进行后移
for (int i = ps->size; i > 0; i--)
{
ps->a[i] = ps->a[i - 1];
}
//随后将数据插入到第一位即可
ps->a[0] = x;
ps->size++;
}
4.6顺序表的尾删
尾删非常简单,将size–就行了,因为根本就没有必要将数据删除!!!方法如下:
//顺序表的尾删
void SLPopBack(SL* ps)
{
//首先需要先判断ps是否为空,没有空间不能删除,指针为空不能删除
assert(ps);
assert(ps->size);
//直接将size-1就行了
ps->size--;
}
4.7顺序表的头删
头删也很简单,将所有数据向前平移即可,将第一个数据覆盖掉就行了:
//顺序表的头删
void SLPopFront(SL* ps)
{
//头删时,空指针不能删,没有空间不能删
assert(ps);
assert(ps->size);
//头删将所有的数据向前平移,size--即可
for (int i = 0; i < ps->size-1; i++)
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}
4.8顺序表在指定位置之前插入数据
随机插入数据才更显得高级,难道不是吗?
假设pos是我们需要插入位置的下标,方法根据画图来理解吧:


实现方法如下:
//顺序表在指定位置之前插入数据
void SLInsert(SL* ps, SLDateType x, int pos)
{
//我们插入的位置肯定不能够超过有效空间的位置,也不能小于0
assert(ps);
assert(pos >= 0 && pos <= ps->size);
//先检查空间是否足够
SLCheckCapacity(ps);
//插入就是将数据进行后移,空出位置进行插入即可
for (int i = ps->size; i > pos; i--)
{
ps->a[i] = ps->a[i - 1];
}
ps->a[pos] = x;
ps->size++;
}
4.9顺序表删除指定位置的数据
要删除指定位置的数据的话只需要一个平移就可以了,就是这样:

实现方法如下:
//顺序表删除指定位置的数据
void Erase(SL* ps, int pos)
{
assert(ps);
assert(pos >= 0 && pos < ps->size);
for (int i = pos; i < ps->size - 1; i++)
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}
4.10顺序表查找数据
查找数据十分简单,只需要遍历数组就可以了:
//顺序表查找数据
void SLFind(SL* ps, SLDateType x)
{
assert(ps);
for (int i = 0; i < ps->size; i++)
{
if (ps->a[i] == x)
{
printf("找到了! 下标为:%d\n", i);
return;
}
}
printf("没找到!\n");
}
4.11顺序表的打印
实现了那么多的操作,不打印一下看一下那怎么能行呢?打印很简单,方法如下:
//打印顺序表
void SLPrint(SL *ps)
{
for (int i = 0; i < ps->size; i++)
printf("%d ", ps->a[i]);
printf("\n");
}
5.算法题1
链接: 移除元素
int removeElement(int* nums, int numsSize, int val) {
int src = 0;
int dst = 0;
int k = numsSize;
while (src < numsSize) {
if (nums[src] == val) {
src++;
k--;
} else
nums[dst++] = nums[src++];
}
return k;
}
6.算法题2
链接: 删除有序数组中的重复项
int removeDuplicates(int* nums, int numsSize) {
int src = 1;
int dst = 0;
int k = 1;
while (src < numsSize) {
if (nums[src] != nums[dst]) {
nums[++dst] = nums[src];
k++;
}
src++;
}
return k;
}
7.算法题3
链接: 合并两个有序数组
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
int l1 = m - 1;
int l2 = n - 1;
int l3 = nums1Size - 1;
while (1) {
if (l3 == l1)
return;
if (l3 == l2)
break;
if (nums1[l1] > nums2[l2]) {
nums1[l3--] = nums1[l1--];
} else {
nums1[l3--] = nums2[l2--];
}
}
for (int i = l2; i >= 0; i--)
nums1[i] = nums2[i];
}
8.顺序表问题以及思考
当然,顺序表并不是完美的,它仍然具有着一些问题:

为了解决以上问题,我们就需要引入一个东西:链表,这个我们下一次再讲!!!