847. 访问所有节点的最短路径

存在一个由 n 个节点组成的无向连通图，图中的节点按从 0 到 n - 1 编号。

给你一个数组 graph 表示这个图。其中，graph[i] 是一个列表，由所有与节点 i 直接相连的节点组成。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

示例 1：

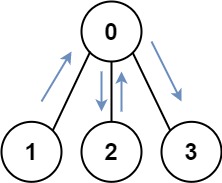
**输入：**graph = [[1,2,3],[0],[0],[0]]
**输出：**4
**解释：**一种可能的路径为 [1,0,2,0,3]

示例 2：

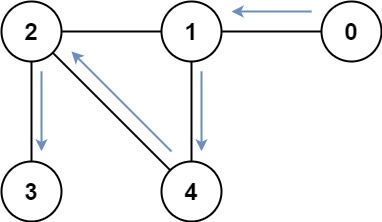
**输入：**graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
**输出：**4
**解释：**一种可能的路径为 [0,1,4,2,3]

提示：

• n == graph.length
• 1 <= n <= 12
• 0 <= graph[i].length < n
• graph[i] 不包含 i
• 如果 graph[a] 包含 b ，那么 graph[b] 也包含 a
• 输入的图总是连通图

这个题目就和我们狄克斯特拉算法标记vis还是有区别的，我们的节点可以重复访问，我们不能对节点进行标记

class Solution {
public:
    int shortestPathLength(vector<vector<int>>& graph) {
        int n = graph.size();
        queue<tuple<int, int, int>> q;
        vector<vector<bool>> vis(n, vector<bool>(1 << n));
        // 那么从哪一个点开始呢，其实我们采用bfs我们可以把所有的点都先入队列
        for (int i = 0; i < n; i++) {
            q.push({ i,1 << i,0 });
            vis[i][1 << i];
        }
        while (q.size()) {
            auto [u,now,step] = q.front(); q.pop();
            if (now == ((1 << n) - 1)) return step;
            for (auto v : graph[u]) {
                int a = (1 << v) | now;
                if (vis[v][a]) continue;  // 注意这个是v
                vis[v][a] = 1;
                q.push({ v,a,step + 1 });
            }
        }
        return -1;
    }
};