一、选择

以下选项中，对Java关于内存回收的说法正确的是（）

A 程序员必须创建一个线程来释放内存
B 内存回收程序负责释放无用内存
C 内存回收程序允许程序员直接释放内存
D 内存回收程序可以在指定的时间释放内存对象

Test.main() 函数执行后的输出是（）

class Test {
    public static void main(String[] args) {
        System.out.println(new B().getValue());
    }
    static class A {
        protected int value;
        public A (int v) {
            setValue(v);
        }
        public void setValue(int value) {
            this.value= value;
        }
        public int getValue() {
            try {
                value ++;
                return value;
            } finally {
                this.setValue(value);
                System.out.println(value);
            }
        }
    }
    static class B extends A {
        public B () {
            super(5);
            setValue(getValue()- 3);
        }
        public void setValue(int value) {
            super.setValue(2 * value);
        }
    }
}

JUnit主要用来完成什么（）

A 发送HTTP请求
B 建立TCP连接
C 集成测试
D 单元测试

二、编程（比较简单）

1. 两种排序方法

两种排序方法

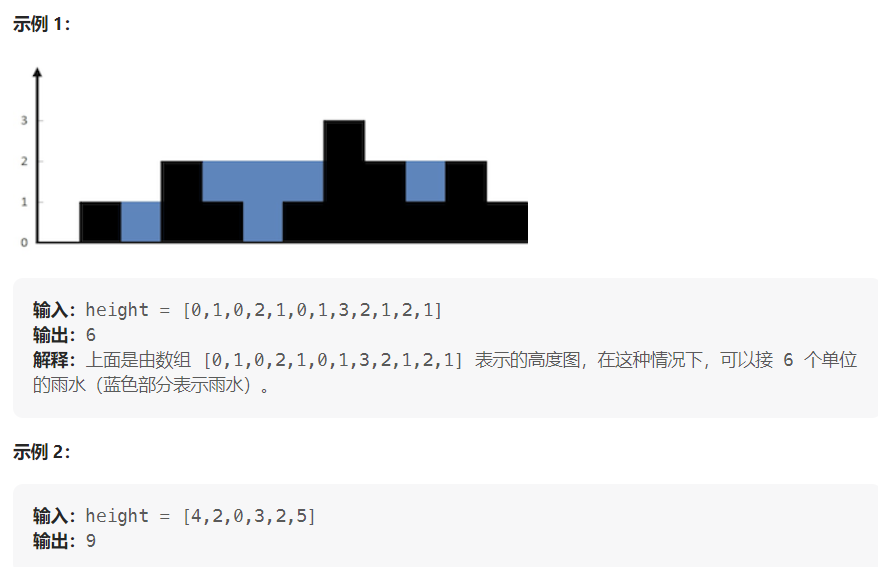
考拉有n个字符串，任意两个字符串长度都是不同的。考拉最近学习到有两种字符串的排序方法： 1.根据字符串的字典序排序，2.根据字符串的长度排序。
考拉想知道自己的这些字符串排列顺序是否满足这两种排序方法，考拉要忙着吃树叶，所以需要你来帮忙验证。
输出：字典序"lexicographically"，字符串长度出"lengths"，两种"both"，否则"none"。

2. 求最小公倍数（主要注意辗转相除法就行）

最小公倍数

正整数A和正整数B 的最小公倍数是指能被A和B整除的最小的正整数值，设计一个算法，求输入A和B的最小公倍数。

答案

1. 选择

① 垃圾回收程序是一般是在堆上分配空间不够的时候会自己进行一次GC，程序员不需要也不能主动释放内存
② Java的内存释放由垃圾回收程序来进行释放
③ 在Java里，内存的释放由垃圾回收程序进行管理，程序员不能直接进行释放
④ 程序员可以调用System.gc()运行垃圾回收器，但是不能指定时间

故：选B

★ 本题的关键是对于java多态的理解：调用的是实例化子类中重写的方法，只有明确调用了super.xxx关键词或者是子类中没有该方法时，才会去调用父类相同的同名方法。
[注意：即使是子类调用父类的构造方法，并且有同名函数的时候，也是调用子类的函数]

① new B 是实例化B对象，针对的是B类，所以此时直接看B类，发现B类是继承于A类的。B的构造方法中super(5)显式调用了A的构造方法；此时去看A的构造方法，发现A的构造方法是setValue方法，并且该方法在子类B中也是存在的。且此刻正在初始化的对象是B的一个实例，因此这里调用的实际是B类的setValue方法，于是调用B类中的setValue方法 == > 而B类中setValue方法显示调用父类的setValue方法，将B实例的value值设置为2 x 5 = 10；
② 然后B类中接着往下走，setValue(getValue() - 3);此时针对的都是B实例化的对象，如果B中有就直接调用B中的方法即可，没有的话调用父类的方法：B中有setValue可以直接调用，但是没有getValue则去调用A类中的该方法。
③ 调用A类中的getValue：首先value++，即value=10+1，此时由于return而进行暂存；接着往下走到了finally，此时调用this.setValue(value)即调用的是 B类中的方法（一定要注意this是指当前对象，而当前对象是B实例化的对象，所以是调用B类中的setValue方法！！），即：super.setValue(2value)，即super.setValue(211)，然后又调用父类的setValue，则此时value=22，并打印出22。
④ 然后再调用setValue，直接在B中调用就行，而(getValue-3)中的getValue其实就是finally结束之后进行返回的value值，也就是在try中就已经暂存好的值，即11，所以此时(getValue-3)=11-3=8；然后super.setValue(2*8)，即 此时value=16 。
⑤ 到这里new B完结，然后new B.getValue(); 调用的getValue方法只能是父类A中的，因为子类B中没有该方法，此时value=17并进行暂存，然后执行finally：this.setValue()调用的还是B中的方法，即setValue(2*17)，此时打印34。
⑥ 执行完finally之后返回的value是之前暂存的17，并且打印。
⑦ 所以：最后执行的结果是：22 34 17

故：选D

① JUnit 是一个 Java 语言的单元测试框架。它由 Kent Beck 和 Erich Gamma 建立，逐渐成为源于 Kent Beck 的 sUnit 的 xUnit 家族中最为成功的一个。 JUnit 有它自己的 JUnit 扩展生态圈。多数 Java 的开发环境都已经集成了 JUnit 作为单元测试的工具 。
② JUnit 是由 Erich Gamma 和 Kent Beck 编写的一个 回归测试 框架（ regression testing framework ）。 Junit 测试是程序员测试，即所谓 白盒测试 ，因为程序员知道被测试的软件如何（ How ）完成功能和完成什么样（ What ）的功能。 JUnit 是一套框架，继承 TestCase 类，就可以用 JUnit 进行自动测试了。

故：选D

在Java中，数组存储在堆中连续内存空间里
return是终止函数并返回。

2. 编程

两种排序方法

1）思路：
主要注意常用的方法。

将接收的字符串都放到String数组中，利用string的compareTo方法来按ascii比较字符串字典序排序，利用string的length方法来比较字符串的长度排序。

2）代码：

// 两种排序方式：字典序以及长度顺序
// 直接使用compareTo比较字典序，使用length比较长度就行

import java.util.Scanner;

public class Main {
    // 字典顺序
    private static boolean isDirectory(String[] strs) {
        // 前后两个字符串比较就行
        for (int i = 0; i < strs.length-1; i++) {
            if(strs[i].compareTo(strs[i+1]) > 0) {
                // 说明不符合要求
                return false;
            }
        }
        // 来到这儿，循环结束，符合要求
        return true;
    }
    // 长度顺序
    private static boolean isLength(String[] strs) {
        // 前后两个字符串比较就行
        for (int i = 0; i < strs.length-1; i++) {
            if(strs[i].length() > strs[i+1].length()) {
                // 说明不符合要求
                return false;
            }
        }
        // 来到这儿，循环结束，符合要求
        return true;
    }

    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        int n = in.nextInt();
        String[] strs = new String[n];
        for (int i = 0; i < n; i++) {
            strs[i] = in.next();
        }
        // 然后开始进行判断
        if(isDirectory(strs) && isLength(strs)) {
            System.out.println("both");
        } else if(isLength(strs)) {
            System.out.println("lengths");
        } else if(isDirectory(strs)) {
            System.out.println("lexicographically");
        } else {
            System.out.println("none");
        }
    }
}

最小公倍数

1）思路：
① 最小公倍数 = 两数之积 / 最大公约数
② 注意最大公约数求法：辗转相除法
③ 辗转相除法：对于输入的两个数进行连续求余，直到余数为0，求余的分母即为结果。

2）代码：

import java.util.Scanner;

public class Main {
    // 最大公约数
    private static int maxDiv(int m, int n) {
        int c = 1;
        while(n!=0) { //这里c 或n 都ok！
            c = m%n;
            m = n;
            n = c;
        }
        return m;
    }

    // 求最小公倍数
    private static int minMul(int m, int n) {
        int max = maxDiv(m,n);
        // 两个数之乘积 = min*max
        return (m*n/max);
    }
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        while (in.hasNextInt()) {
            int m = in.nextInt();
            int n = in.nextInt();
            int mul = minMul(m,n);
            System.out.println(mul);
        }
    }
}