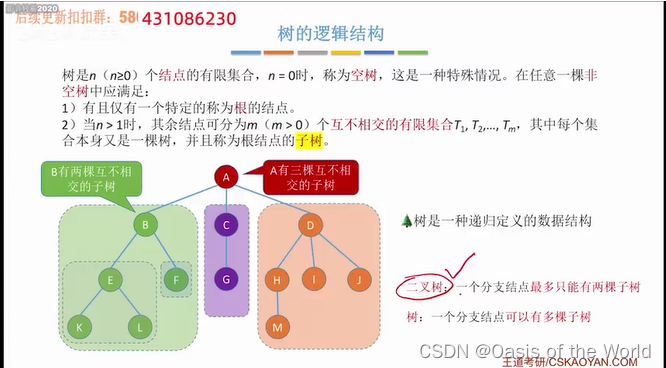
1 树的定义
1.1 树的基本概念
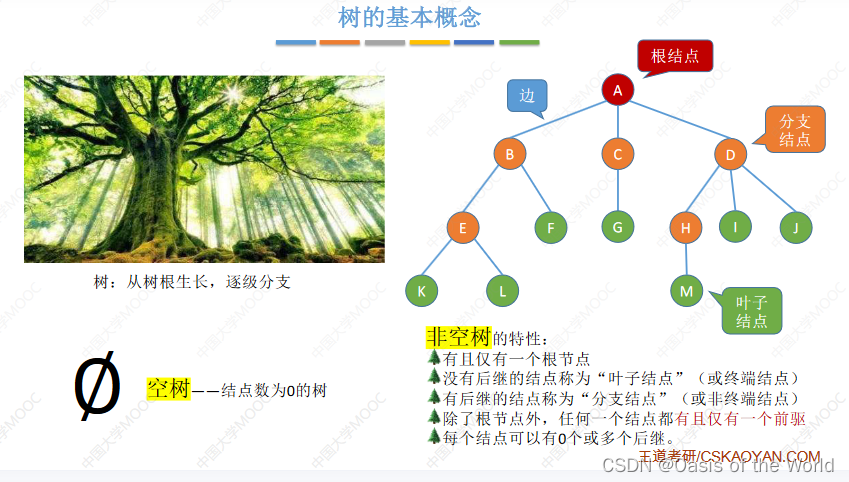
分支可以称为边,结点可以用于存放数据结构。
除了根节点,其他节点只有一个前驱!!!!
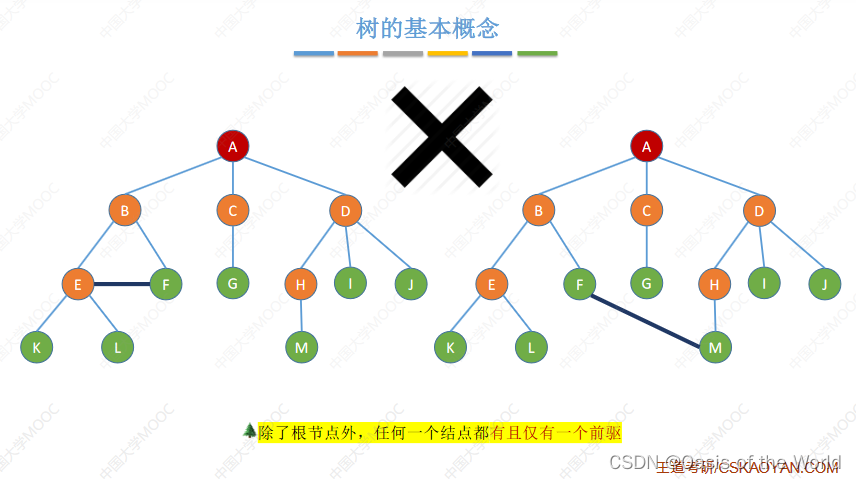
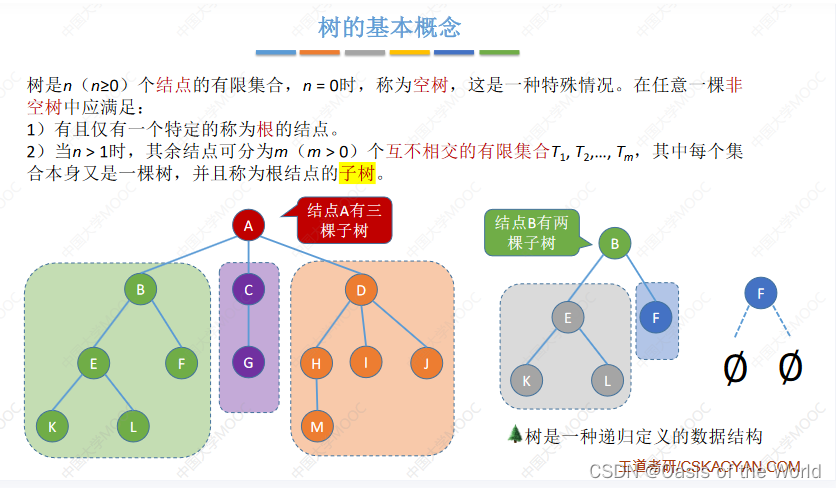
互不相交也就是 只有一个前驱结点!
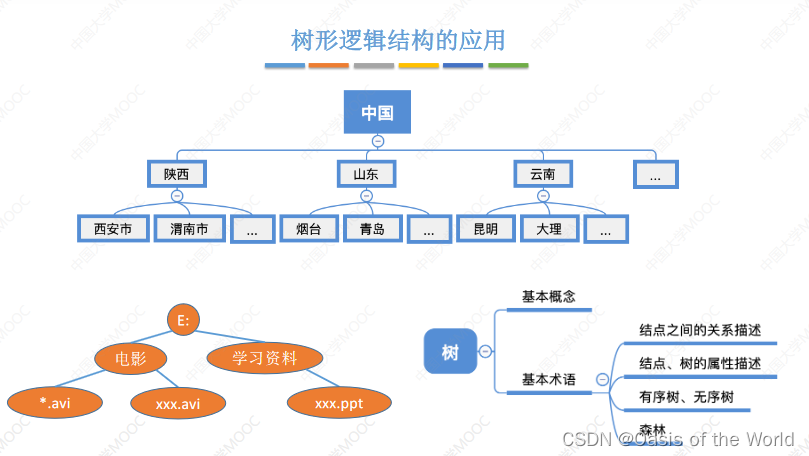
树应用的很广的
1.2 结点之间的关系
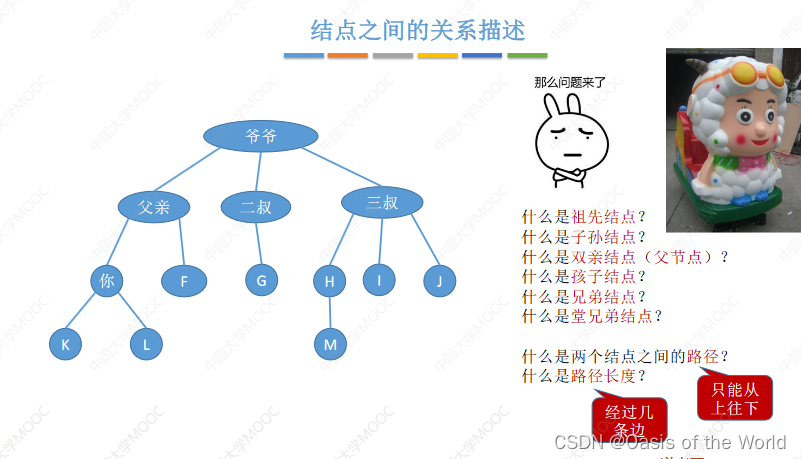
直接前驱是父节点,路径是单向的【只能从上往下走】
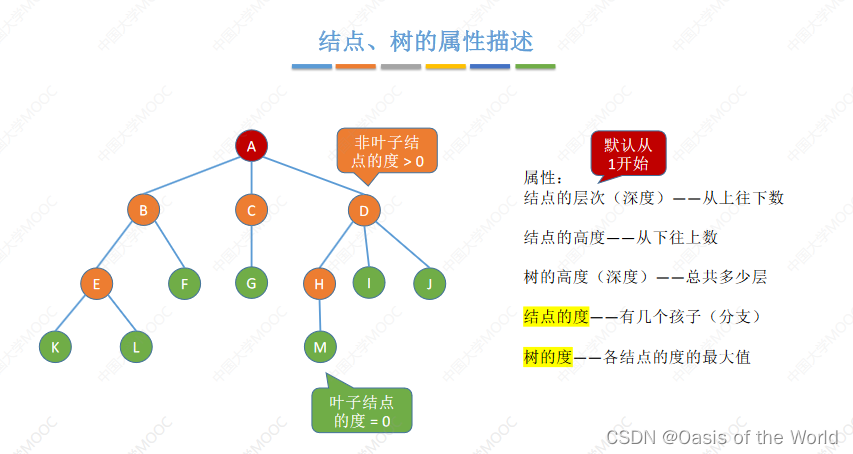
度为0就是叶子结点,度大于0就是非叶子结点!树的度-各结点的最大值!
1.3 有序树和无序数
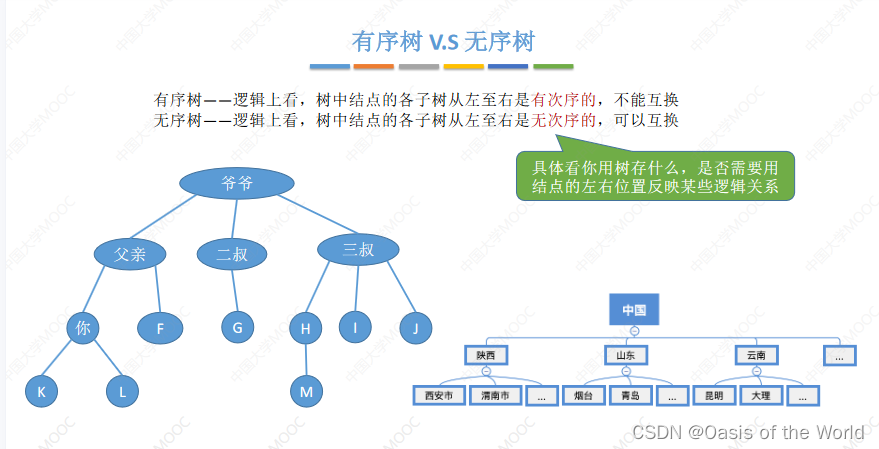
家谱按照出生的顺序
1.4 树和森林
m棵不相交的树
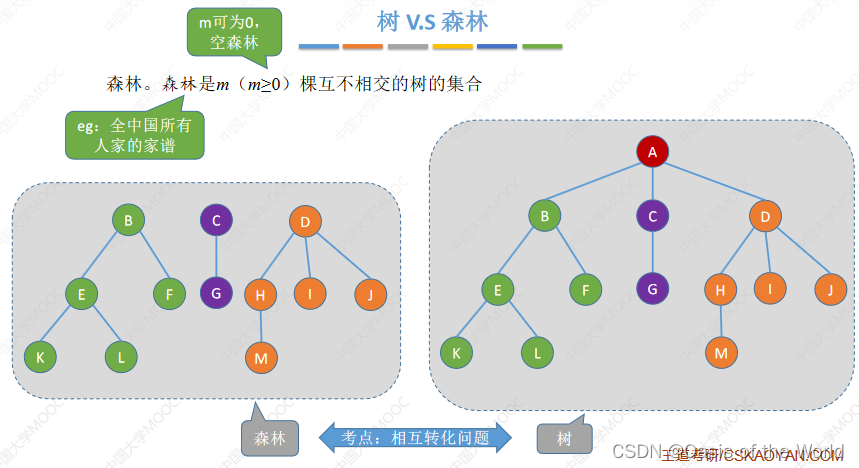
2 树的性质
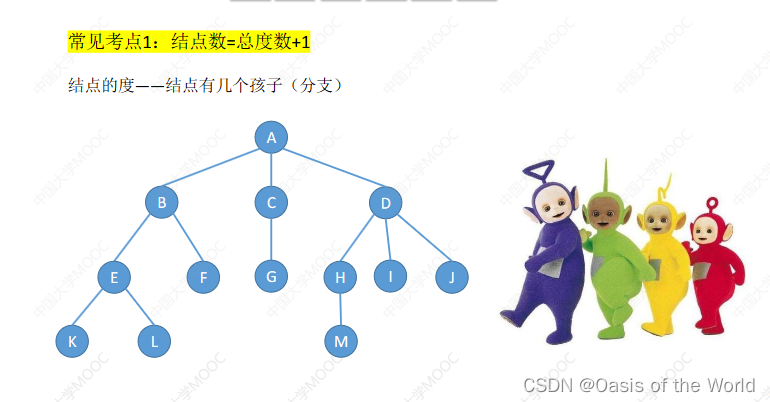
结点数 = 总度数+1
这个1其实就是根结点
度为m的数和m叉树的区别

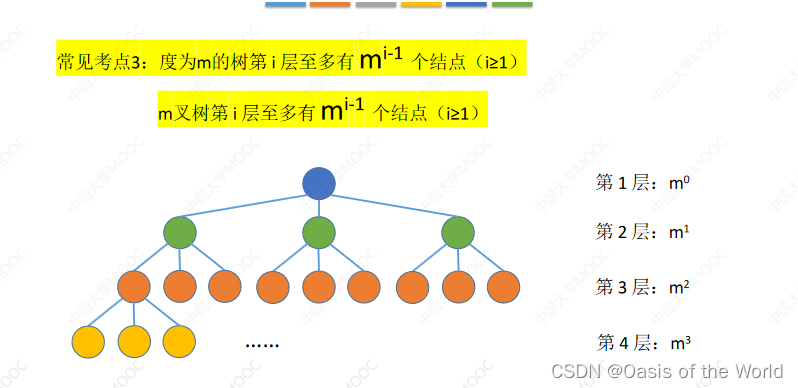
度为m的树最多结点
高度为h的m叉树最多结点
就素等比数列
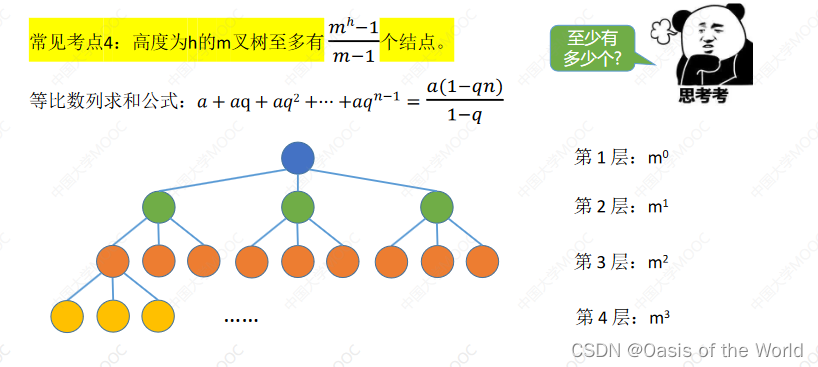
度和叉树

具有n个结点的m叉树的最小高度


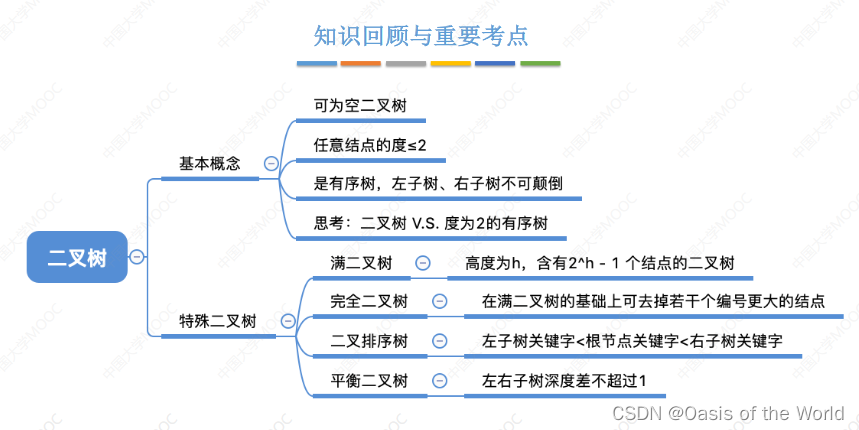
3 二叉树概念【高频】

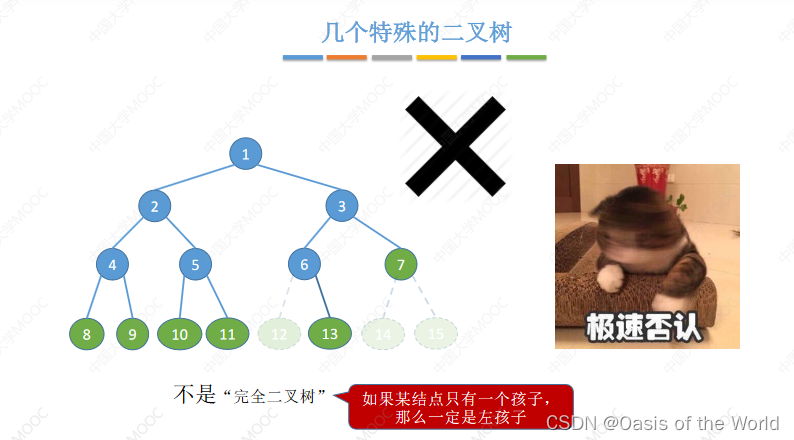
满二叉树 完全二叉树
注意满二叉树的坐标规律!!!!【有利于以后的顺序存储!!】
在满二叉树的基础上去掉序号大的结点!
完全二叉树最多只有一个度为1的结点!!

二叉排序树
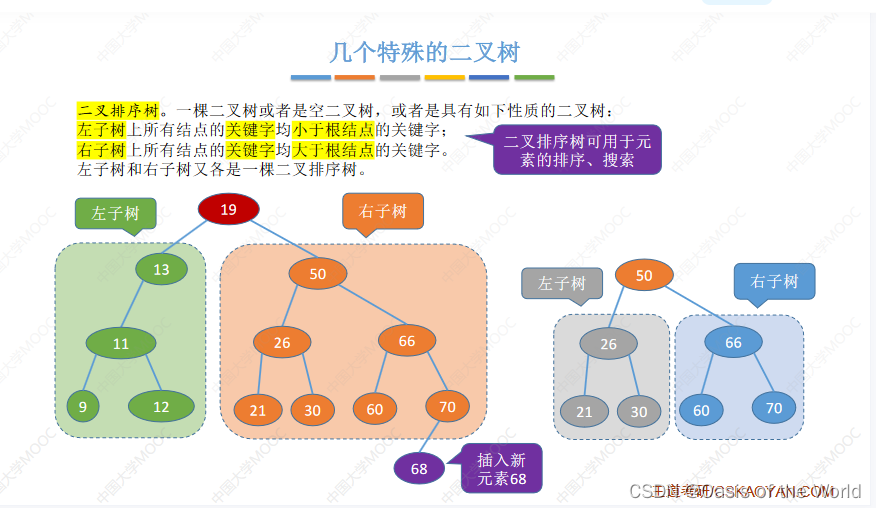
搜索就会简单哦!插入一个元素还可以是二叉排序树。二叉排序树可用于元素的排序、搜索!
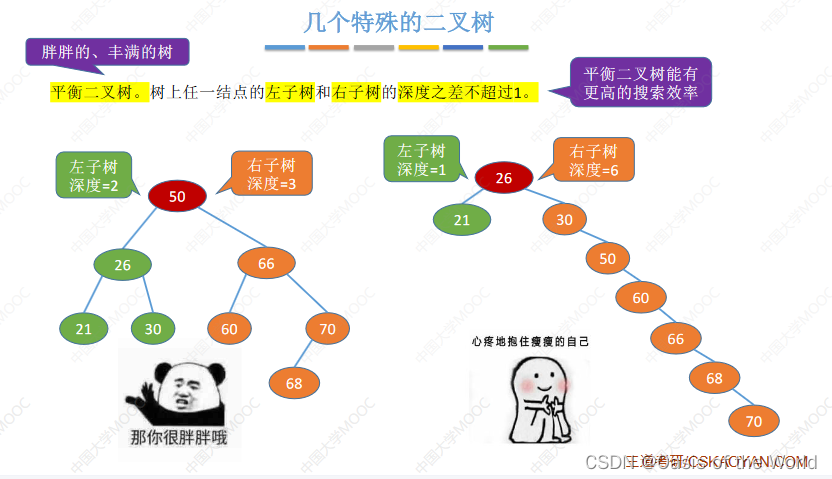
平衡二叉树
更平衡会得到更高效的搜索效率!!!长的越胖越好
4 二叉树的常考性质
4.1 二叉树
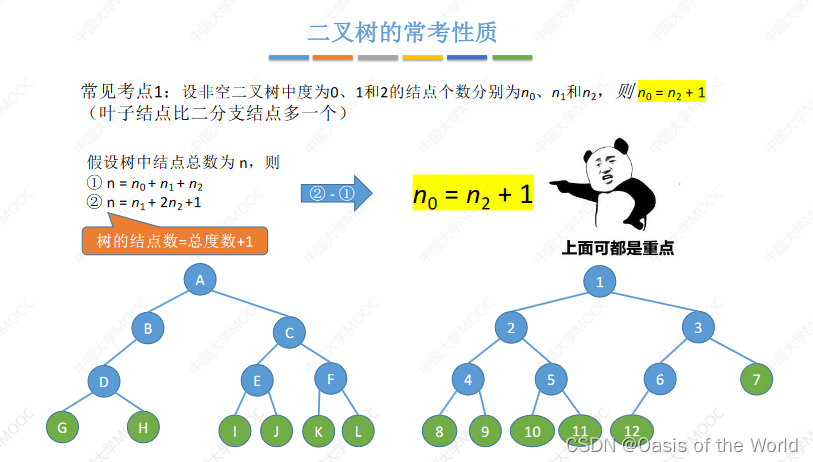
叶子结点的个数 = 二分支结点的个数+1
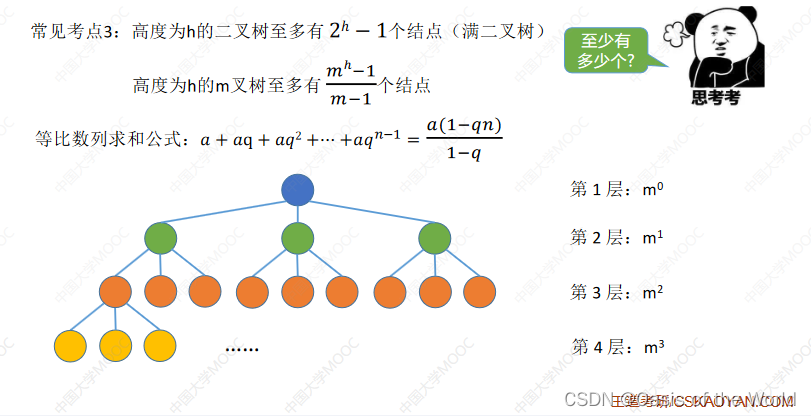
二叉树的第i层最多结点

高度为h的二叉树最多结点
4.2 完全二叉树
结点为n的完全二叉树高度

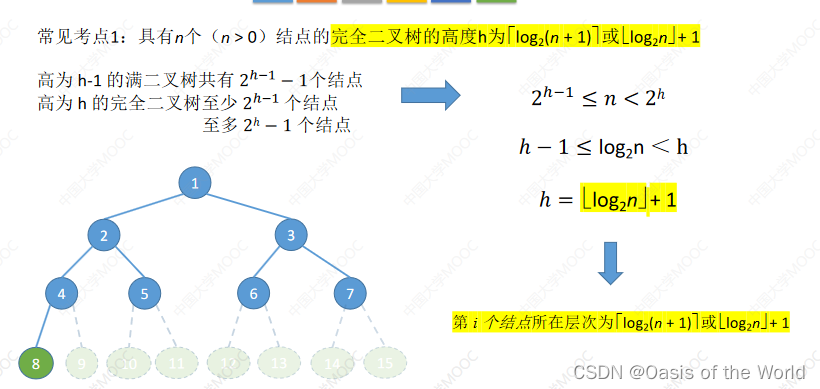
给出总结点推出度为0、1、2的结点个数
n0 = n2+1 则n0+n2 = 2n2 +1 那么意思就是n0+n2一定是奇数

总结

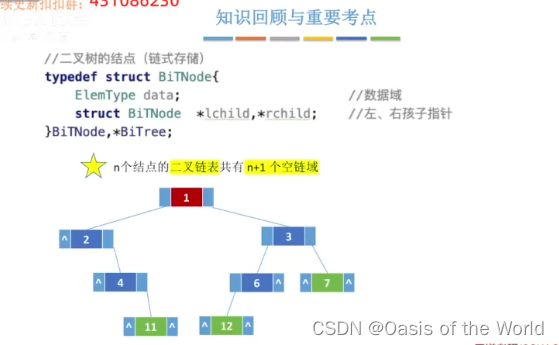
4.3 二叉树的存储结构
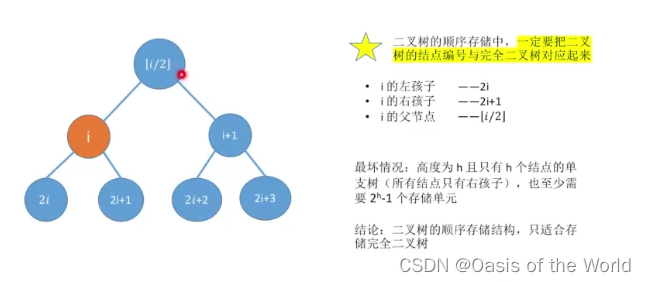
4.3.1 顺序存储
完全二叉树
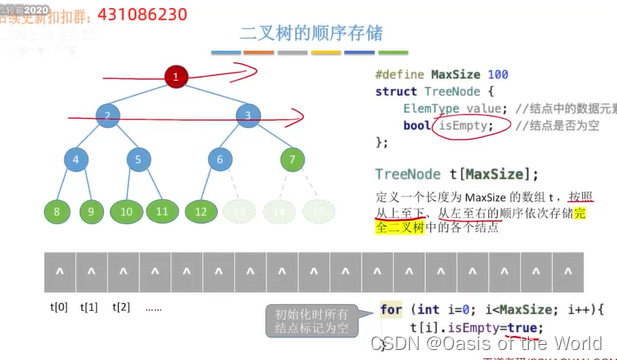
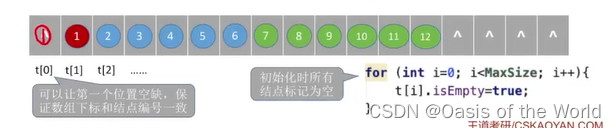


非完全二叉树



4.3.2 链式存储


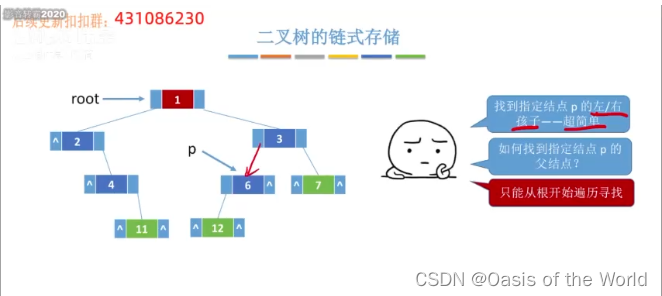

![]()
总结
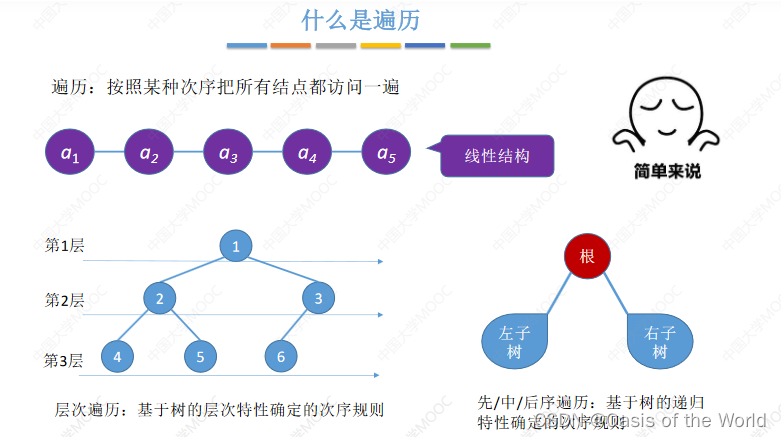
5 二叉树的遍历
5.1 二叉树 先/中/后序遍历

遍历:按照某个次序把所有的结点都访问一下
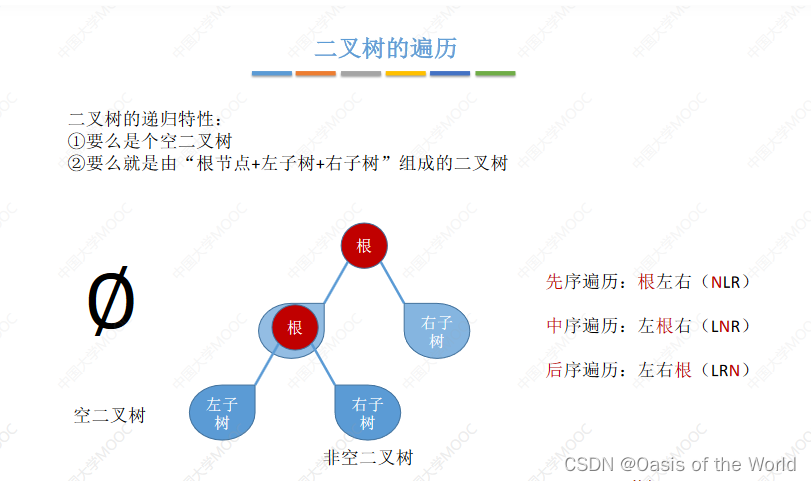
先序遍历也叫做先根遍历!
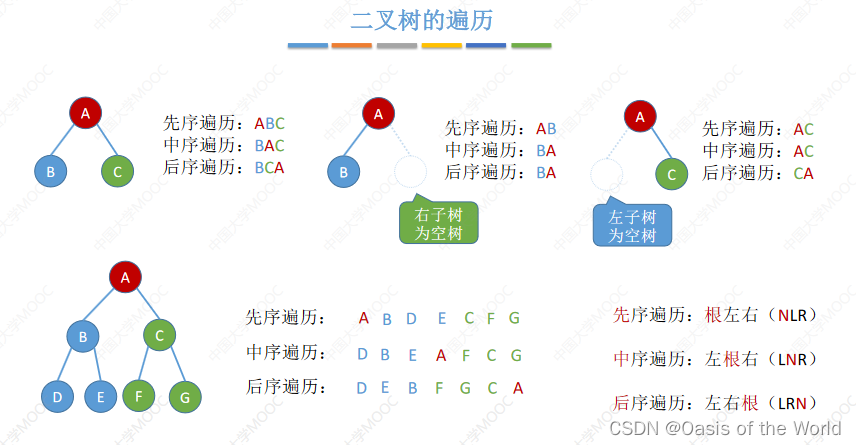
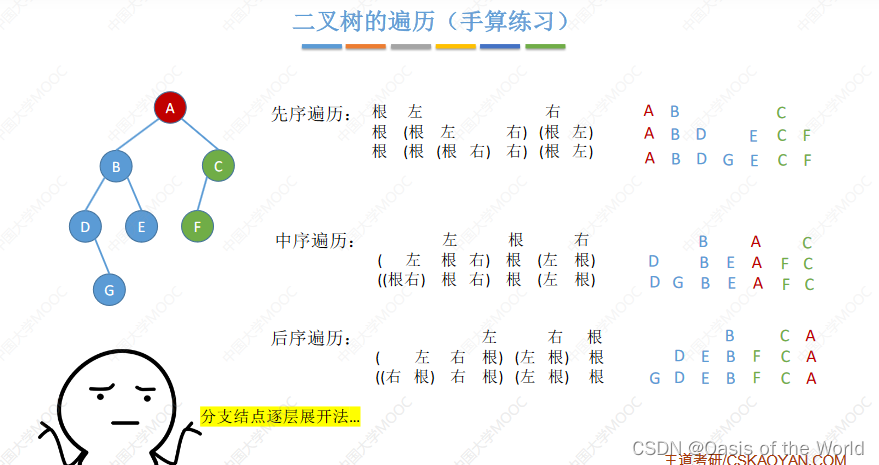
分支结点逐层展开法【写序列】
手算的时候一层一层的写!!!!【分支结点逐层展开法!】
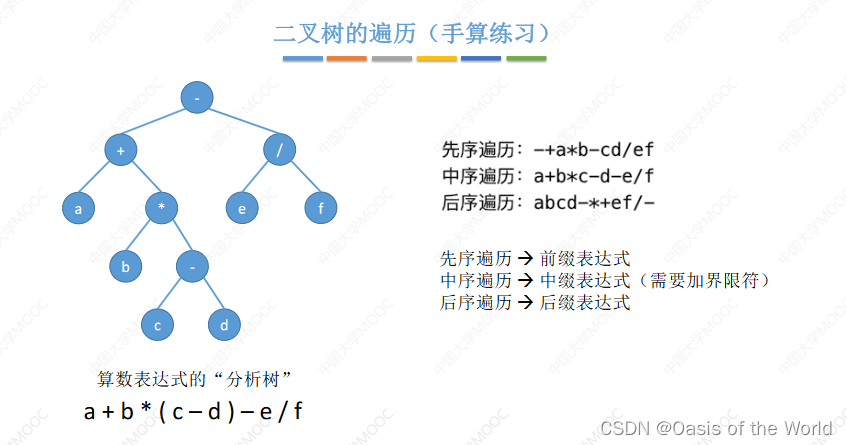
中缀表达式是没有界限符的!!!
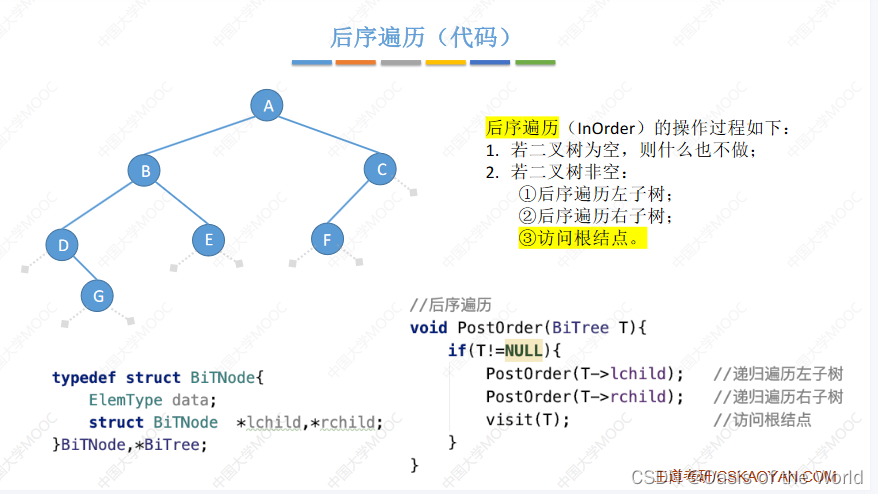
代码
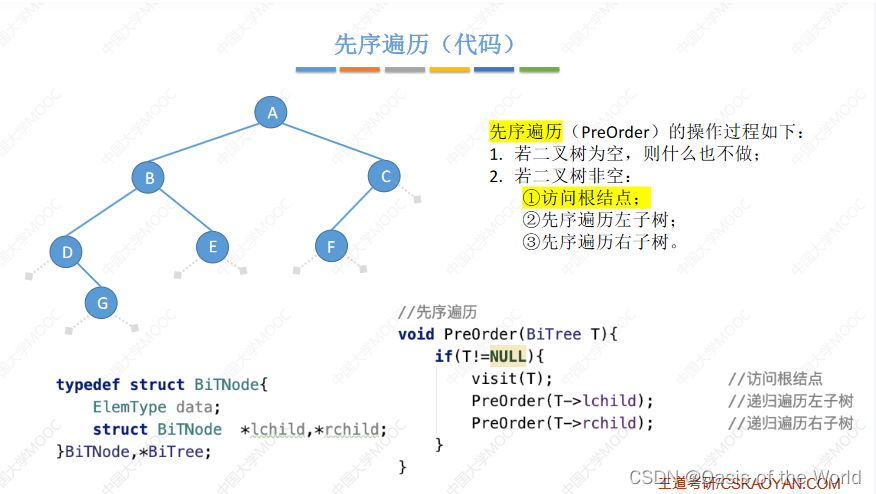

从你的全世界路过法【写序列】
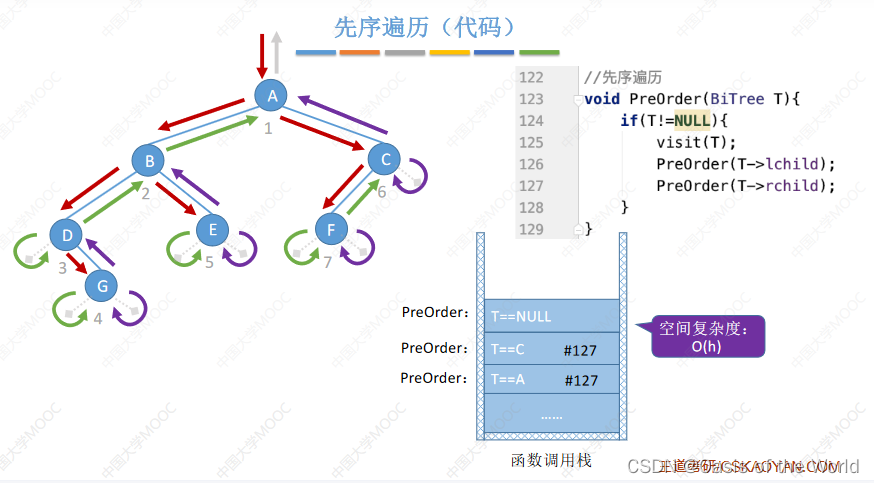
空间复杂度0(h+1)
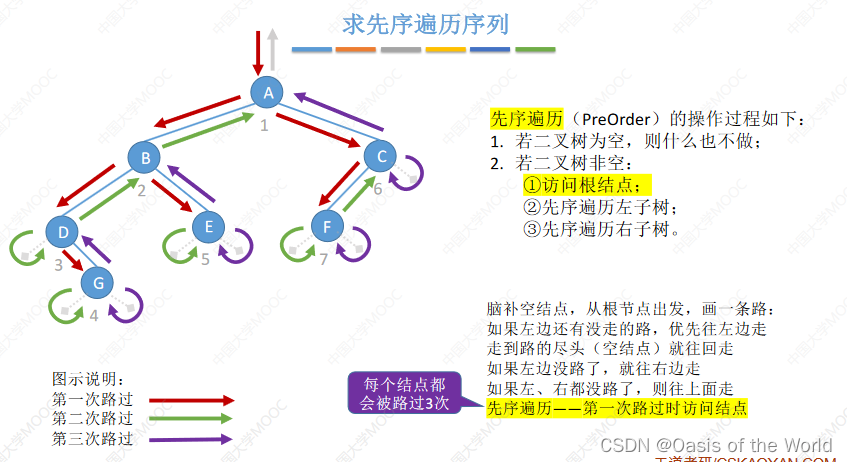
A B D G E C F 第一次路过的时候就访问结点!!!
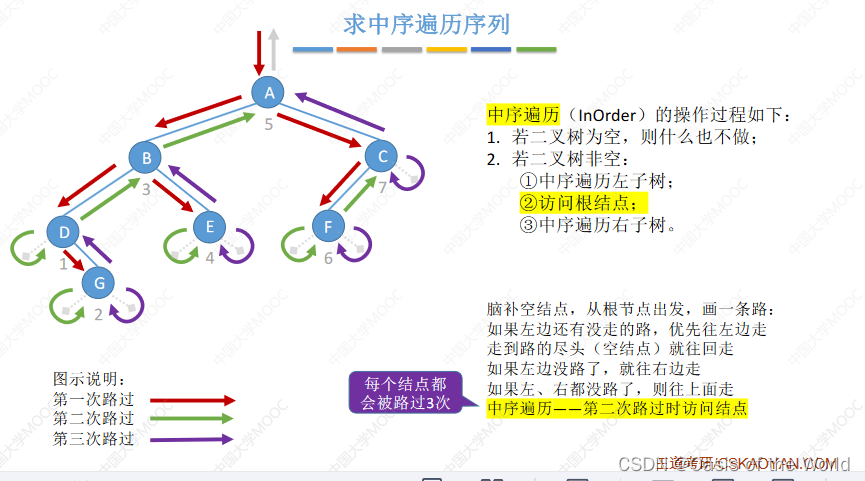
中序:D G B E A F C 第二次路过的时候访问结点
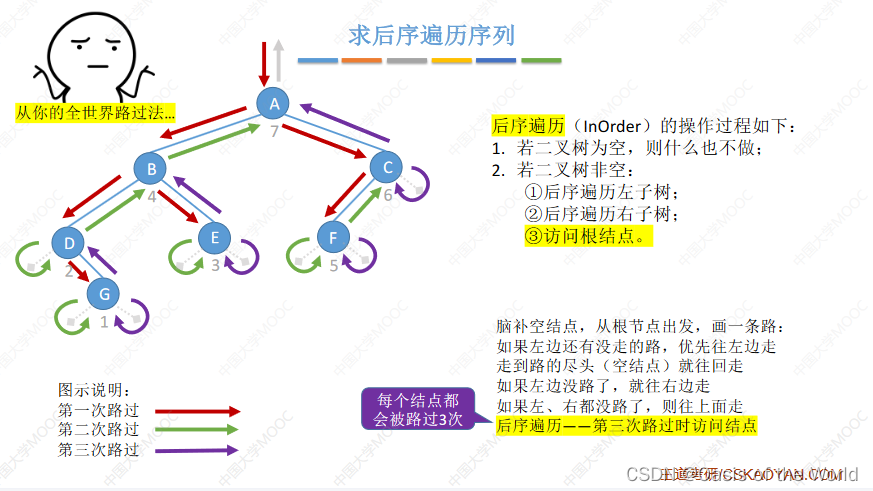
后序:第三次路过的时候

用从你的全世界路过法:就是画出路径你就懂了:【类似这样的】

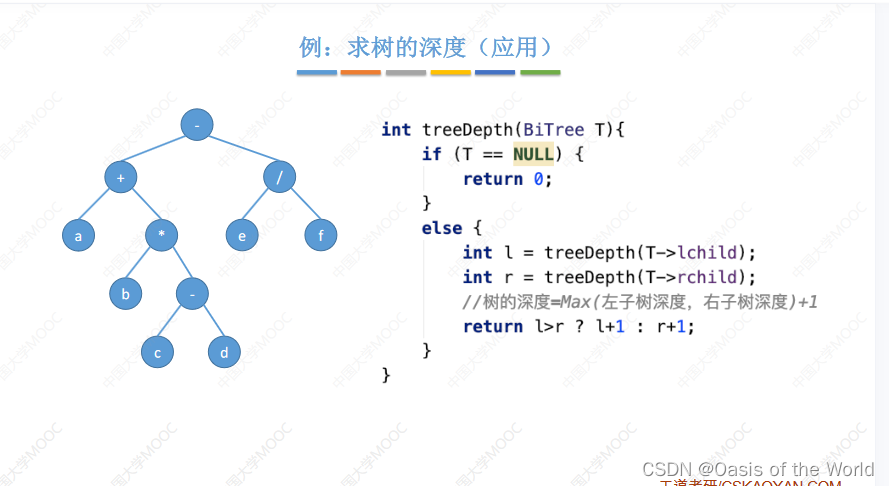
应用:求树的深度

5.2 二叉树的层序遍历
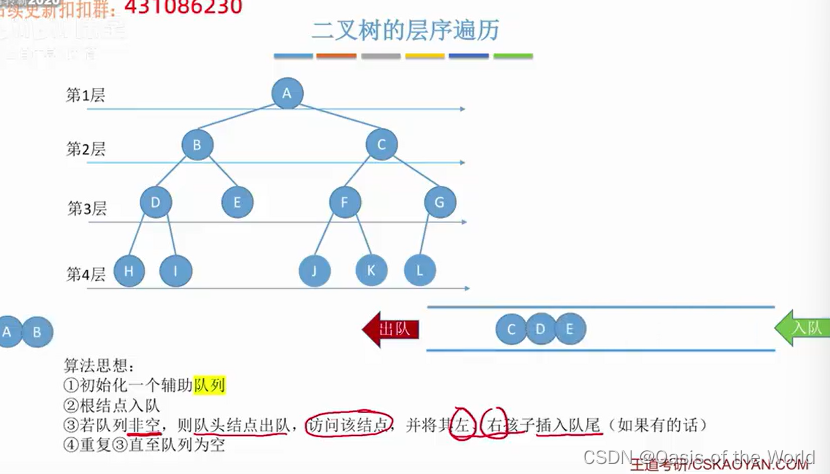
代码:

保存的是指针这样节省空间!

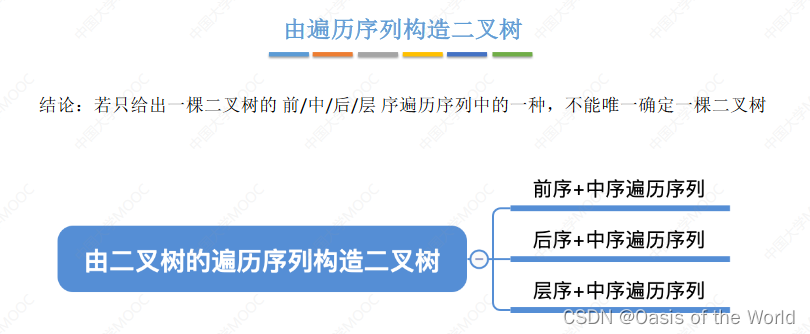
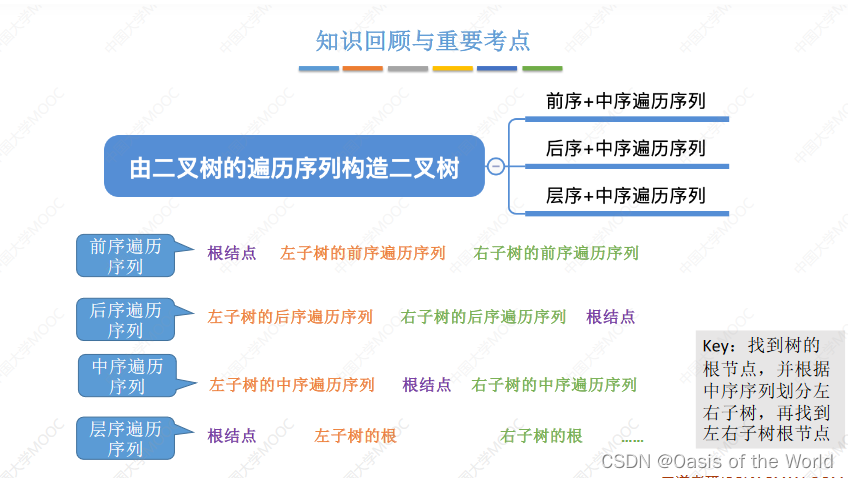
5.3 由遍历序列构造二叉树
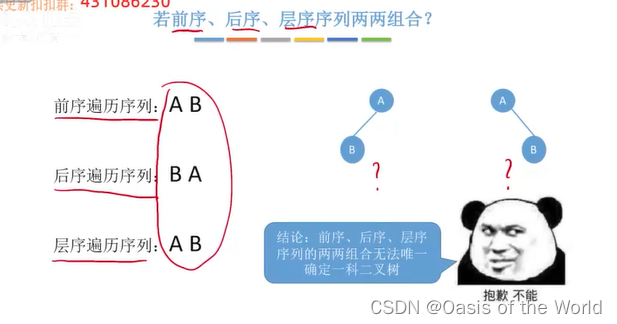
只有当两个进行组合的时候才可以确定一个二叉树!!!【必须有中序序列
!】
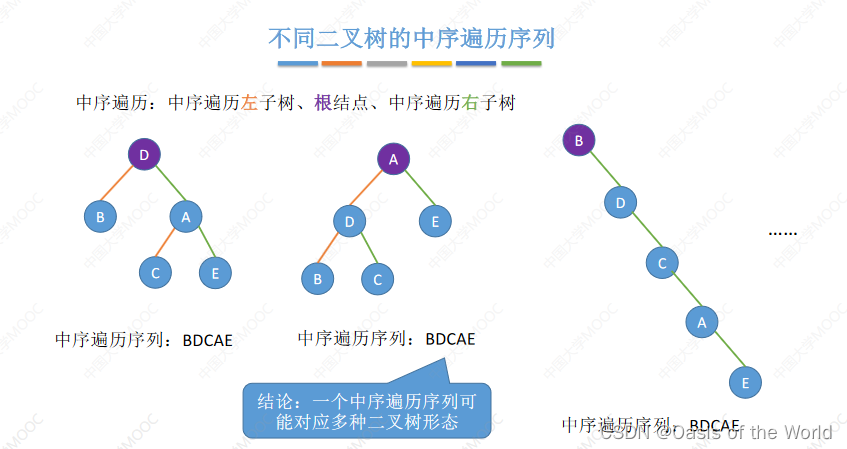
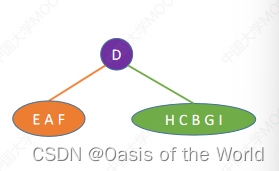
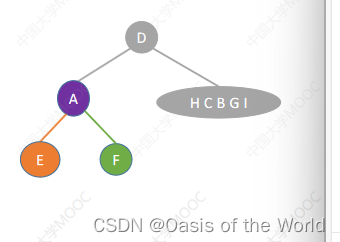
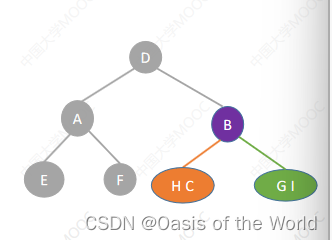
先写左子树 再写根节点 最后写右子树!
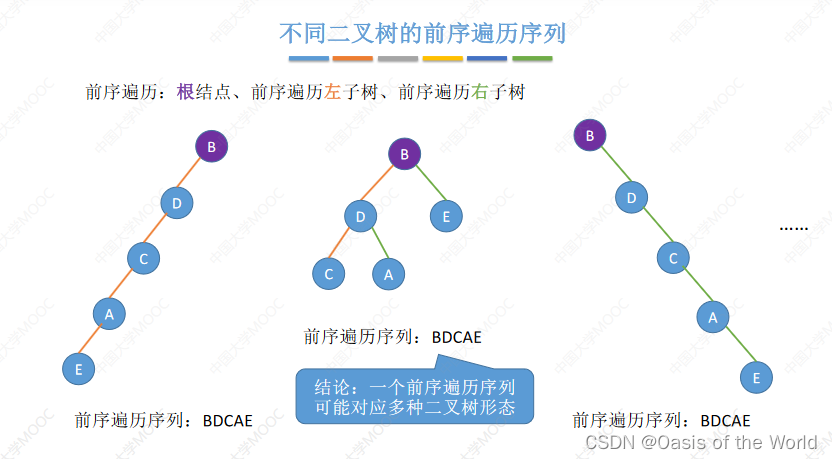
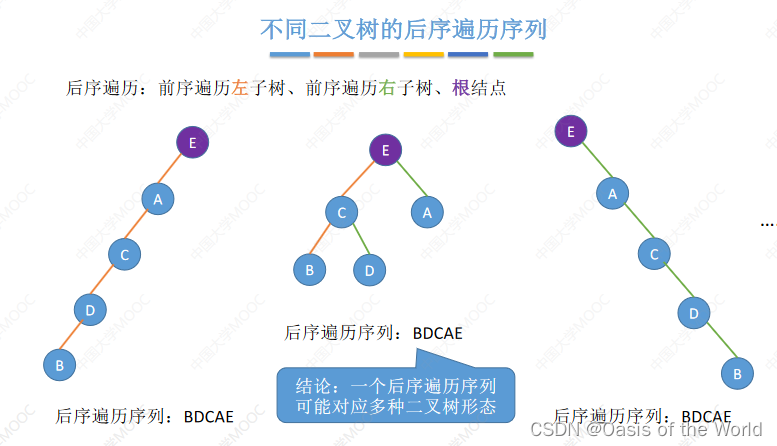

只给一个不可以,但是任意两个进行组合就可以!!!
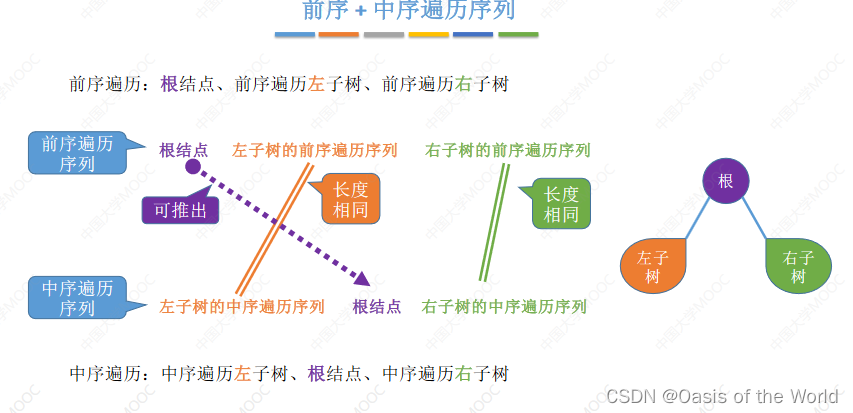
前序+中序
先圈出根结点!!!!
前序的第一个一定是根节点!!!!!
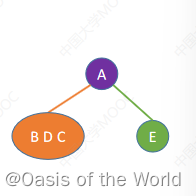
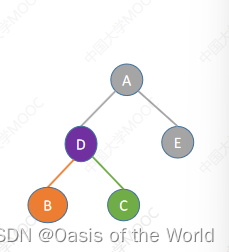
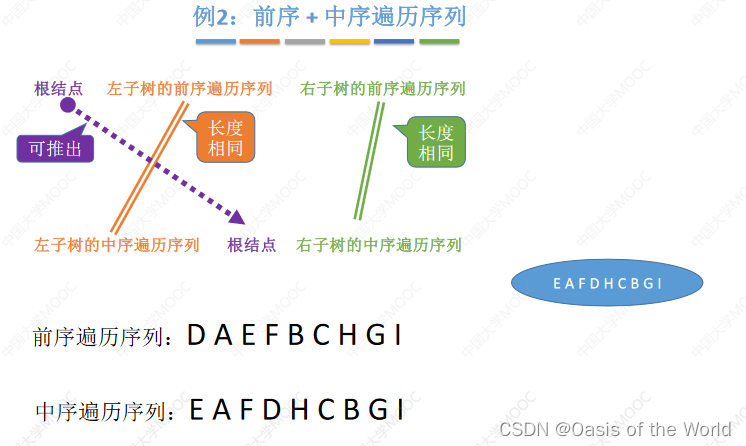
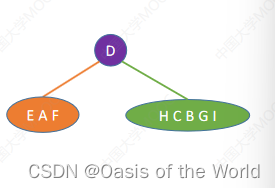
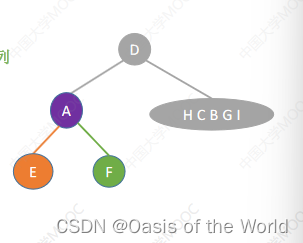
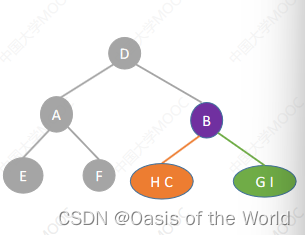
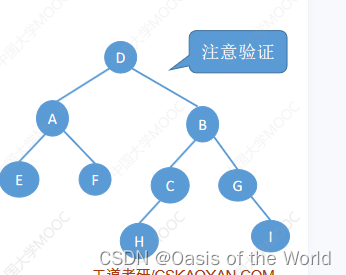
后序+中序
先找根节点:最后一个出现的就是根结点!!!!原理和之前相同!!!
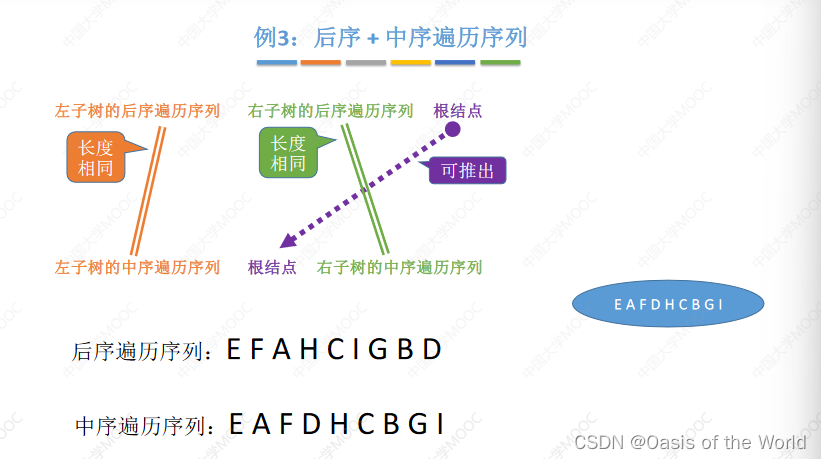
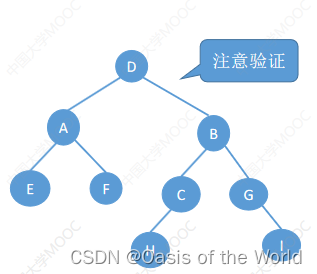
层序+中序
根节点:层次序列里先出现的就是根结点!
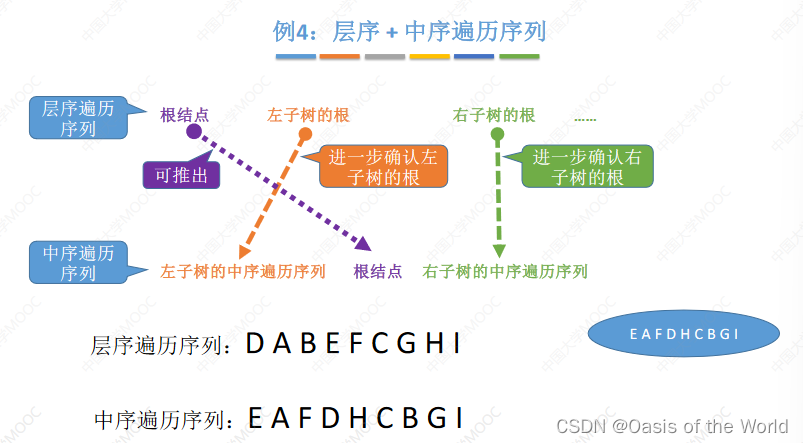
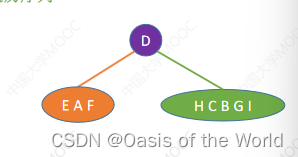
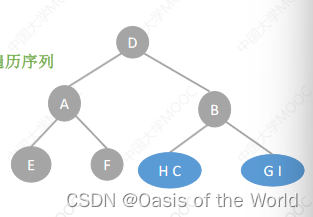
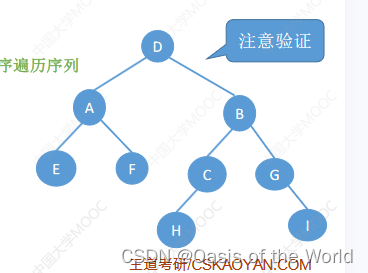
如果不要中序序列是不可以的!
6 线索二叉树【难但重要!!】
6.1 线索二叉树的作用
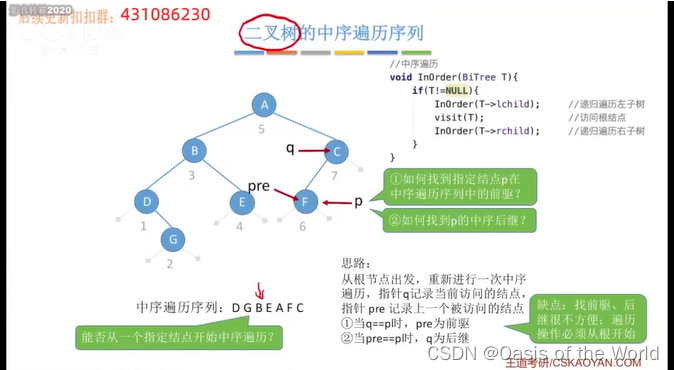
第一个问题:对于普通的二叉树 必须从根节点开始遍历才可以,不能从任意的一个节点出发进行遍历
第二个问题:找到指定结点的前驱和后继是很不方便的
所以给出了中序线索二叉树
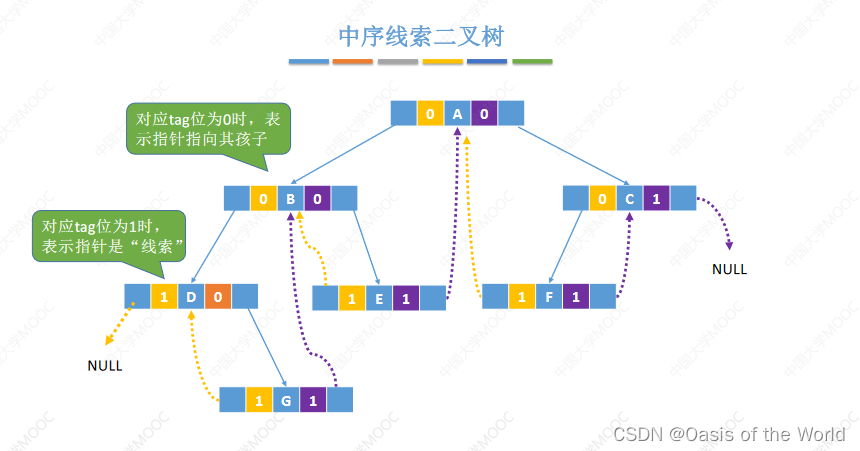
6.2 中序线索二叉树
把空链利用起来,一共有n+1个空链【n指的是结点的个数!!!】
意义:找前驱和后继就会很方便,遍历也很方便,因为遍历其实就是不断的找后继结点的过程!
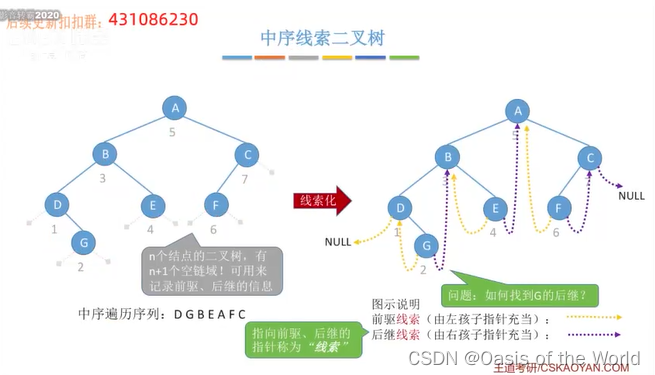
这里的前驱和后继指的是在中序遍历序列中的前驱和后继!!不是父节点子节点哦
对于优点的指向的是后孩子的结点如何找到他的后继呢?【在后边会把这个坑填上!】
6.3 线索二叉树的存储结构

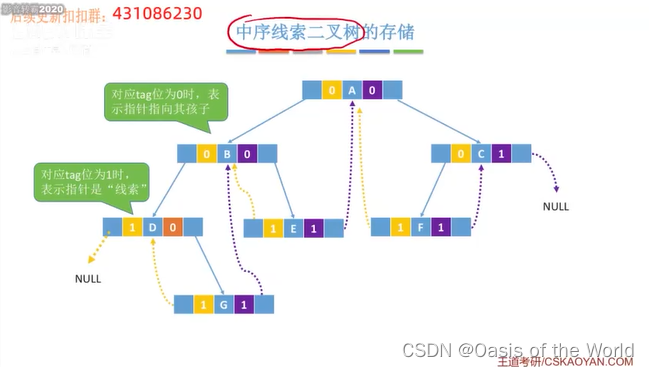

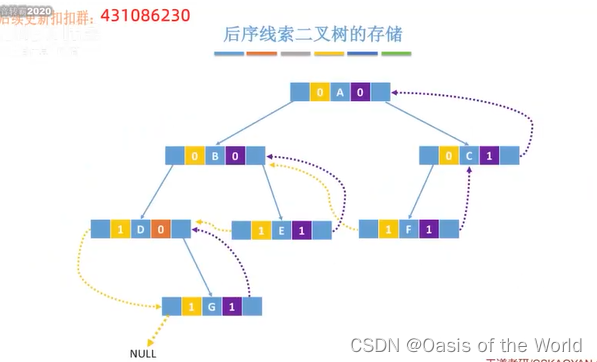


ltag==1说明是线索!
6.4 二叉树的线索化【代码实现!!】
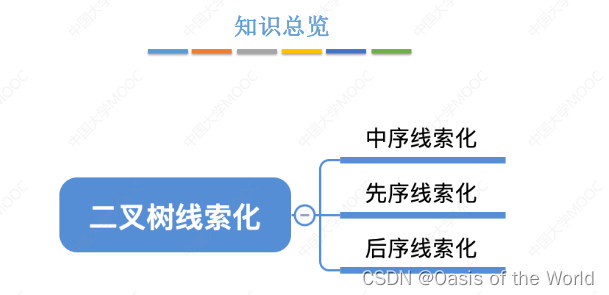
6.4.1 土方法找中序前驱
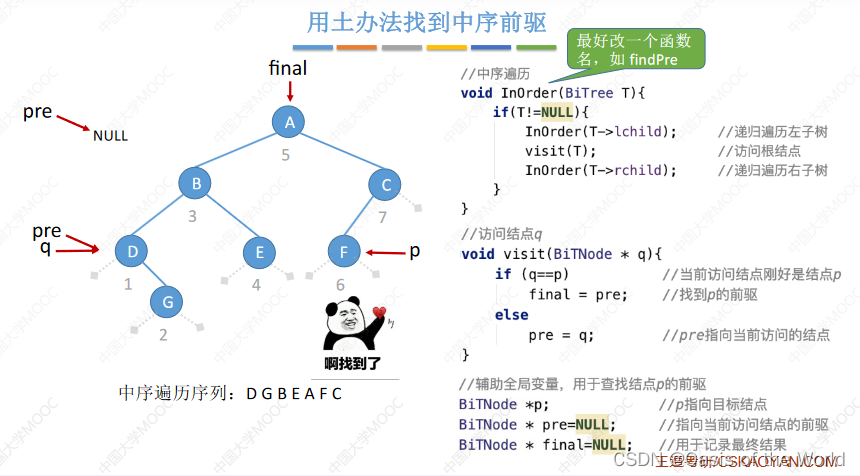
6.4.2 中序线索化
线索化的过程其实和“土方法”是一样的,只不过每走一步就要判断一下是否有空链有就连上线索!
判断时:
【pre时p的前驱】看pre的右节点是否为空,空的话就连上p;看p的左节点是否为空,空的话连上pre

注意这个过程中没有最后一个结点的右指针指向null,需要做特殊处理!
下面是完整的代码!:


pre定义成局部遍历了,用引用之后会改变pre的值,和在外面定义一个是一样的!
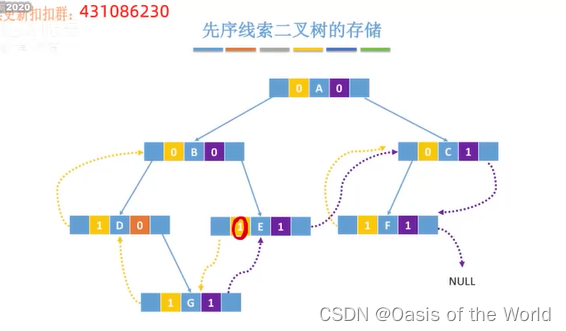
6.4.3 先序线索化
会出现爱的魔力转圈圈的问题
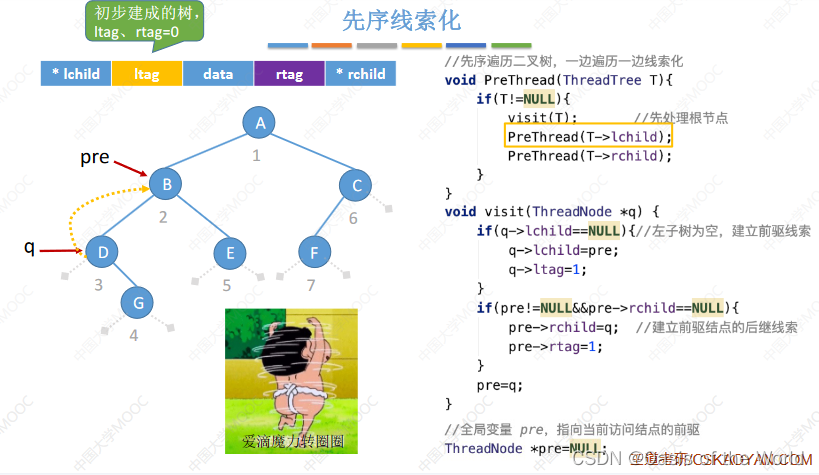
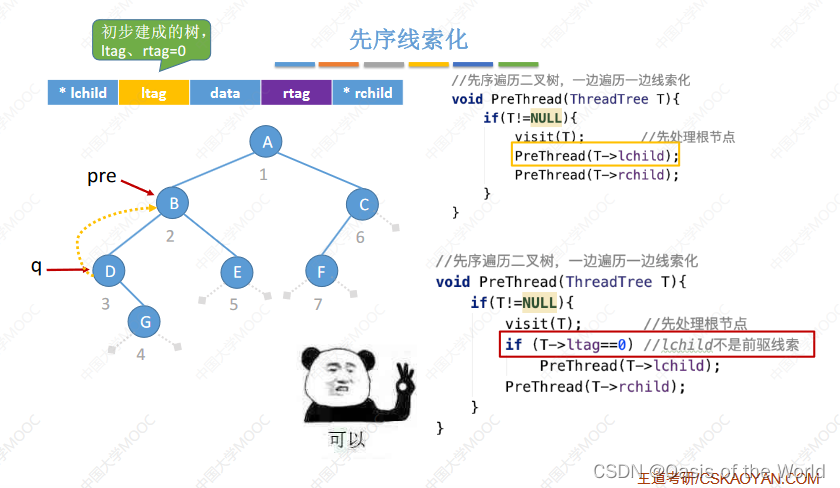
完整代码:【也要对最后一个结点做特殊处理!】


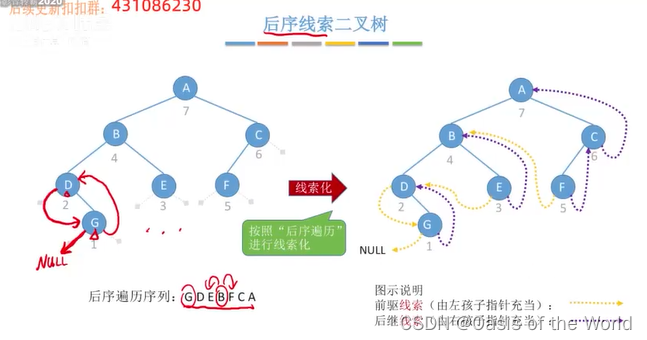
6.4.4 后序线索化
不会出现爱的魔力转圈圈的问题!


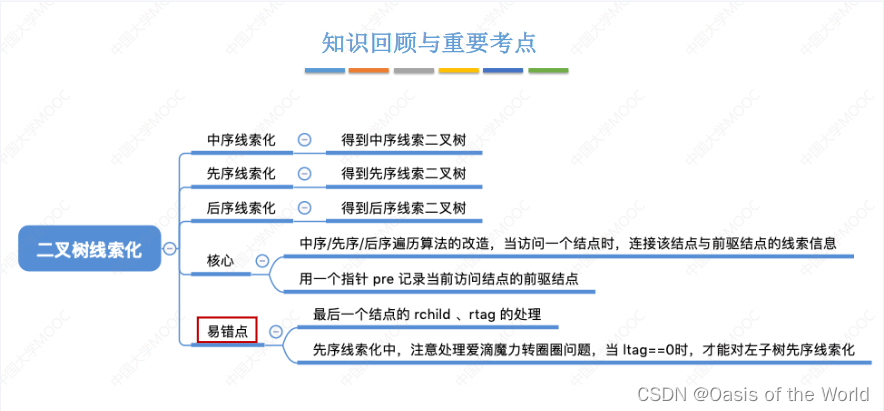
6.5 在线索二叉树里找前驱和后继
更方便二点找到前驱和后继!!!
后序后继,和前序前趋 都需要能找到父节点才可以!!!!【用三叉链表或者土办法才可以】
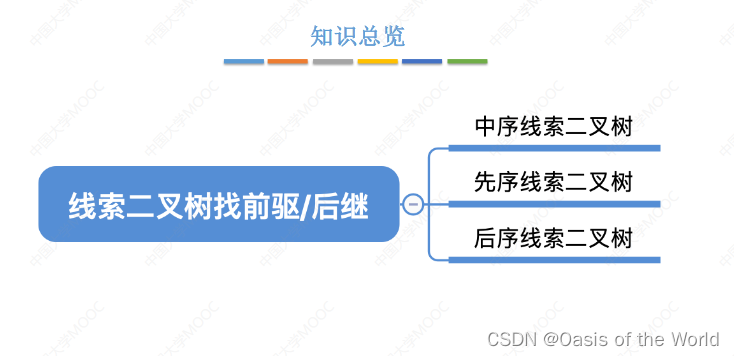
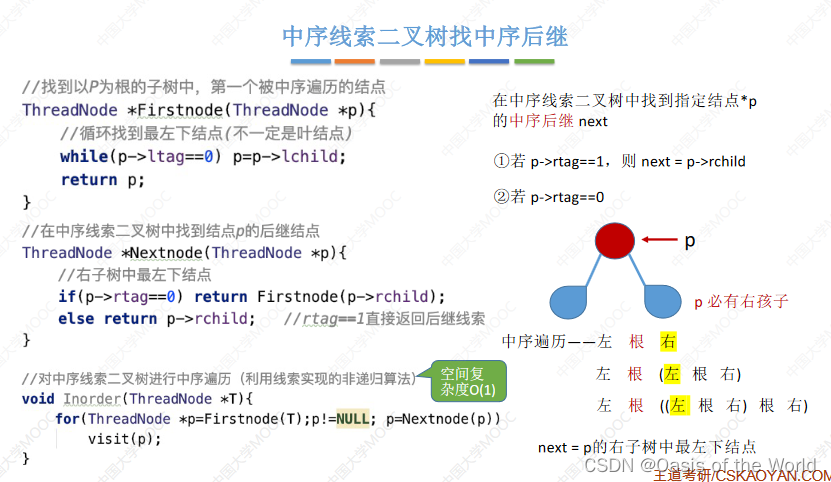
中序后继
当tag=0的时候进行展开,注意展开到挨着“根”就停止了!

当有右孩子的时候,这个结点的后继结点就是p右子树的最左下的结点!!!
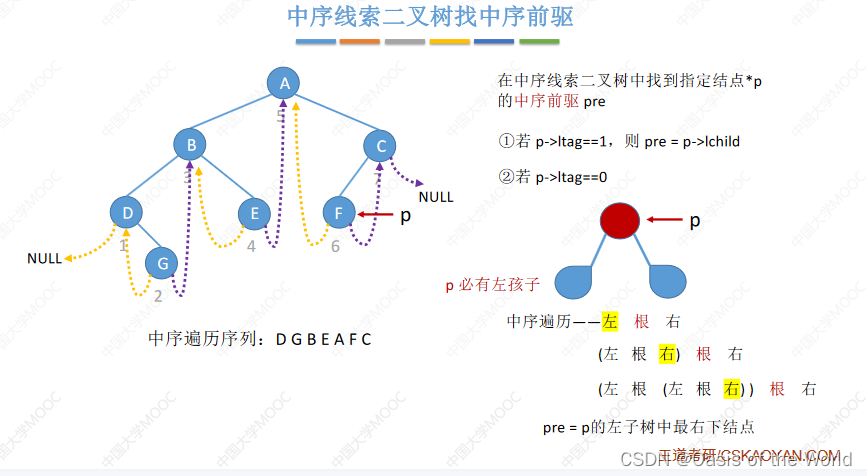
中序前驱
左子树的最右下的节点!!时刻确定tag

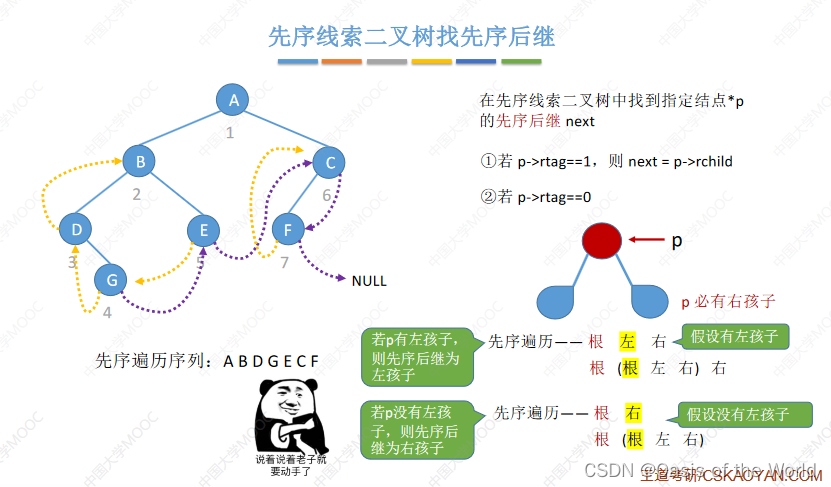
先序后继
如果有左孩子那么就是左孩子,如果没有左孩子那么只能是右孩子!
先序前驱
当ltag = 0时,就找不到前驱了,只能通过土办法进行寻找,因为没有往回指的指针了!【当可以找到父节点的话此局可解!】

如果能找到父节点的话:
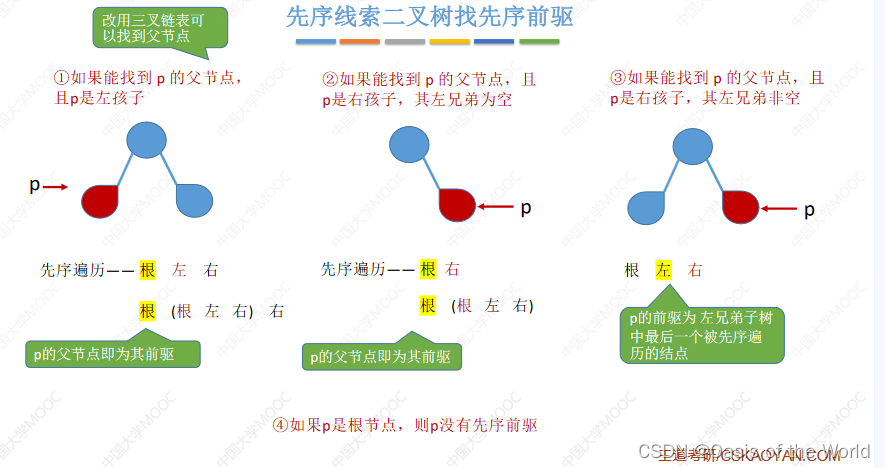
对于3优先往右走,如果可以走通就一直走,走不了就向左拐下去就一直到最后一层就是它的前驱!!!
后序前驱
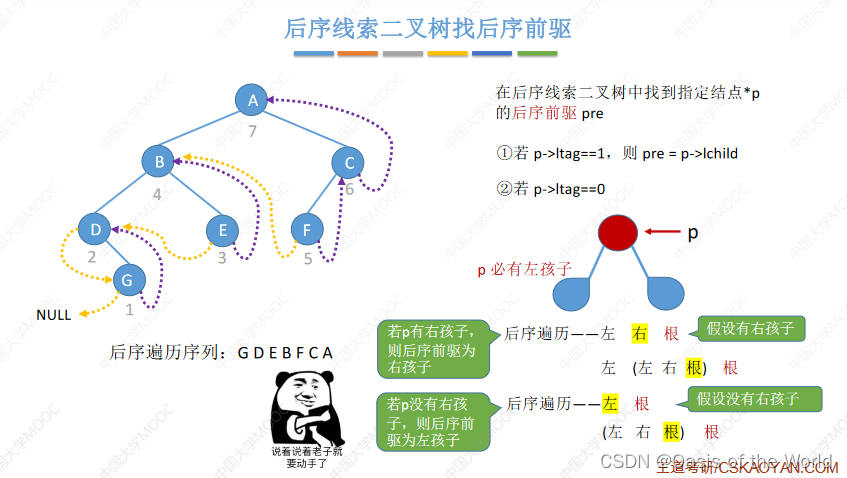
后序后继
只能用土办法!!!如果可以找到父节点的话此局也可解
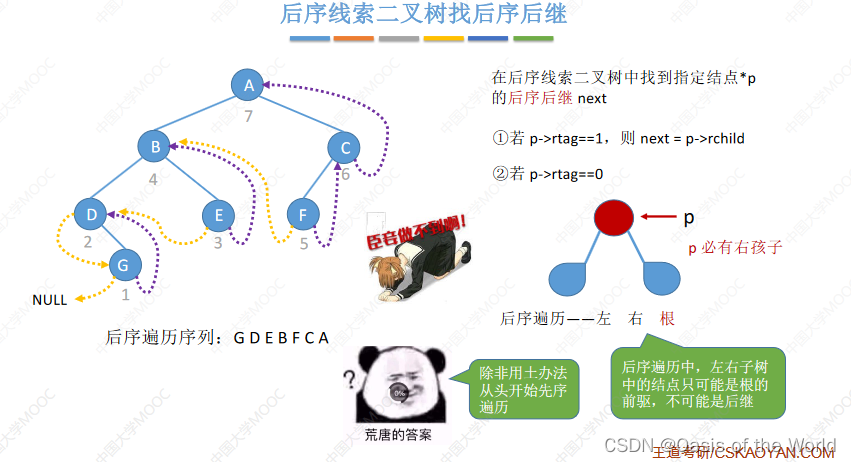
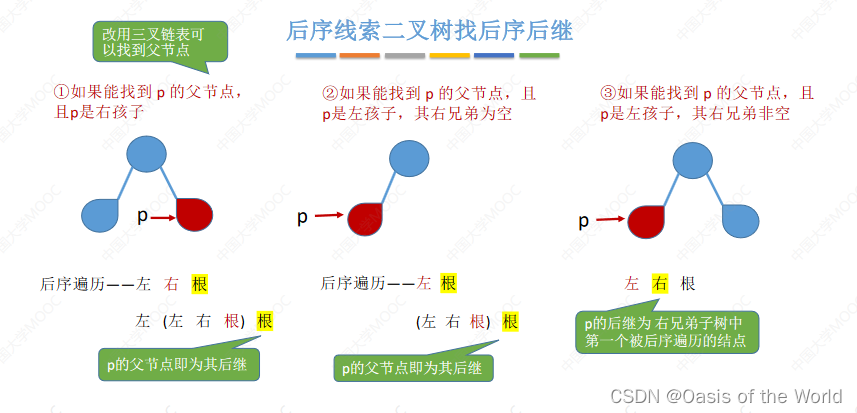


7 树和森林
7.1 树的存储结构

二叉树的顺序存储:

是否可以推广到普通的树呢?

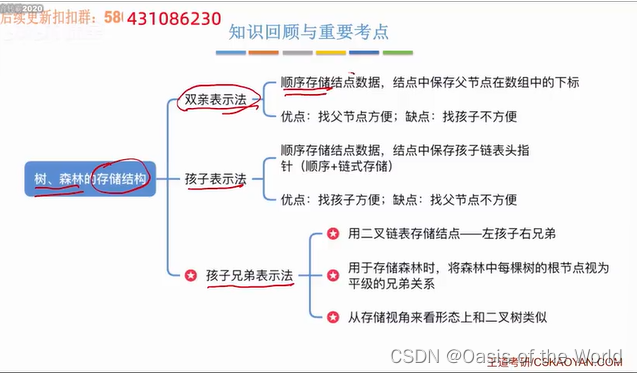
7.1.1 树的存储1:双亲表示法【顺序】
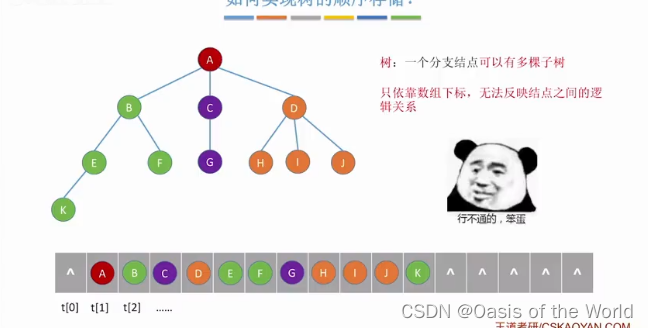

拓展:
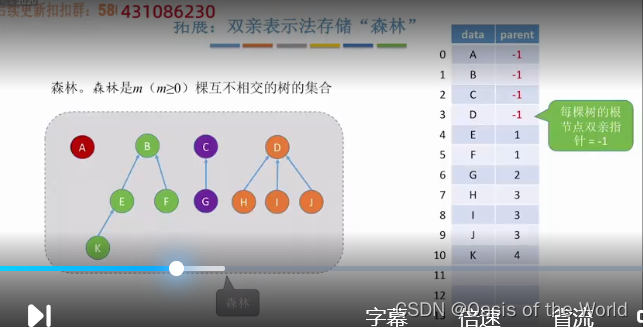
优缺点:
找父节点【很方便!!!】,找孩子结点【只能遍历一下数组!!!】

7.1.2 树的存储2:孩子表示法【顺序+链式】
firstchild:指向第一个孩子编号!
用一个链表记录一个节点的孩子编号!

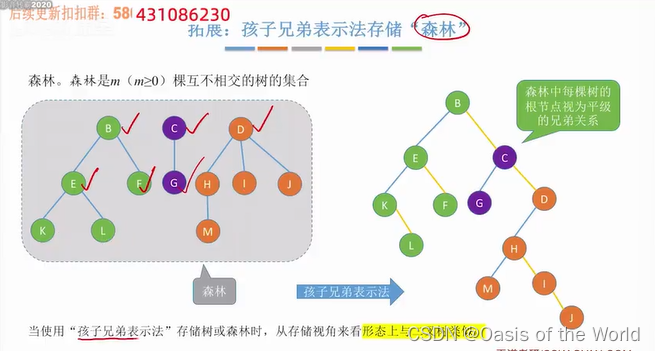
拓展:孩子表示法存储森林

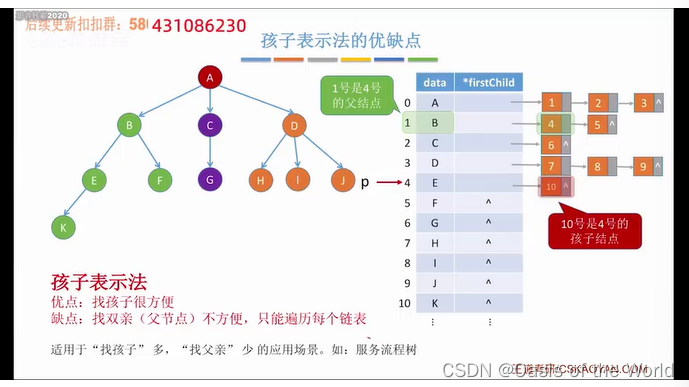
服务流程树:
中文服务请按1,英文服务请按2.....按完之后又会接着要求按什么?直到找到具体的服务
7.1.3 树的存储3:孩子兄弟表示法【纯链式存储】
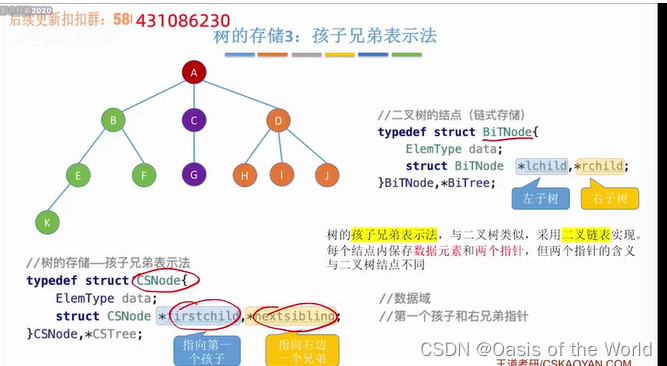
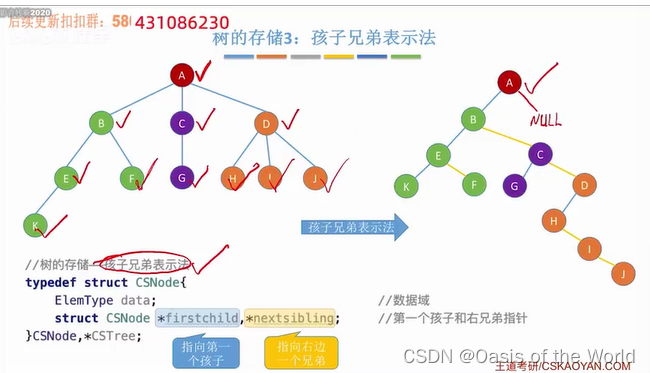
从用孩子兄弟表示法的结果来看很像二叉树!
拓展:孩子兄弟表示法存储森林
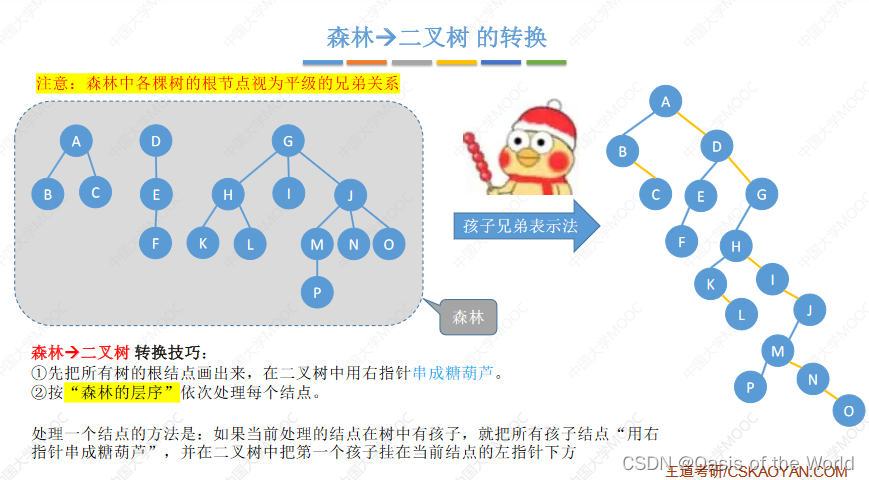
树根视为平级的兄弟关系
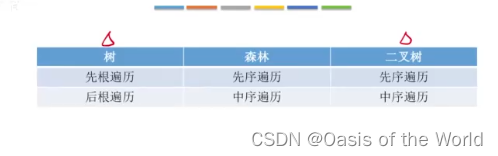
7.2 树、森林与二叉树的转换【重要】

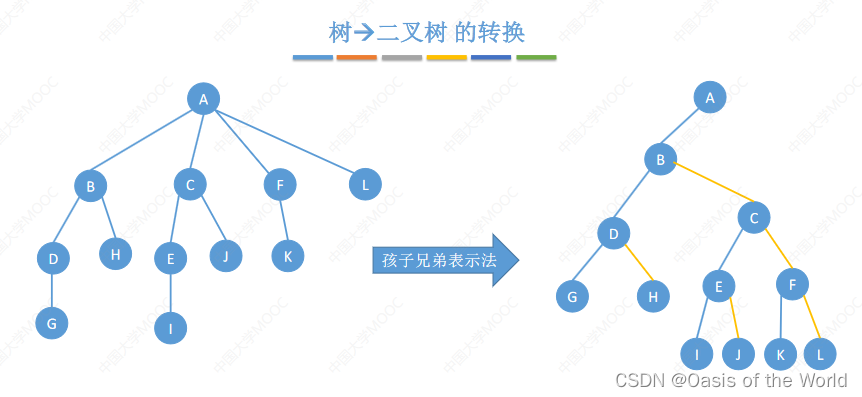
7.2.1 树转二叉树
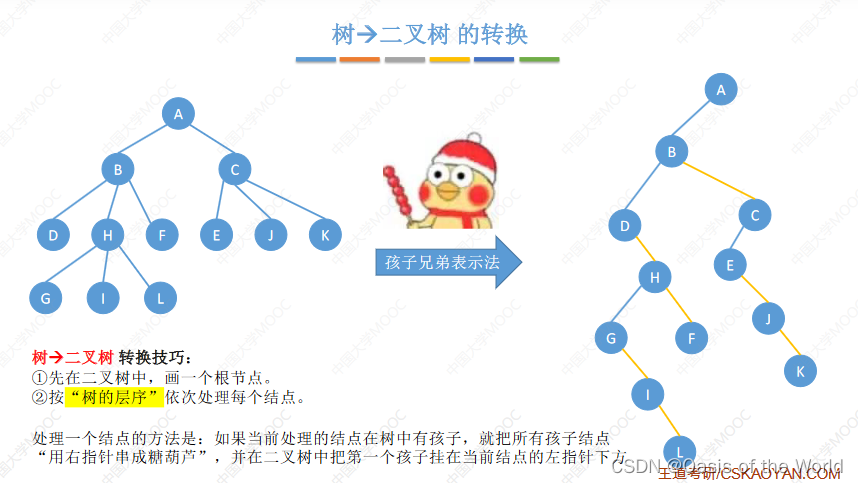
一层一层的处理,串冰糖葫芦!
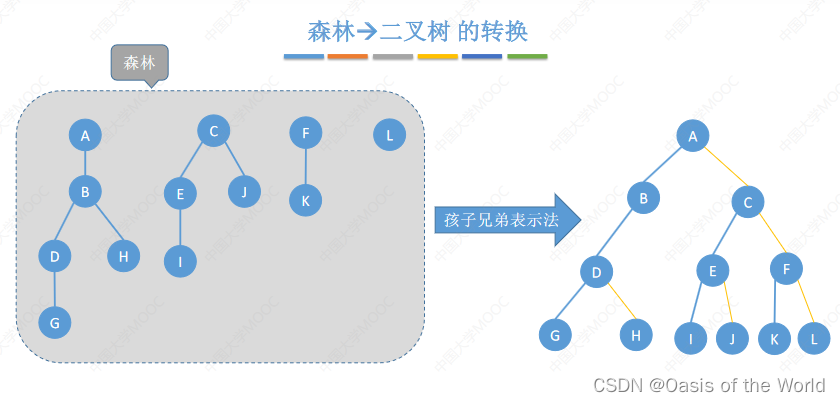
7.2.2 森林转二叉树
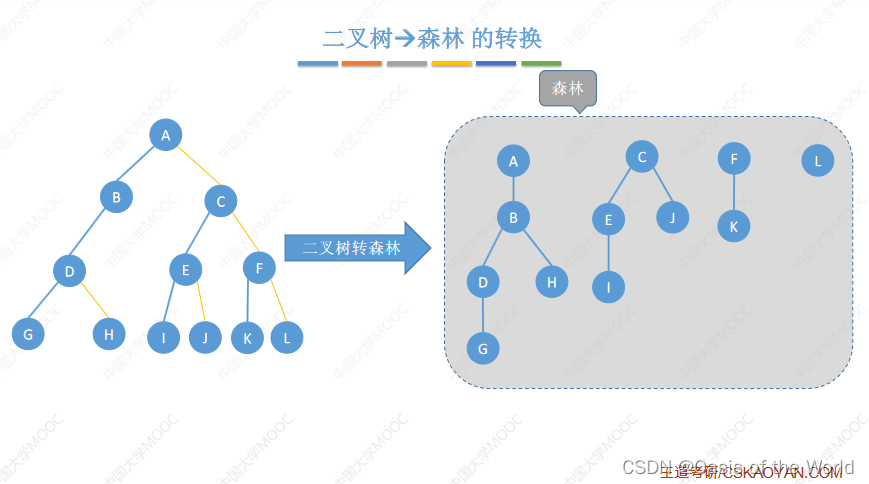
7.2.3 二叉树转树
把冰糖葫芦先圈出来,然后 按照二叉树的层数放冰糖葫芦!



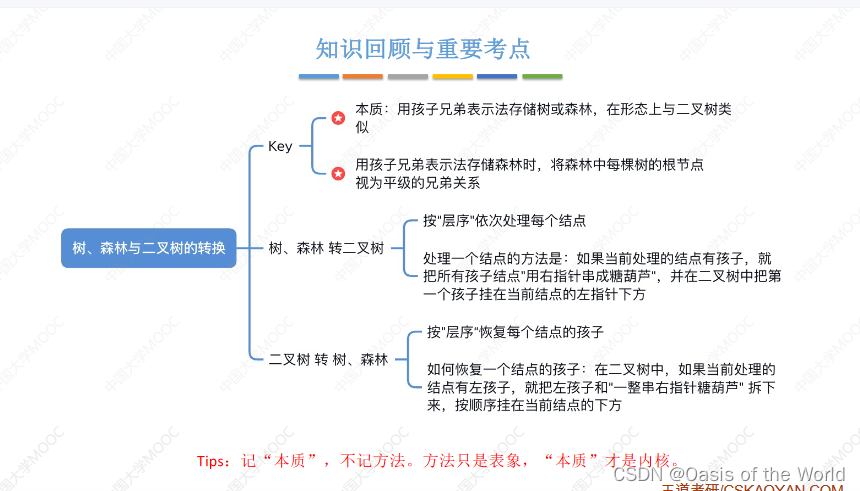
7.3 树和森林的遍历
8.2 森林转二叉树

树是一个递归定义的东西!

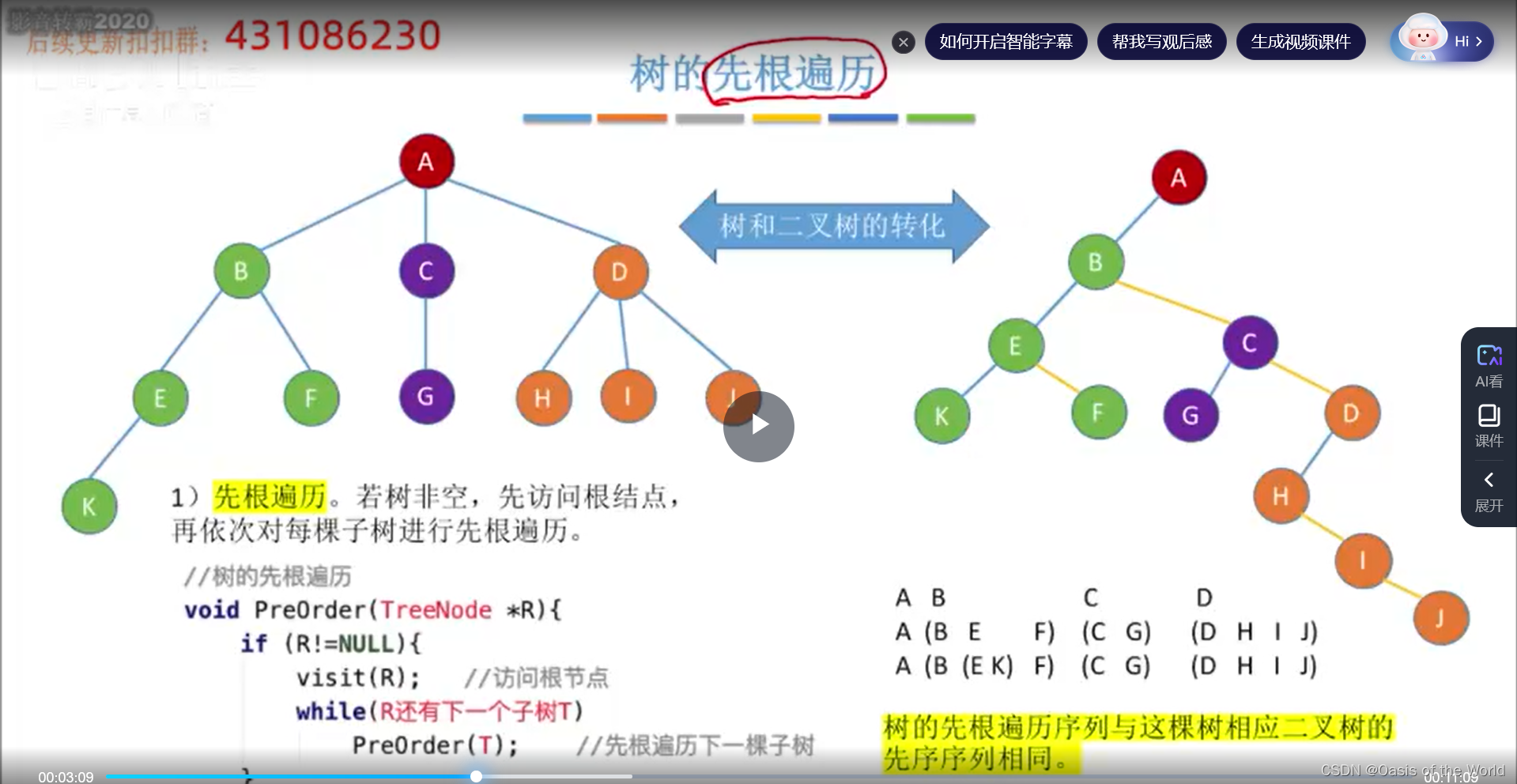
7.3.1 树的先根遍历【深度优先遍历】
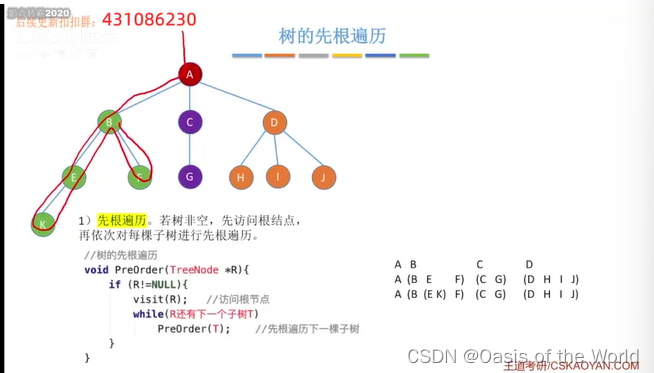
这个路径优先往左走,然后每到一个就visit
7.3.2 树的后根遍历【深度优先遍历】

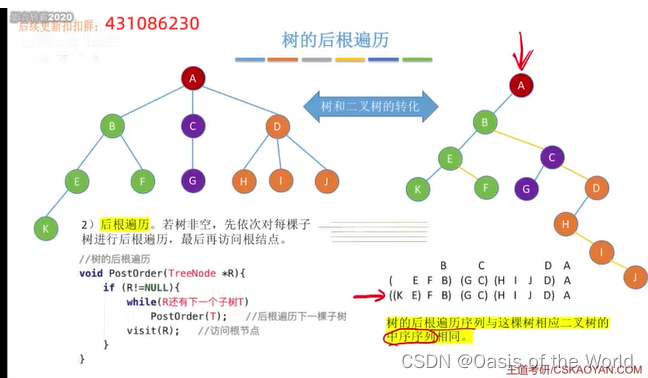
路径也是优先往左往下走,当第二次路过该节点的时候visit
7.3.3 树的层次遍历【广度优先遍历】
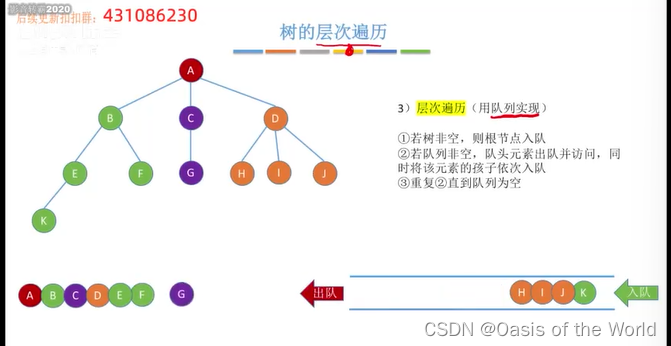
可以发现路径是尽可能一层一层的遍历的!所示可以看作是广度优先遍历
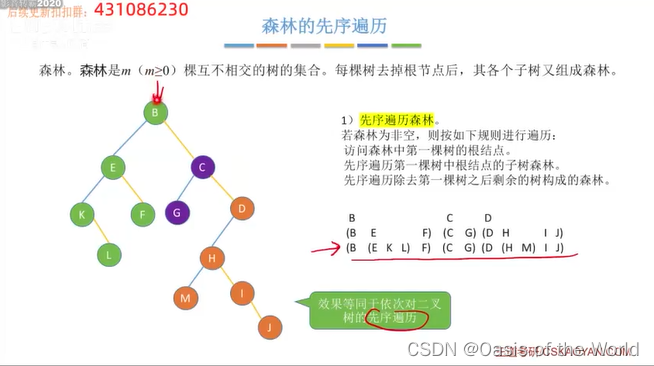
7.3.4 森林的先序遍历
森林这种数据结构适合树相互递归定义的!
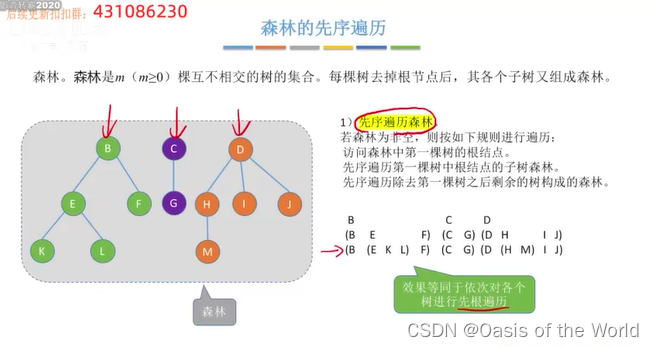
注意递归的时候:第二部如果访问到的还是森林的话会回到第一步!
7.3.5 森林的中序遍历[看不懂如何递归的!!!!!!]
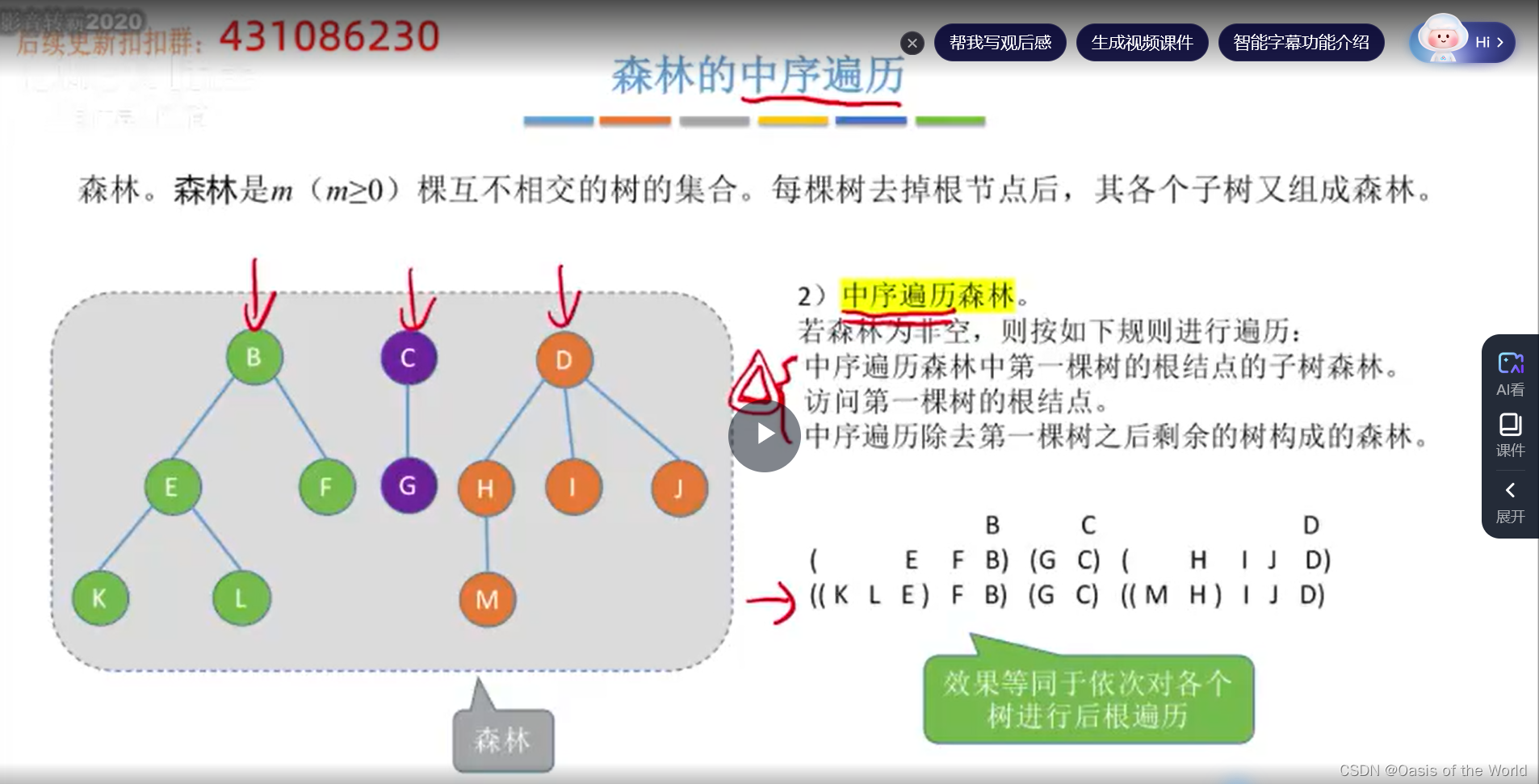
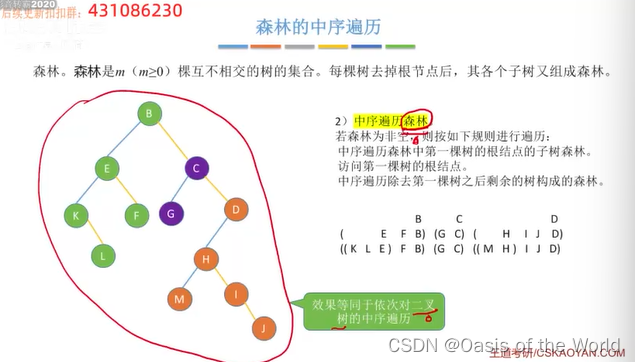
8 树与二叉树的应用
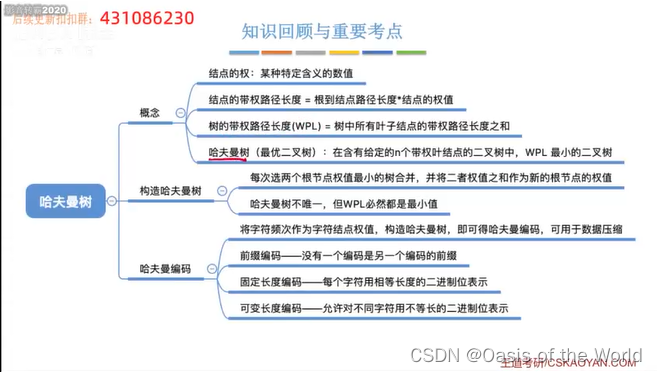
8.1 哈夫曼树【数据的压缩】
重要在哈夫曼树的构造!和哈夫曼的应用--哈夫曼编码!


只计算所有叶子节点!

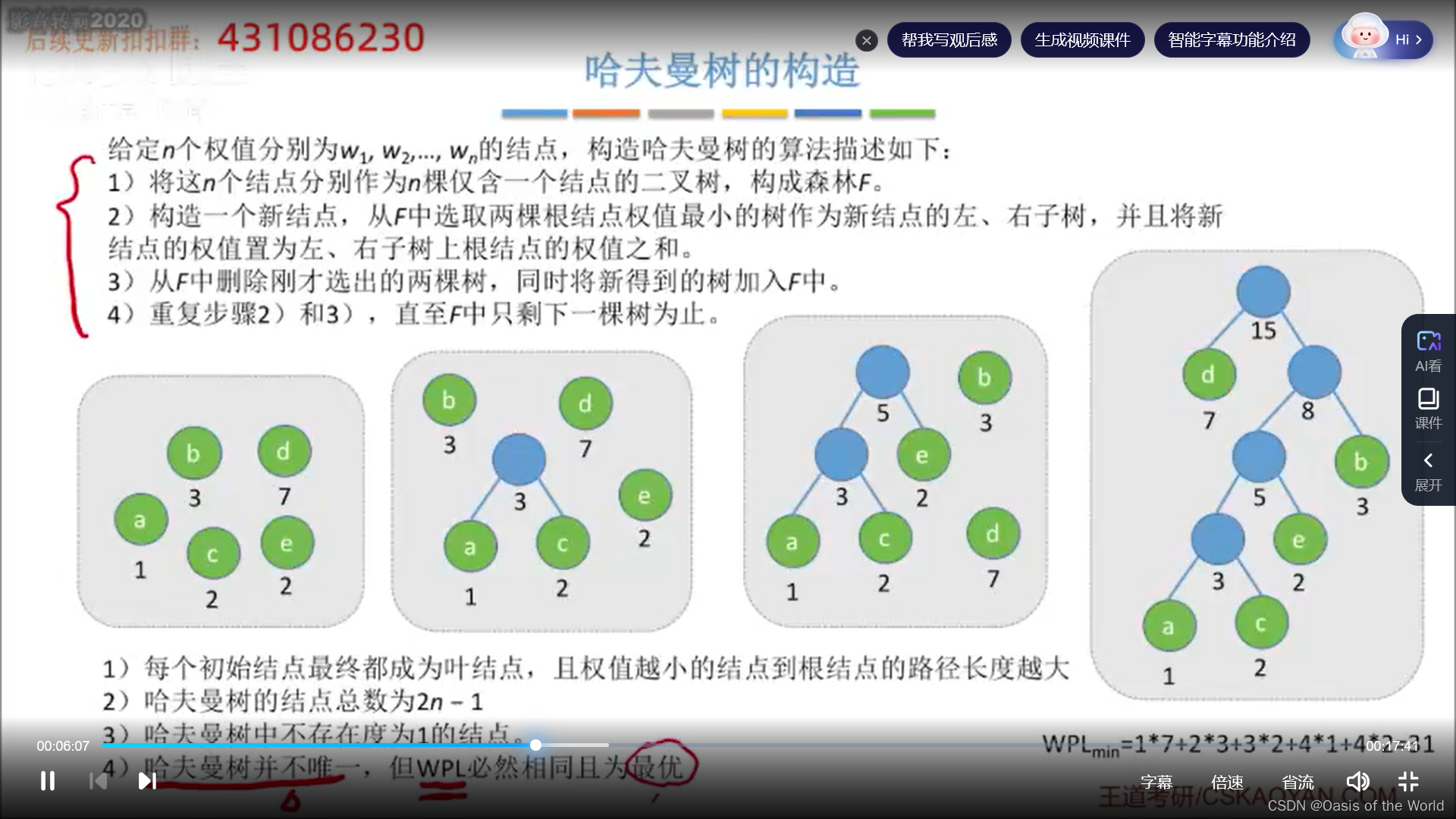
哈夫曼书的定义:
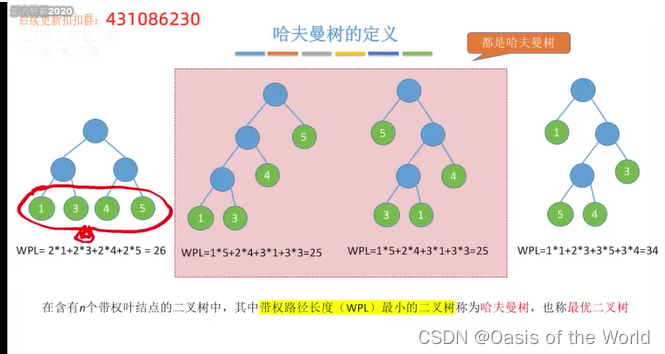
如何构造呢?
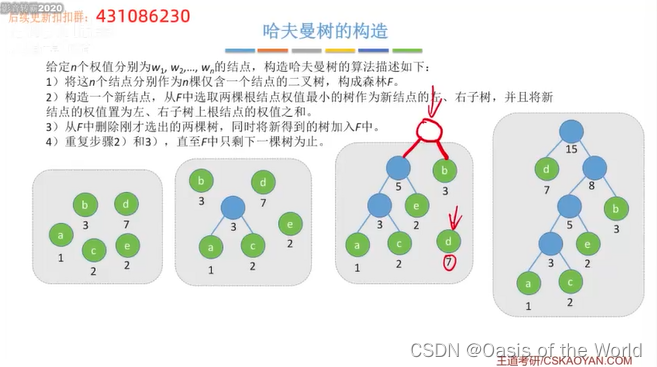
更小的先结合!
一共需要合并n-1次,每次合并都会出现一个新的结点则哈夫曼树一共有2n-1个结点!
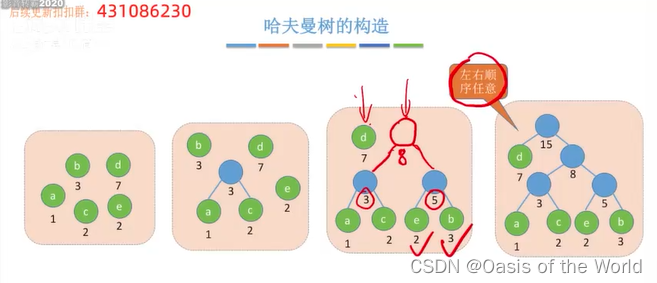
同样的叶子节点可以构造出不同的哈夫曼树
哈夫曼树的经典应用:哈夫曼编码
![]()
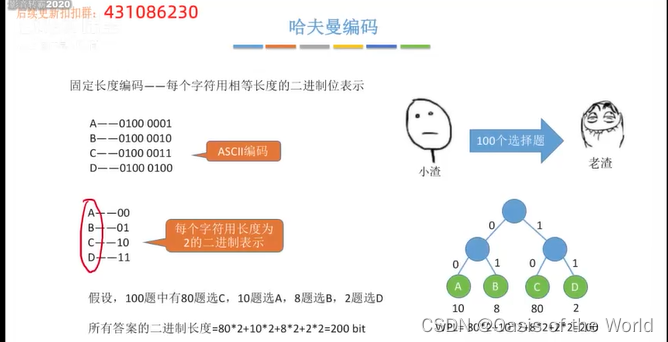
有没有比这个方案更有效的方案呢?
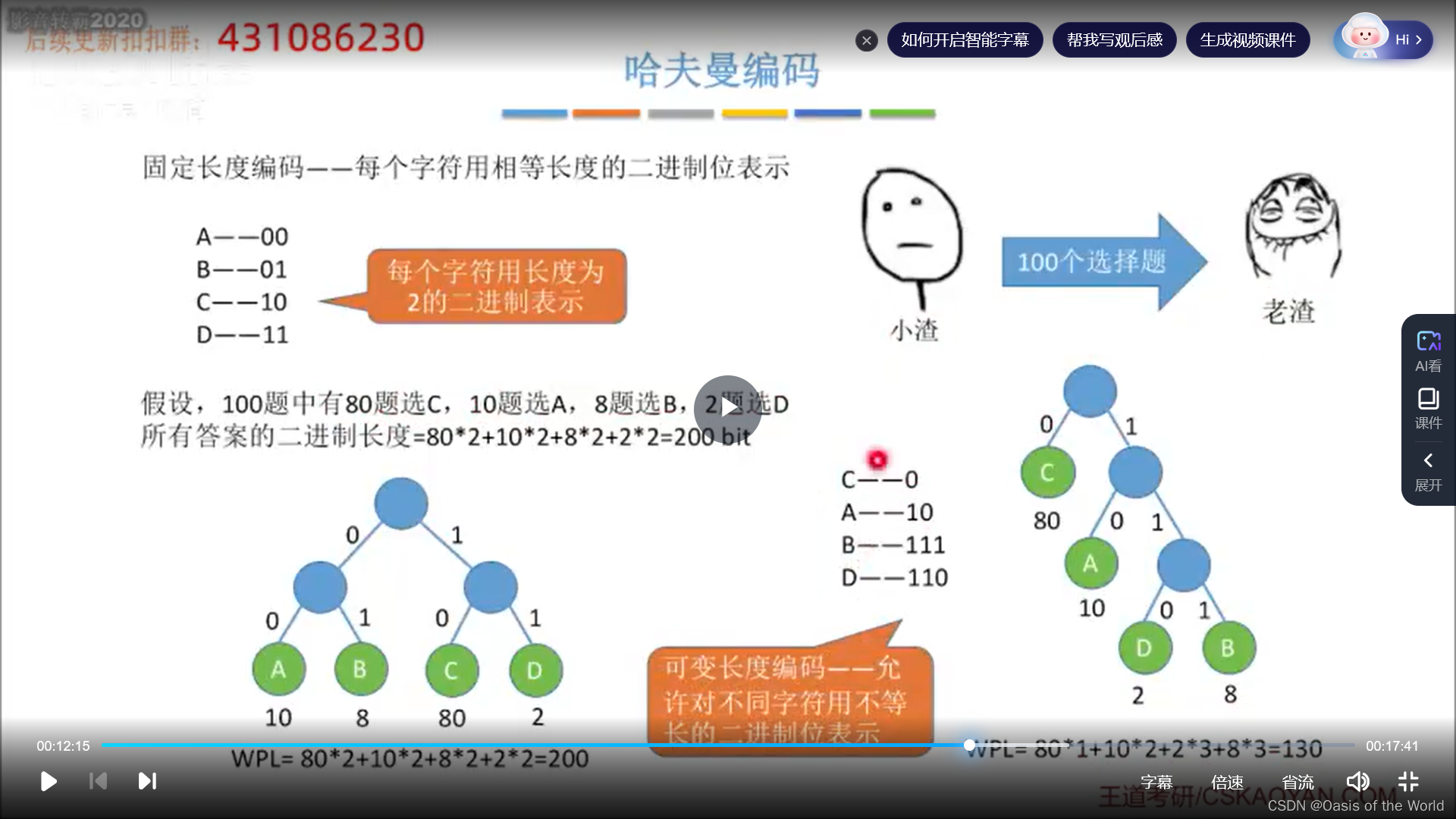
能不能更简单呢?
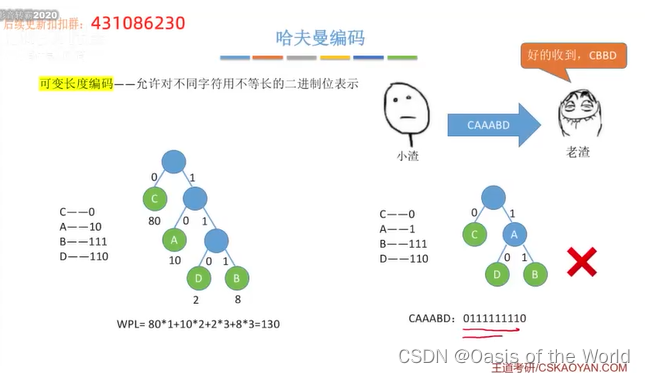
右边的编码可能会导致解码错误!
因此对可变长度编码时,所有的字符集对应的字符必须作为叶子结点不能作为中间的结点!
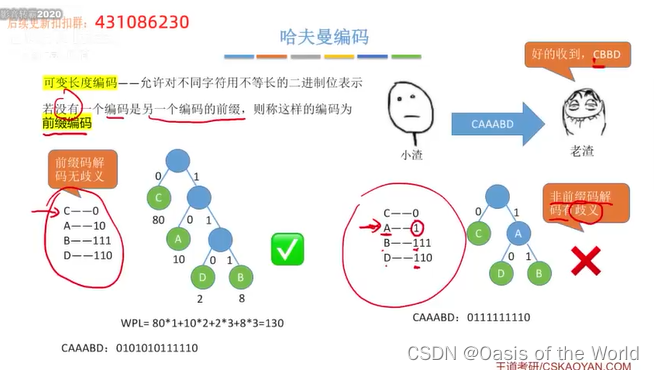
前缀编码:没有一个编码是另一个编码的前缀!
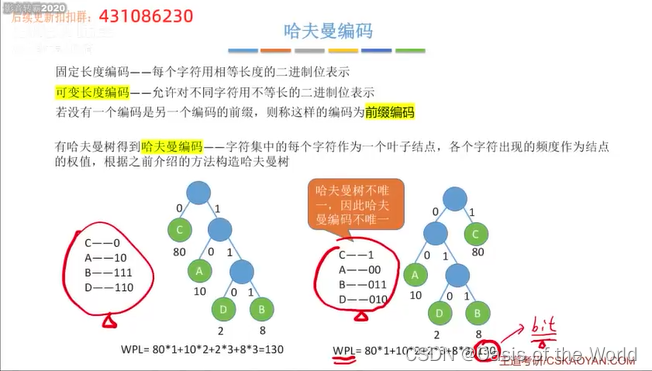
因此哈夫曼树可以用于数据的压缩!
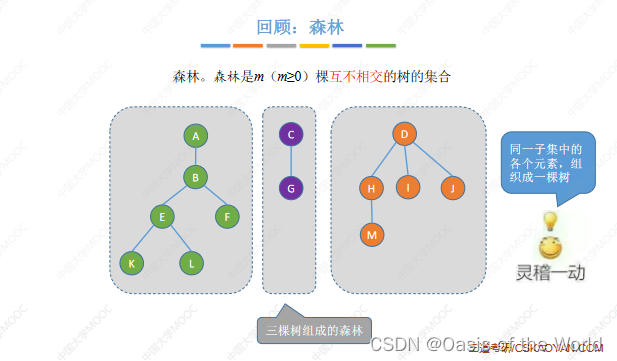
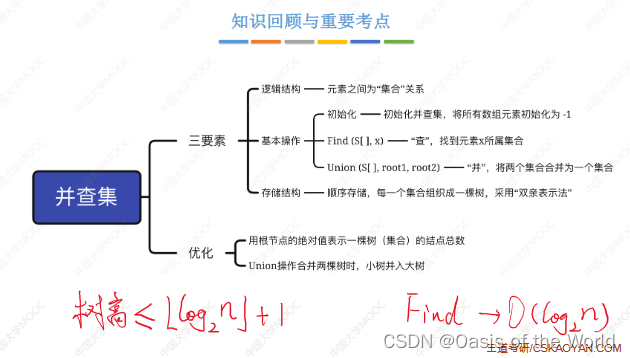
8.2 并查集

各个集合之间是互不相交的,两个元素只有两种关系:一个是从属于同一个集合,一个是在不同的集合里
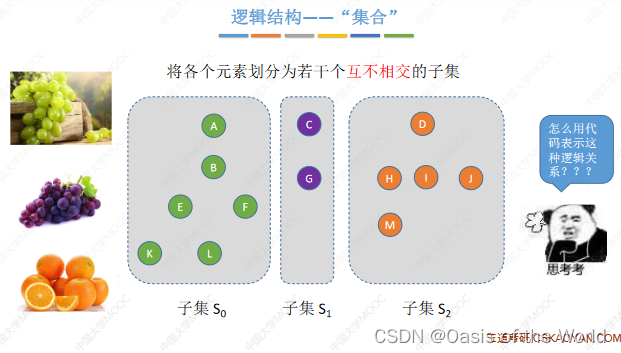
怎末用代码实现这样的数据结构呢?
使用森林:同一个集合中的元素组成树!
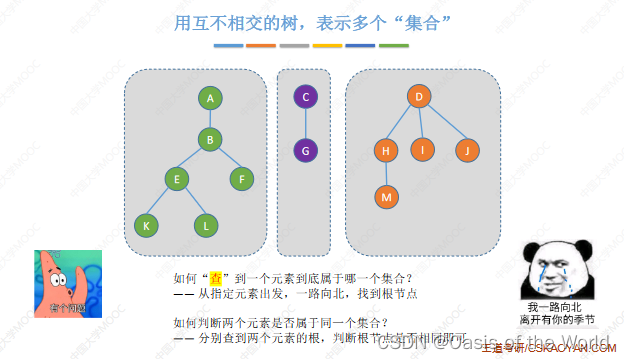
查:一路向上找到根节点!找根即可
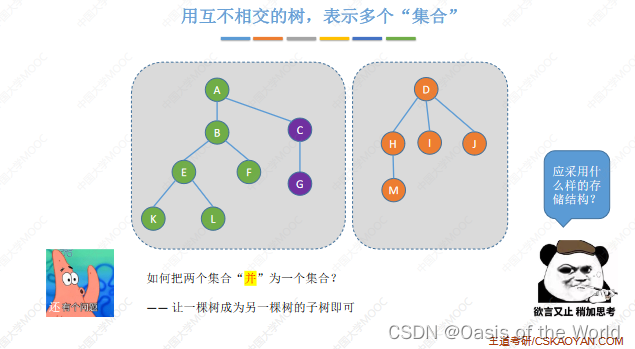
并让一个树称为另一棵树的子树!
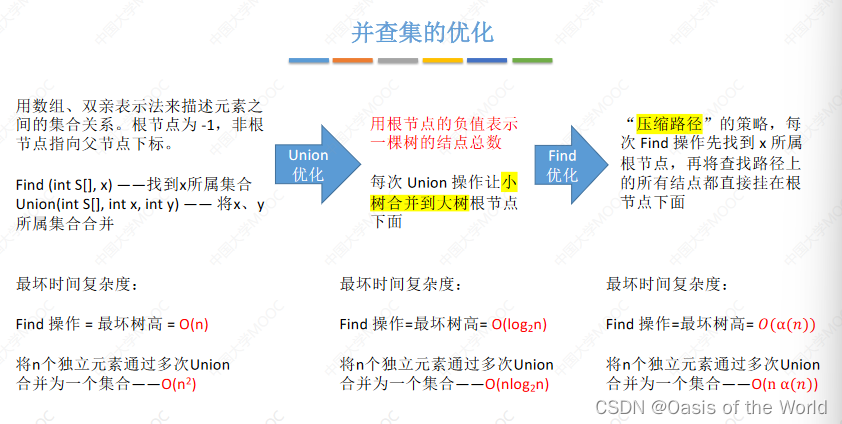
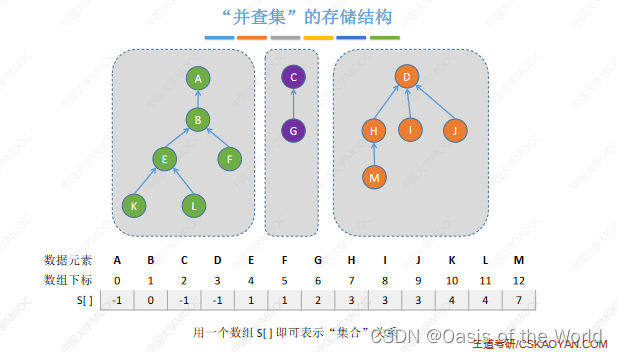
树的存储:双亲表示法、孩子表示法、孩子兄弟表示法。【双亲表示法会更适合实现并查集】

双亲表示法可以很快的找到父节点方便进行并和查的操作
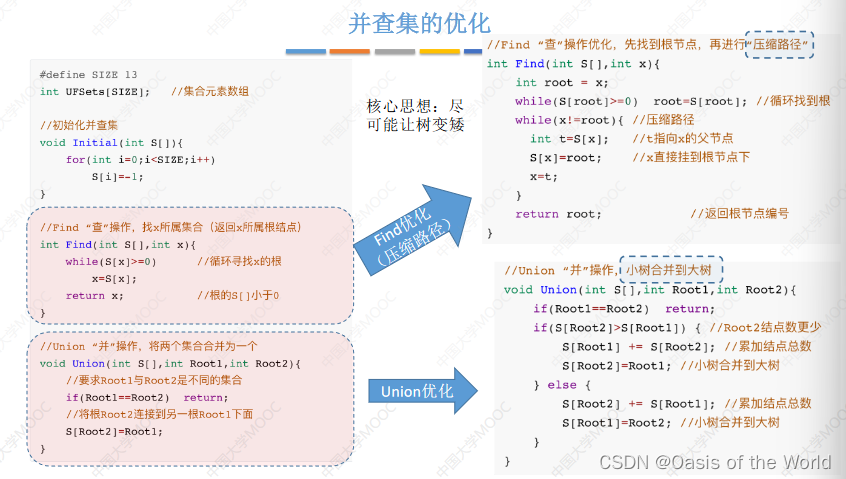
8.2.1 存储结构
8.2.2 基本操作
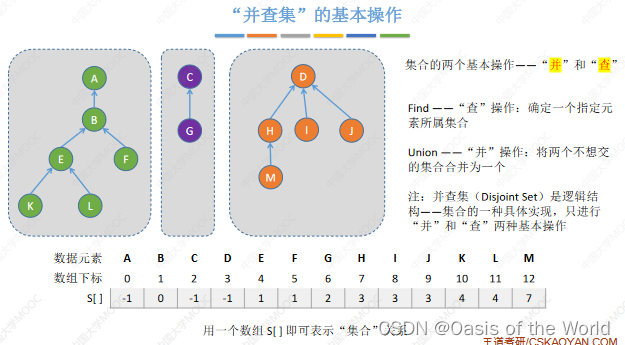
是集合的具体实现
8.2.3 代码实现
【1】初始化
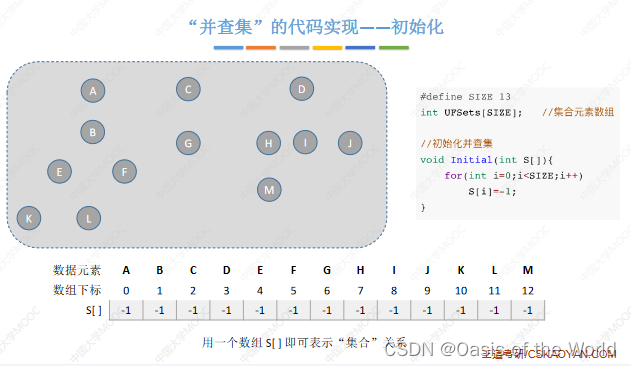
【2】并查
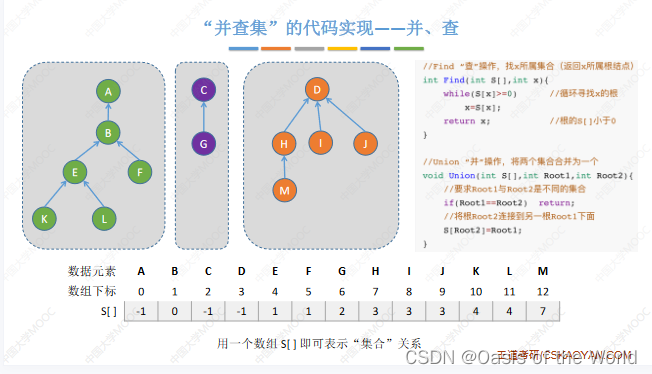
并的操作:是传入两个根节点的编号
【3】时间复杂度

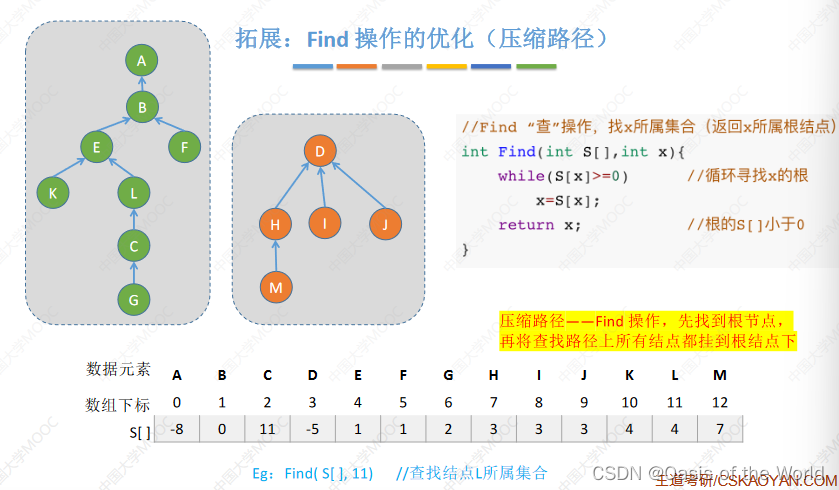
find最坏时间复杂度:o(n),和树的高度有关,则如果对算法进行优化,意思就是让树长的不要那么瘦高!
【4】union优化(让小树合并到大树上就不会增加树的高度了)


大树小树:用根节点的绝对值表示树的结点总数!
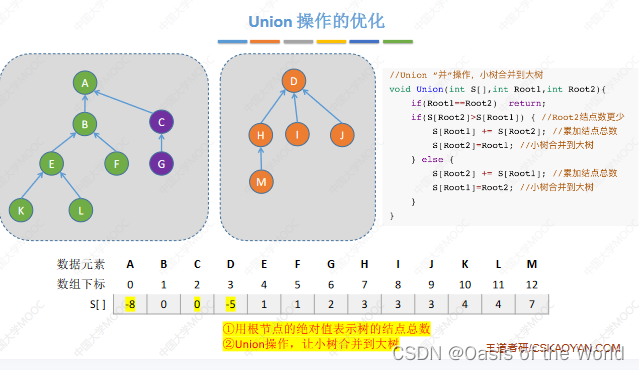
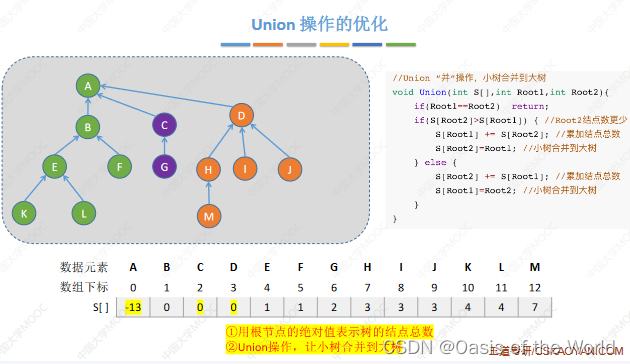
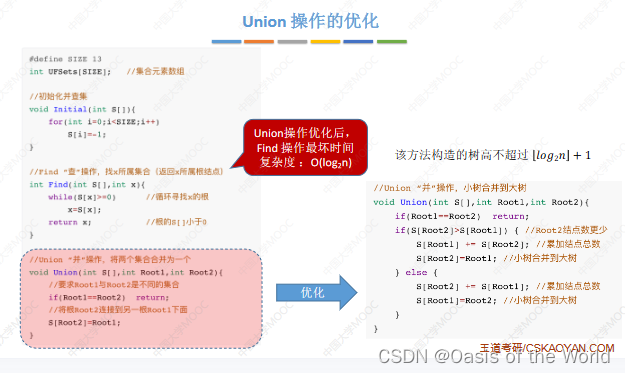
树的高度不会超过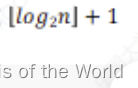 、
、


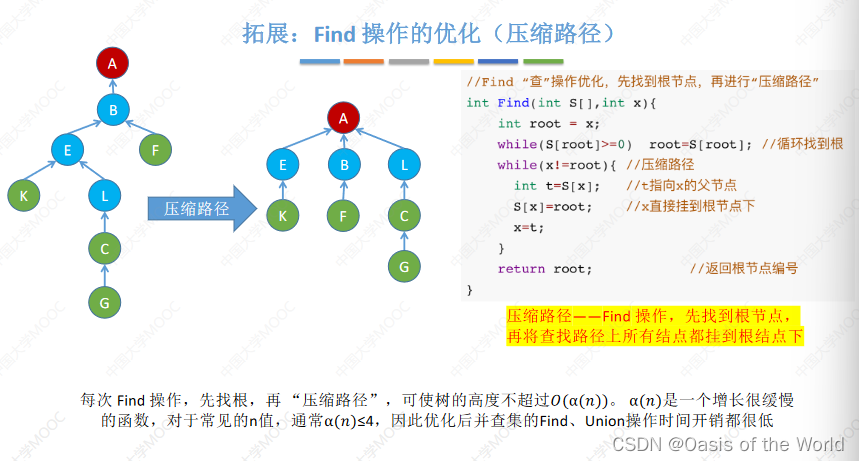
8.3 并查集的终极优化