矩阵乘法
定义与性质
矩阵乘法是线性代数中的一个基本运算,它涉及到两个矩阵的点积运算。给定两个矩阵 A(m×n)和 B(n×p),它们的乘积 C(m×p)定义为:
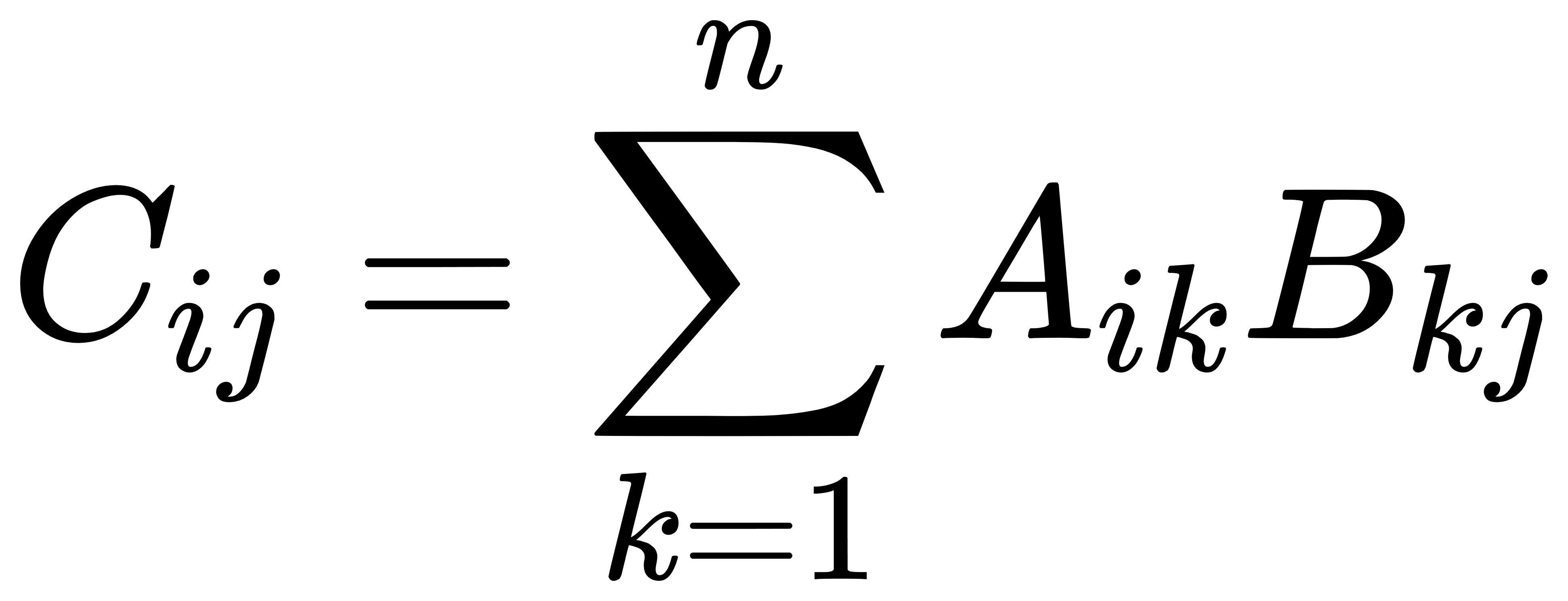
其中, Cij 是结果矩阵 C 中第 i 行第 j 列的元素, Aik 和 Bkj 分别是矩阵 A 和 B 中对应的元素。
性质
- 结合律:(AB)C=A(BC)
- 分配律:A(B+C)=AB+AC
- 不满足交换律:一般情况下 AB≠BA
应用
矩阵乘法在计算机图形学、信号处理、物理学、经济学以及工程学等多个领域都有广泛的应用。例如,在图形学中,矩阵乘法被用来实现旋转、缩放和平移等几何变换。
生活场景案例
假设你要实现一个简单的图形学中的二维旋转变换。例如,旋转一个点 (x,y) 逆时针旋转 θ 角度后的新坐标 (x′,y′) 可以通过矩阵乘法计算:
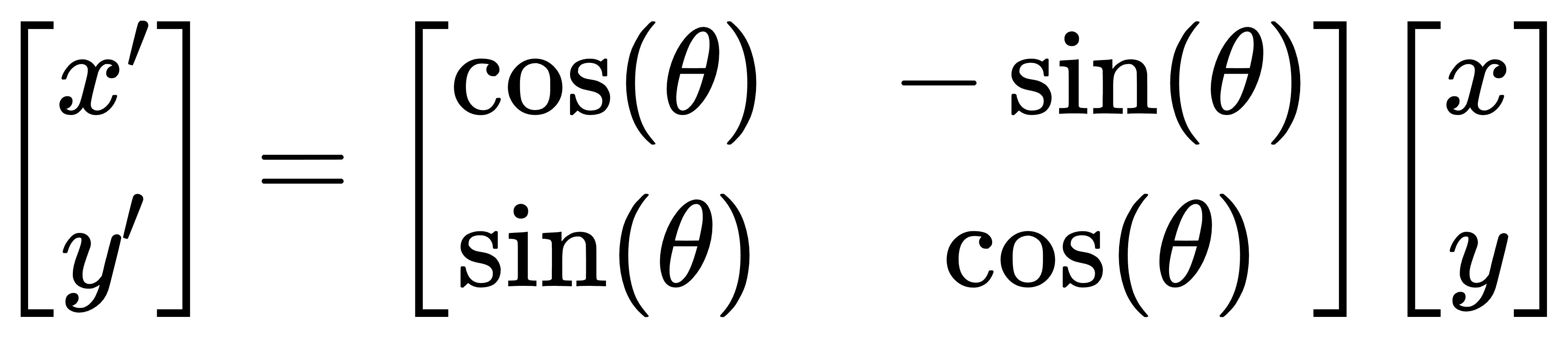
代码示例
import numpy as np
# 定义旋转矩阵
def rotation_matrix(theta):
return np.array([
[np.cos(theta), -np.sin(theta)],
[np.sin(theta), np.cos(theta)]
])
# 定义一个点 (x, y)
point = np.array([1, 0])
# 定义旋转角度(弧度)
theta = np.pi / 4 # 45度
# 计算旋转后的新坐标
rotated_point = rotation_matrix(theta).dot(point)
print("旋转后的坐标:", rotated_point)Karatsuba大数乘法
算法原理
Karatsuba算法是一种快速的大数乘法算法,由Anatolii Alexeevitch Karatsuba于1960年提出。该算法基于分治策略,通过减少乘法次数来提高效率。对于两个 n 位的数 x 和 y,Karatsuba算法可以将乘法次数从 n2 降低到大约 n1.585。
运行过程
设 x 和 y 分别为两个 n 位的数,可以将它们写作:
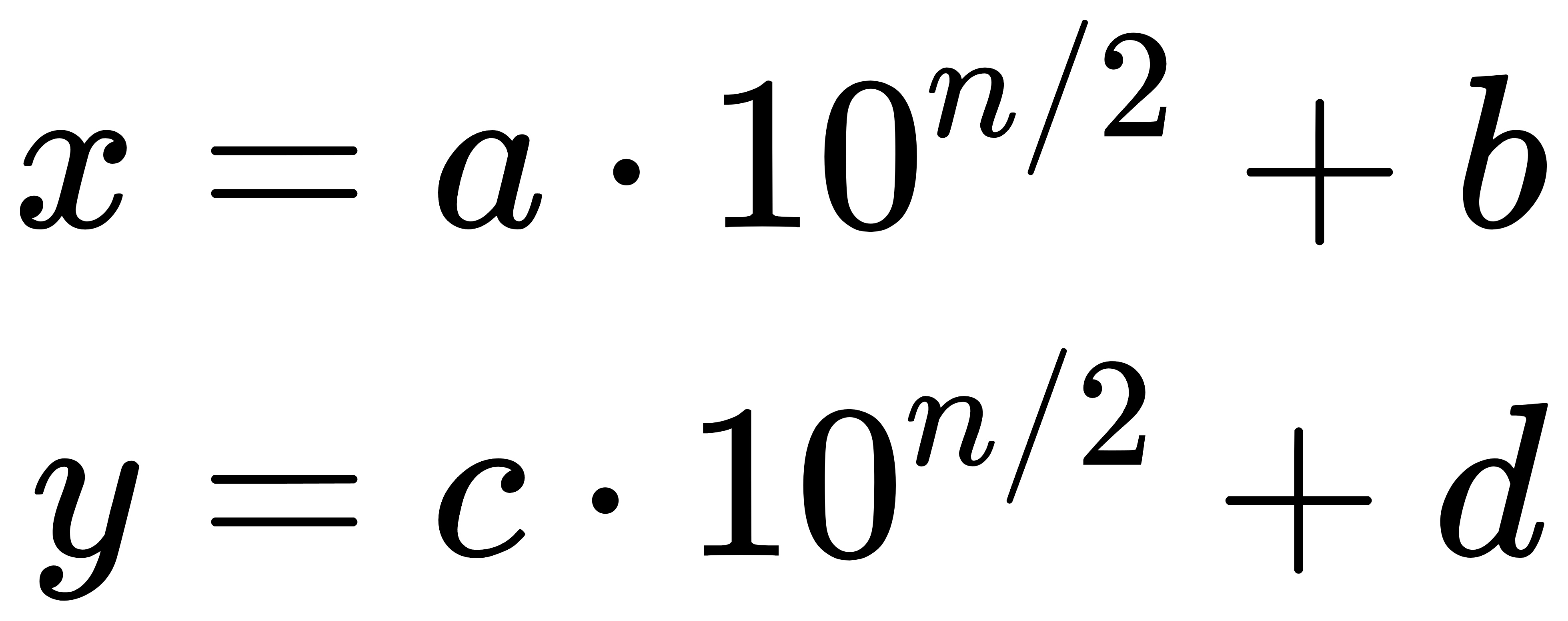
则 x × y可以表示为:
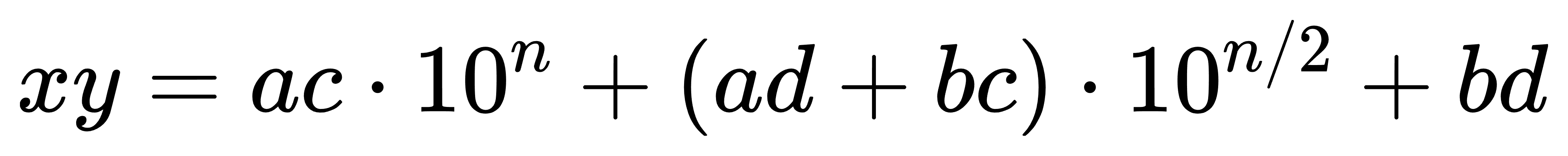
Karatsuba算法通过计算 ac、bd 以及 (a+b)(c+d),然后减去 ac 和 bd 得到 ad+bc,从而避免了直接计算 ad 和 bc。
生活场景案例
假设你需要计算两个非常大的数的乘积,例如在金融计算中需要处理非常大的数值。
代码示例
def karatsuba(x, y):
# 基础情况
if x < 10 or y < 10:
return x * y
# 计算两个数的长度
n = max(len(str(x)), len(str(y)))
m = n // 2
# 分割数字
high1, low1 = divmod(x, 10**m)
high2, low2 = divmod(y, 10**m)
# 递归计算
z0 = karatsuba(low1, low2)
z1 = karatsuba((low1 + high1), (low2 + high2))
z2 = karatsuba(high1, high2)
return (z2 * 10**(2 * m)) + ((z1 - z2 - z0) * 10**m) + z0
# 示例
x = 123456789
y = 987654321
print("Karatsuba乘积:", karatsuba(x, y))快速傅立叶变换(FFT)
原理与应用
快速傅立叶变换(FFT)是一种高效计算离散傅立叶变换(DFT)及其逆变换的算法。DFT将一个信号从时域转换到频域,而FFT则是一种能够大幅度减少计算量的算法,使得DFT在实际应用中成为可能。
计算复杂度
直接计算DFT的时间复杂度为 O(n2),而FFT的时间复杂度为 O(n·㏒n),这使得FFT在处理大规模数据集时非常高效。
实现方法
FFT的一个常见实现是Cooley-Tukey算法,它同样采用分治策略,将DFT分解为较小的DFT,然后将这些结果组合起来。这种方法依赖于复数的旋转因子,即所谓的“旋转向量”。
生活场景案例
假设你需要对一段音频信号进行频谱分析,例如音乐播放器中的频谱显示。
代码示例
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
# 设置默认字体
rcParams['font.sans-serif'] = ['SimHei'] # 使用黑体
rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 生成示例信号
Fs = 500 # 采样频率
T = 1 / Fs # 采样间隔
t = np.arange(0, 1, T) # 时间向量
# 生成包含多个频率的信号
f1 = 50 # 频率1
f2 = 120 # 频率2
signal = 3 * np.sin(2 * np.pi * f1 * t) + 1.5 * np.sin(2 * np.pi * f2 * t)
# 计算FFT
n = len(signal)
k = np.arange(n)
T = n / Fs
frq = k / T # 两侧频率向量
frq = frq[range(n // 2)] # 只取一侧
Y = np.fft.fft(signal) / n # FFT计算并归一化
Y = Y[range(n // 2)]
# 绘制信号及其频谱
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.title('信号')
plt.xlabel('时间')
plt.ylabel('幅度')
plt.subplot(2, 1, 2)
plt.plot(frq, abs(Y))
plt.title('频谱')
plt.xlabel('频率')
plt.ylabel('幅度')
plt.tight_layout()
plt.show()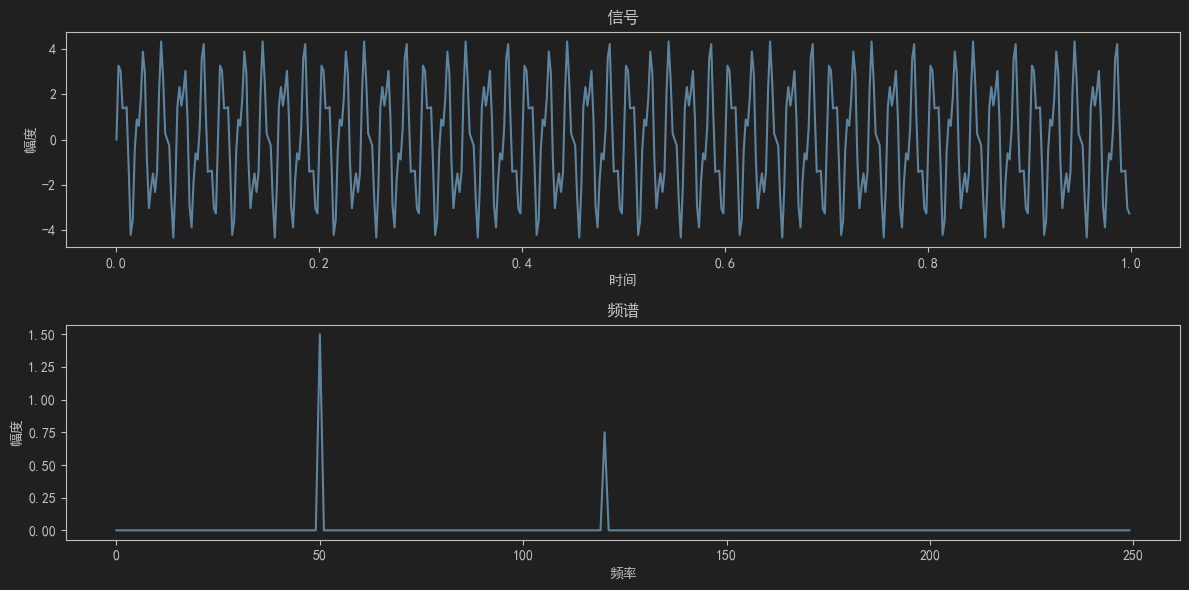


![[vue3]引入模块出现红色波浪,但是可以正常运行,去除红色波浪号](https://i-blog.csdnimg.cn/direct/2535e688edcf452bb9317abef9ff0675.png)