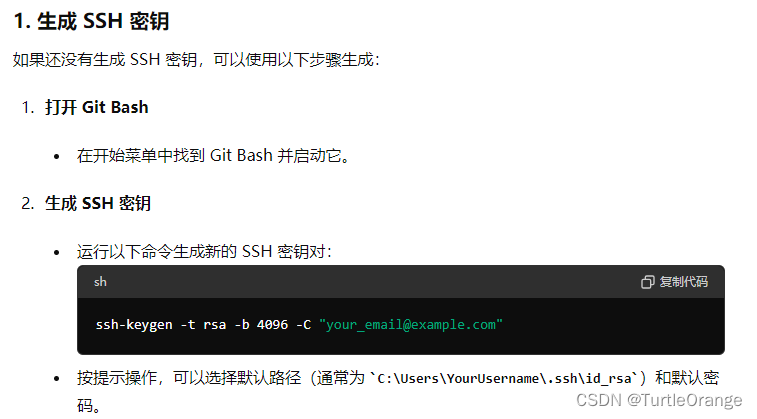
mindspore.ops模块提供的grad和value_and_grad接口可以生成网络模型的梯度。grad计算网络梯度,value_and_grad同时计算网络的正向输出和梯度。本文主要介绍如何使用grad接口的主要功能,包括一阶、二阶求导,单独对输入或网络权重求导,返回辅助变量,以及如何停止计算梯度。
一阶求导
计算一阶导数方法:mindspore.grad,其中参数使用方式为:
- fn:待求导的函数或网络。
- grad_position:指定求导输入位置的索引。若为int类型,表示对单个输入求导;若为tuple类型,表示对tuple内索引的位置求导,其中索引从0开始;若是None,表示不对输入求导,这种场景下,weights非None。默认值:0。
- weights:训练网络中需要返回梯度的网络变量。一般可通过weights = net.trainable_params()获取。默认值:None。
- has_aux:是否返回辅助参数的标志。若为True,fn输出数量必须超过一个,其中只有fn第一个输出参与求导,其他输出值将直接返回。默认值:False。
下面先构建自定义网络模型Net,再对其进行一阶求导,通过这样一个例子对grad接口的使用方式做简单介绍,即公式:
𝑓(𝑥,𝑦)=𝑥∗𝑥∗𝑦∗𝑧
首先定义网络模型Net、输入x和输入y:
import numpy as np
from mindspore import ops, Tensor
import mindspore.nn as nn
import mindspore as ms
# 定义输入x和y
x = Tensor([3.0], dtype=ms.float32)
y = Tensor([5.0], dtype=ms.float32)
class Net(nn.Cell):
def __init__(self):
super(Net, self).__init__()
self.z = ms.Parameter(ms.Tensor(np.array([1.0], np.float32)), name='z')
def construct(self, x, y):
out = x * x * y * self.z
return out
对输入求一阶导
对输入x, y进行求导,需要将grad_position设置成(0, 1):


对权重进行求导
对权重z进行求导,这里不需要对输入求导,将grad_position设置成None:


返回辅助变量
同时对输入和权重求导,其中只有第一个输出参与求导,示例代码如下:

停止计算梯度
可以使用stop_gradient来停止计算指定算子的梯度,从而消除该算子对梯度的影响。
在上面一阶求导使用的矩阵相乘网络模型的基础上,再增加一个算子out2并禁止计算其梯度,得到自定义网络Net2,然后看一下对输入的求导结果情况。
示例代码如下:

从上面的打印可以看出,由于对out2设置了stop_gradient,所以out2没有对梯度计算有任何的贡献,其输出结果与未加out2算子时一致。
下面删除out2 = stop_gradient(out2),再来看一下输出结果。示例代码为:

打印结果可以看出,把out2算子的梯度也计算进去之后,由于out2和out1算子完全相同,因此它们产生的梯度也完全相同,所以可以看到,结果中每一项的值都变为了原来的两倍(存在精度误差)。
高阶求导
高阶微分在AI支持科学计算、二阶优化等领域均有应用。如分子动力学模拟中,利用神经网络训练势能时,损失函数中需计算神经网络输出对输入的导数,则反向传播便存在损失函数对输入、权重的二阶交叉导数。
此外,AI求解微分方程(如PINNs方法)还会存在输出对输入的二阶导数。又如二阶优化中,为了能够让神经网络快速收敛,牛顿法等需计算损失函数对权重的二阶导数。
MindSpore可通过多次求导的方式支持高阶导数,下面通过几类例子展开阐述。
单输入单输出高阶导数
例如Sin算子,其公式为:
𝑓(𝑥)=𝑠𝑖𝑛(𝑥)
其一阶导数、二阶导数为:

其二阶导数(-Sin)实现如下:

从上面的打印结果可以看出,−𝑠𝑖𝑛(3.1415926)的值接近于0。
单输入多输出高阶导数
对如下公式求导:
(1)𝑓(𝑥)=(𝑓1(𝑥),𝑓2(𝑥))
其中:
(2)𝑓1(𝑥)=𝑠𝑖𝑛(𝑥)
(3)𝑓2(𝑥)=𝑐𝑜𝑠(𝑥)
梯度计算时由于MindSpore采用的是反向自动微分机制,会对输出结果求和后再对输入求导。因此其一阶导数是:
(4)𝑓′(𝑥)=𝑐𝑜𝑠(𝑥)−𝑠𝑖𝑛(𝑥)
其二阶导数为:
(5)𝑓″(𝑥)=−𝑠𝑖𝑛(𝑥)−𝑐𝑜𝑠(𝑥)

从上面的打印结果可以看出,−𝑠𝑖𝑛(3.1415926)−𝑐𝑜𝑠(3.1415926)的值接近于1。
多输入多输出高阶导数
对如下公式求导:
(1)𝑓(𝑥,𝑦)=(𝑓1(𝑥,𝑦),𝑓2(𝑥,𝑦))
其中:
(2)𝑓1(𝑥,𝑦)=𝑠𝑖𝑛(𝑥)−𝑐𝑜𝑠(𝑦)
(3)𝑓2(𝑥,𝑦)=𝑐𝑜𝑠(𝑥)−𝑠𝑖𝑛(𝑦)
梯度计算时由于MindSpore采用的是反向自动微分机制, 会对输出结果求和后再对输入求导。
求和:
(4)∑𝑜𝑢𝑡𝑝𝑢𝑡=𝑠𝑖𝑛(𝑥)+𝑐𝑜𝑠(𝑥)−𝑠𝑖𝑛(𝑦)−𝑐𝑜𝑠(𝑦)
输出和关于输入𝑥的一阶导数为:
(5)d∑𝑜𝑢𝑡𝑝𝑢𝑡d𝑥=𝑐𝑜𝑠(𝑥)−𝑠𝑖𝑛(𝑥)
输出和关于输入𝑥的二阶导数为:
(6)d∑𝑜𝑢𝑡𝑝𝑢𝑡2d2𝑥=−𝑠𝑖𝑛(𝑥)−𝑐𝑜𝑠(𝑥)
输出和关于输入𝑦的一阶导数为:
(7)d∑𝑜𝑢𝑡𝑝𝑢𝑡d𝑦=−𝑐𝑜𝑠(𝑦)+𝑠𝑖𝑛(𝑦)
输出和关于输入𝑦的二阶导数为:
(8)d∑𝑜𝑢𝑡𝑝𝑢𝑡2d2𝑦=𝑠𝑖𝑛(𝑦)+𝑐𝑜𝑠(𝑦)