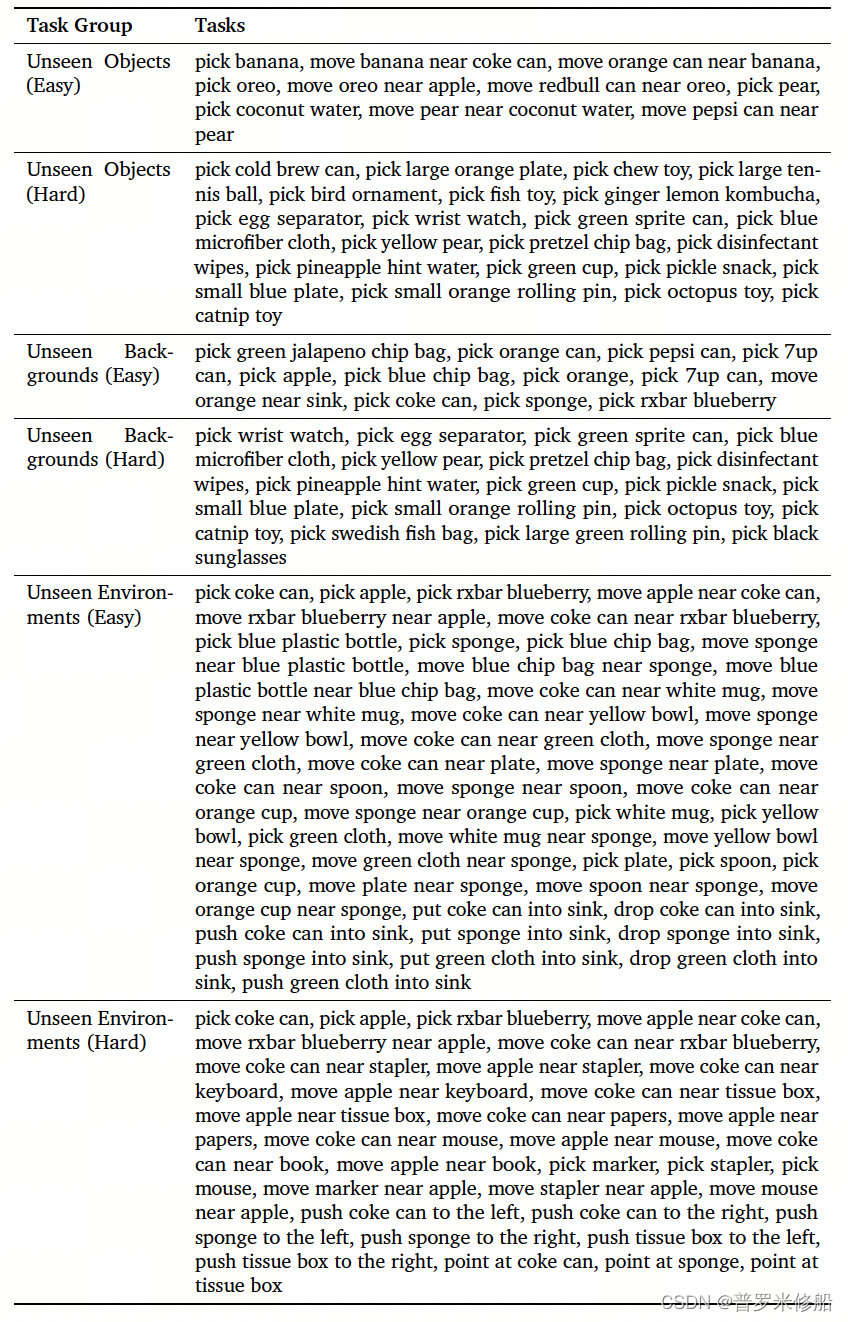
(内容源自详解MATLAB/SIMULINK 通信系统建模与仿真 刘学勇编著第六章内容,有兴趣的读者请阅读原书)




clear all
Fd=1;%符号采样频率
Fs=10;%滤波器采样频率
r=0.2;%滤波器滚降系数
delay=4;%滤波器时延
[num,den]=rcosine(Fd,Fs,'default',r,delay);%设计滤波器
figure;impz(num,1);%滤波器的冲激响应(1)
title('滤波器的冲激响应')
x=randi([0,1],1,30);%二进制数据序列
[y,ty]=rcosflt(x,Fd,Fs,'filter',num,den);%用已经设计好的滤波器对输入数据进行滤波,即对二进制数据进行脉冲成形
%其中y是滤波的结果,ty是出现对应结果的时间
figure
t=delay:length(x)+delay-1;
stem(t,x,'-r');hold on%画出二进制数据
plot(ty,y)%画出脉冲成形的数据
legend('二进制数据','脉冲成形后的数据')
axis([-1 40 -0.5 2])(1)关于函数impz的使用,详见
http://t.csdnimg.cn/Vk7lz
在此可以简述为:在此次滤波过程中分母系数为1,分子系数为num。


clear all
nsymbol=100000; %每种信噪比下的发送符号数
Fd=1;%符号采样频率
Fs=10;%滤波器采样频率
rolloff=0.25;%滤波器滚降系数
delay=5;%滤波器时延
M=4;%4-PAM
graycode=[0 1 3 2];%格雷编码准则
EsN0=0:15;%信噪比,E/N0
msg=randi([0,3],1,nsymbol);%消息数据
msg1=graycode(msg+1);%格雷映射
msgmod=pammod(msg1,M);%4-PAM调制
rrcfilter=rcosine(Fd,Fs,'fir/sqrt',rolloff,delay);%设计根升余弦滤波器
s=rcosflt(msgmod,Fd,Fs,'filter',rrcfilter);%通过根升余弦滤波器进行脉冲成形
for indx=1:length(EsN0)
decmsg=zeros(1,nsymbol);
r=awgn(real(s),EsN0(indx)-7,'measured');%通过AWGN信道
rx=rcosflt(r,Fd,Fs,'Fs/filter',rrcfilter);%通过根升余弦滤波器进行相关
rx1=downsample(rx,Fs);%相关器采样
rx2=rx1(2*delay+1:end-2*delay);%去掉延迟
msg_demod=pamdemod(rx2,M);%判决
decmsg=graycode(msg_demod+1);%格雷逆映射(1)
[err,ber(indx)]=biterr(msg,decmsg,log2(M));%求误比特率
[err,ser(indx)]=symerr(msg,decmsg);%求误符号率
end
semilogy(EsN0,ber,'-ko',EsN0,ser,'-k*',EsN0,1.5*qfunc(sqrt(0.4*10.^(EsN0/10))));%(2)
title('4-PAM信号在AWGN理想带限信道下的性能')
xlabel('Es/N0');ylabel('误比特率和误符号率')
legend('误比特率','误符号率','理论误符号率')(1)因为调制信号在发送端和接收段均使用根升余弦滤波器进行滤波,所以一共要使用根升余弦滤波器进行两次相关,总体思路如下
(发送端)消息数据-》格雷码映射-》4-PAM调制-》通过滤波器进行脉冲成形-》通过AWGN信道-》
(进入接收端)-》再次通过滤波器进行脉冲成形-》相关器采样(脉冲成形的逆过程)-》去延迟(滤波器自身含有延迟)-》判决(4-PAM的逆过程)-》格雷逆映射-》消息数据
(2)理论的误符号率是通过式6-25推出来的