计算的时间问题！计算机解决了计算量的问题！

计算机的发展对运筹学研究起到了极大的促进作用。

运筹学的一个特征之一是它常常会考虑寻求问题模型的最佳解决方案（称为最优解）。

没有人能成为运筹学所有方面的专家。

分析学越来越流行，主要是因为我们进入了大数据时代，许多企业和组织可以获得大量数据（伴随着大量的计算能力），以帮助指导管理决策。分析学的一个重点事如何最有效地利用这些数据。

分析学与运筹学之间的密切合作将会继续加深。

运筹学能够提升组织效率和生产率。

通用汽车是全世界最早使用分析学和运筹学的用户之一。

运筹学/管理科学技术被用于提高我们对每件事情的理解，从交通科学和供应链物流到制造生产力、产品开发、车辆远程信息处理和预测。这些问题的解决方法几乎渗透到我们做的每件事中。

运筹学分析师的就业需求会增长。

LINGO仍然是受欢迎的运筹学软件包。

运筹学团队通常扮演顾问的角色。

对于盈利组织，避免局部最优化的可行方法是将长期收益最大化作为唯一的目标。

信用评分公司：数据挖掘。

使用规范性模型和优化模型来改进管理层的决策。

原子模型、物理公式，这些模型在抽象问题本质、表明相互关心及促进分析等方面的价值是无法估量的。

大陆航空公司在运用运筹学中的数学模型，一年节约了近4000万美金。

求解线性规划问题--单纯形法

对偶理论

对偶关系：一个问题第i个变量的约束情况决定另一个问题第i个约束不等式的方向，反之亦然。

正常的对正常的，不正常的对不正常的。

定理1(弱对偶定理)：

极大化原问题目标函数值总是不大于其对偶问题的目标函数值。

推论1：

若LP问题有无界解，则其对偶问题无可行解；

若LP问题无可行解，则对偶问题或有无界解或无可行解。

推论2：

极大化问题的任何一个可行解所对应的目标函数值都是其对偶问题目标函数值的下界。

推论3：

极小化问题的任何一个可行解所对应的目标函数都是其对偶问题目标函数值的上界。

定理2（最优化准则）：当LP问题目标函数值与其对偶问题目标函数值相等时，各自的可行解即为最优解。

定理3（强对偶定理）：若（L），（D）均有可行解，则（L），（D）均有最优解，且目标函数最优值相等。

推论：

在用单纯形法求解LP问题（L）的最优单纯形表中，松弛变量的检验数的相反数就是其对偶问题（D）的最优解。

定理4（互补松弛定理）：在最优情况下，原问题的第i个决策变量与其对偶问题第i个约束中的松弛变量的乘积恒为零。

不确定情况下的线性规划

线性规划的其他算法

运输和指派问题

网络优化模型

一笔画定理：连通图中，与偶数条线相连的点叫偶点，与奇数条线相连的点叫奇点，奇点的个数超过2个的图不能一笔画出。

边：两点之间不带箭头的联线。记为e=[v1,v2]。

无向图：记为G=（V,E），V，E分别是G的点集合与边集合。

有向图：记为D=（V,A），V，A分别是D的点集合与弧集合。

弧：两点之间带箭头的联线。记为a=(v1,v4)。

环：

多重边：

简单图：一个无环、无多重边的图。

多重图：

点的次：以v为端点的边的个数。

悬挂点：次为1的点

悬挂边：悬挂点的关联边

孤立点：

偶点：

奇点：

链：

中间点：

初等连：

圈：

初等圈：

简单圈，简单链：

连通图：

连通分图：

图G或D中点的个数：p(G) p(D)。

图G或D中边的个数：q(G) q(D)。

支撑子图：

基础图：

路

初等路：

回路：

简单有向图：

多重有向图：

定理1 设图G=(V,E)是一个树，p(G)>=2，则G中至少有两个悬挂点。

定理2 图G=(V,E)是一个树的充分必要条件是G中不含圈，且恰有p-1条边。

定理3 图G=(V,E)是一个树的充分必要条件是G是连通图，并且q(G)=p(G)-1。

定理4 图G是树的充分必要条件是任意两个顶点之间恰有一条链。

推论：从一个树中去掉一条边，则余下的图是不联通的。在树中不相邻的两点间添上一条边，则恰好得到一个圈。

设图T=(V,E)是图G的支撑子树，如果图T=(V,E')是一个树，则称T是G的一个支撑树。

图G有支撑树的充分必要条件是图G是联通的。

最小支撑树：

避圈法（最小支撑树的求法）：

开始选一条权最小的边，以后每一步中，总从未被选取的边中选一条权最小的边，并使之与已选的边不构成圈。

破圈法：任取一个圈，从圈中去掉一条权最大的边。在余下的图中，重复这个步骤，直到得到不含圈的图为止，这时的图便是最小树。

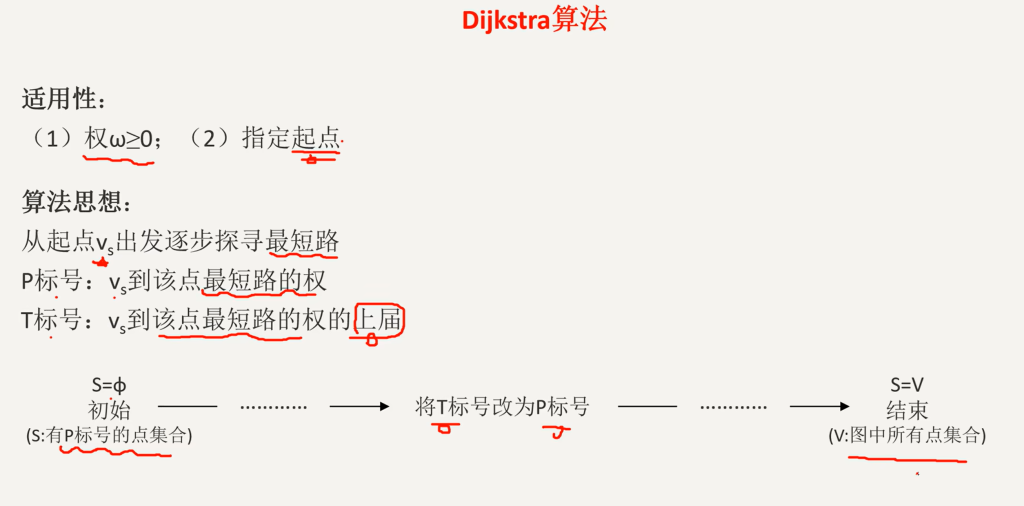
狄克斯特拉算法

所有的权均为非负。

寻找起点已标号而终点未标号的最小值。

狄克斯特拉算法

优点：

能找到从起点到所有点的最短路。

缺点：

不能解决带有负权的图的最短路问题。

最小费用最大流问题：

伴随网络流f的增流网络：

无圈的连通图

有向图的Dijkstra算法：

权：实际是费用，时间等

T标号都是临时的，

网络最大流：

权 - > 流量

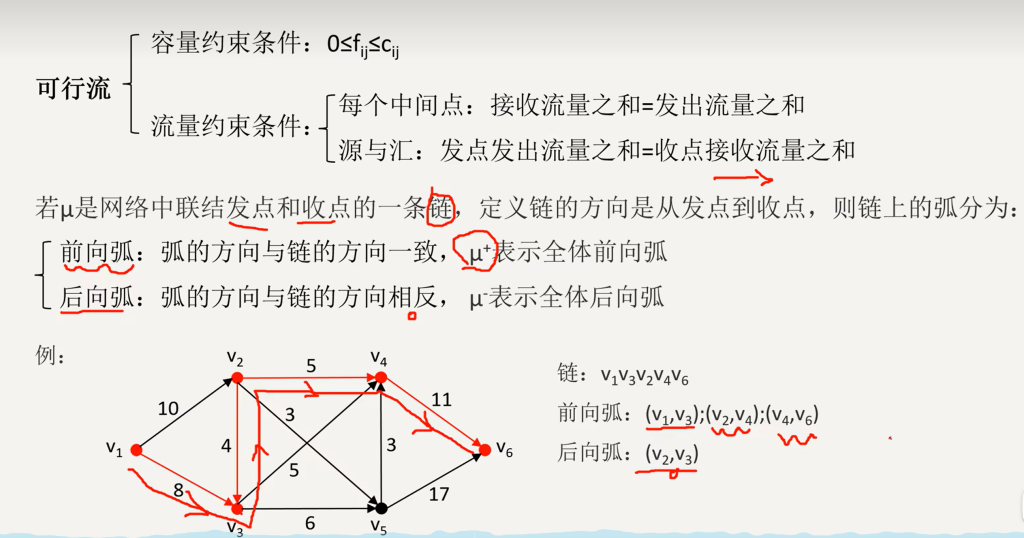
后向弧：

前向弧：

割集（截量）：

最小割集的弧是饱和弧！

割量（截量）：

可行流：

增广链：

最大可行流：

正向弧 --- 流量小于容量：可以标号

饱和弧不能标号！！！

后向弧：能否标号，后向弧的流量大于0！！！

后向弧的标号，标的是流量！！！

双箭头：增广链！！！

前序节点

c:费用 f:流量 b:容量

同向的弧代表流量可以增加，反向的弧代表流量可以减少！

c:容量 b:费用

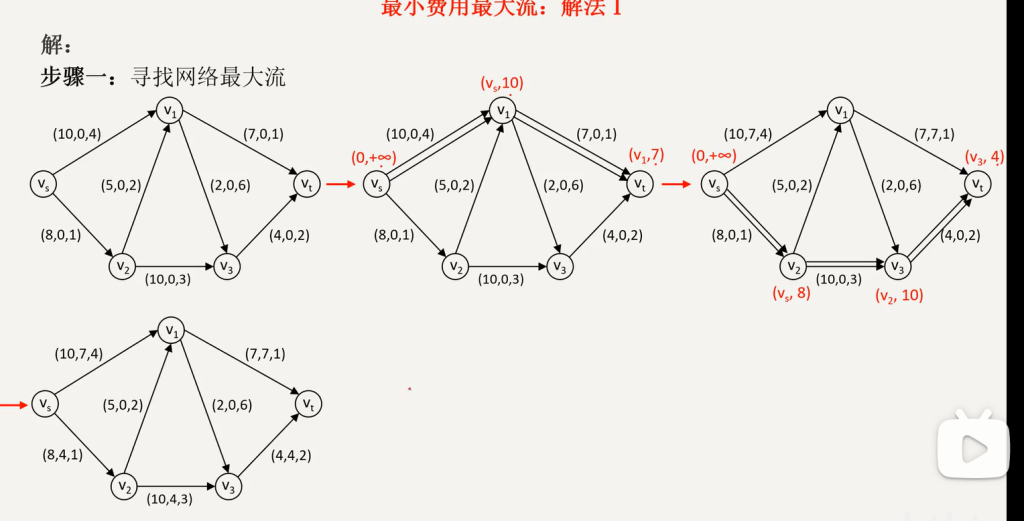
调整流量！！！

增大流量！！！

无语的一天，下大雨了，下午到晚上困的要死！

动态规划

整数线性规划

指派问题

决策分析

排队论