蓝桥杯-长草

news2024/11/20 4:36:10

没有白走的路，每一步都算数🎈🎈🎈

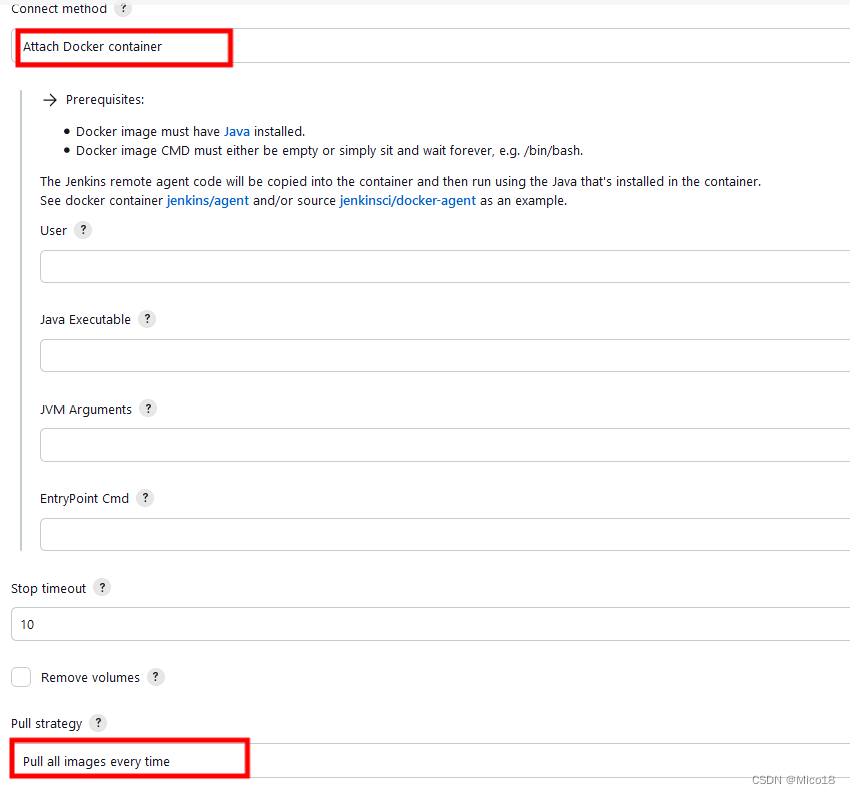
题目描述：

已知一个长度为n，宽度为m的长方形草地，但不是每一个方格里面都长满了草，只有部分的方格张了些草。并且每个月草会向上下左右都繁殖一个草，并且满足在边界范围内。即若衍生的草不在边界范围内的，就不会生长。试求第k个月之后，这块方形地的生长情况是怎么样的？

输入描述：

第一行：

输入两个数据，n,m分别表示长方形地区的长度和宽度

第二行及其n行：

每行m个数据，表示第n行的长草情况，其中该块地若长草，我们用g表示，否则用.表示。

最后一行，输入k表示，这块地生长了多少个月

输出描述：

输出k个月之后，这块土地的草地情况

样例输入输出：

样例输入:

4 5

.g...

.....

..g..

.....

样例输出：

gggg.

ggggg

.ggg.

算法分析：

显然这是一道BFS的题目。此次用时4个多小时，写出了超时的代码，部分样例没有通过。

数据结构定义：

mp数组：表示杂草地，g表示杂草，.表示空地
d数组：表示递归桥梁的数组
a数组：存放第一次BFS位置，即输入数据中g的位置

代码设计：

最开始的分割字符，map(str,input())非常适合用于分割很多连在一起的数据 ps:这里卡住一段时间
bfs函数，这里卡住最长时间，当初bfs（）函数传参的时候，没有把k写入进去，出现bug。导致，对样例的k=2时，出现有部分杂草没有繁殖。遂改成三个参数的情况。
逻辑有点小错误

这里不应该写成if mp[ni][nj]=='.':，直接删除即可，因为这样会误导至有些杂草也不会繁殖。

最后就是解决超时问题。

#长草
import os
import sys
n,m = map(int,input().split())
mp = [list(map(str,input()))for i in range(n)]
k = int(input())
d = [[0,1],[0,-1],[1,0],[-1,0]]
a = []

def bfs(i,j,k):
    if k<=0:
        return 
    for x in range(4):
        ni,nj = i+d[x][0],j+d[x][1]
        if 0<=ni<=n-1 and 0<=nj<=m-1:
            mp[ni][nj] = 'g'
            bfs(ni,nj,k-1)

for i in range(n):
    for j in range(m):
        if mp[i][j] =='g':
            a.append([i,j])
for x in a:
    bfs(x[0],x[1],k)

for i in range(n):
    for j in range(m):
        print(mp[i][j],end = '')
    print()

改进版BFS:

数据结构：

导入deque包，BFS几乎都会用到这个，以及常用popleft方法

from collections import deque
n,m = map(int,input().split())
mp = [list(map(str,input()))for i in range(n)]
##print(mp)
k = int(input())
q = deque()
for i in range(n):
    for j in range(m):
        if mp[i][j] == 'g':
            q.append((i,j,k))

##print(q)
while True:
    x,y,z = q.popleft()
    if z==0:
        for i in range(n):
            print(''.join(mp[i]))
        break
    for i,j in [[1,0],[-1,0],[0,1],[0,-1]]:
        nx,ny = x+i,y+j
        if 0<=nx<n and 0<=ny<m and mp[nx][ny]=='.':
            mp[nx][ny]='g'
            q.append((nx,ny,z-1))