Value funtion methods-为什么我们用回了Q函数？

先回顾一下在AC中的基于V函数的框架：

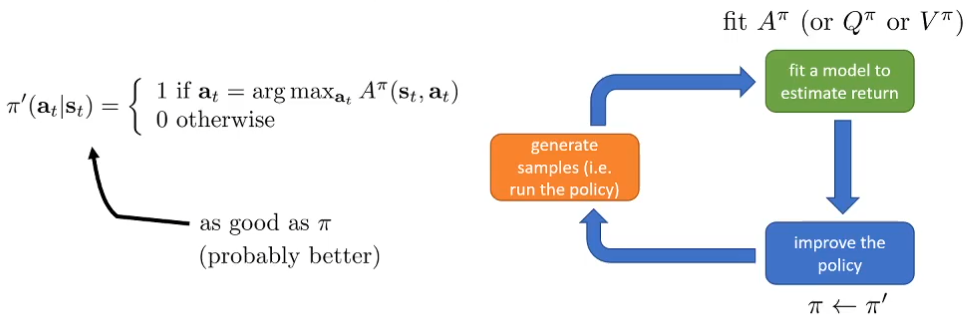
另一个想法：不依赖梯度，而是直接根据值函数去决定动作：V函数已经告诉了我们哪些状态更好

[!NOTE] 思路：
$A^{\pi }(s_t,a_t)$意义是动作$a_t$比根据策略$\pi$产生的平均动作reward好多少：Advantage
$\arg {\max }_{a_t}{A}^{\pi }(s_t,a_t)$表示从状态$s_t$出发，按照策略$\pi$能够采取的最好的动作——我们可以忘掉显式的策略，只用价值去决定动作（想想AC中，我们还有一个神经网络去专门拟合S到a的策略，输出a的分布）
因此，不管策略有多差，总是能够不断选择改善的，这就是Value function methods的基础

Q-iteration

一个简单的Q-Learning，其实在背后的数学来历如此的深刻。——7.11
根据上面的更新规则，实际上$\pi (s)=a$是一个固定的策略：总是选择最大收益的动作，因此，V函数可以被简化：
$$V^{\pi }(s)\leftarrow r(s,\pi (s))+\gamma E_{s^{\prime }\sim P(s^{\prime }|s,\pi (s))}[V^{\pi }(s^{\prime })]$$
在实际代码中，就是一个存储$V^{\pi }(s)$的表格，不断迭代，整个过程不需要显式的策略

因为$\arg {\max }_{a_t}{A}^{\pi }(s_t,a_t)$是寻找最大值的$a_t$，而$A^{\pi }(s,a)$:
$$A^{\pi }(s,a)=r(s,a)+\gamma E[V^{\pi }(s^{\prime })]-V^{\pi }(s)$$
最后一项和a没关系，可以删掉，而删掉之后，就是Q的定义：$Q^{\pi }(s,a)=r(s,a)+\gamma E[V^{\pi }(s^{\prime })]$
因此我们利用新的Q表格与更新方法：

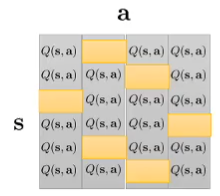
每次寻找每一行的最大值对应的a，其实也就是$\arg {\max }_{a_t}{A}^{\pi }(s,a)$作为动作，而这个最大值就是V函数。V函数的期望又可以用Q函数的最值来近似，下面是Q迭代的方法：

1. set $Q(s,a)\leftarrow r(s,a)+\gamma E[V(s^{\prime })]$
2. set $V(s)\leftarrow {\max }_{a}Q(s,a)$

[!NOTE] Q-table -> Q-iteration
由于我们这里还是用的Q表格，因此$E[V(s^{\prime })]$是比较好得到的——对应离散空间
但是，离散的空间维度是$s\times s\times a$，有可能变得非常大，尤其在输入是图像时，因此我们需要借助神经网络去实现策略的更新！
这就是下面这一部分要做的事情（复盘时突然明白了）

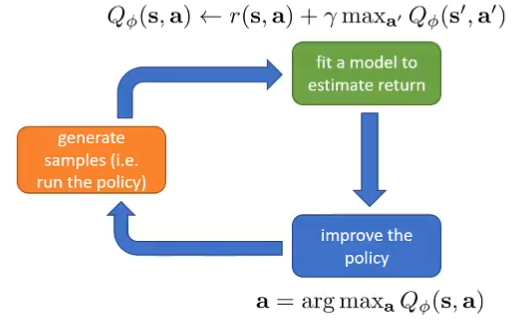
试图用神经网络去fit，将会得到：

Q-Learning (P30)

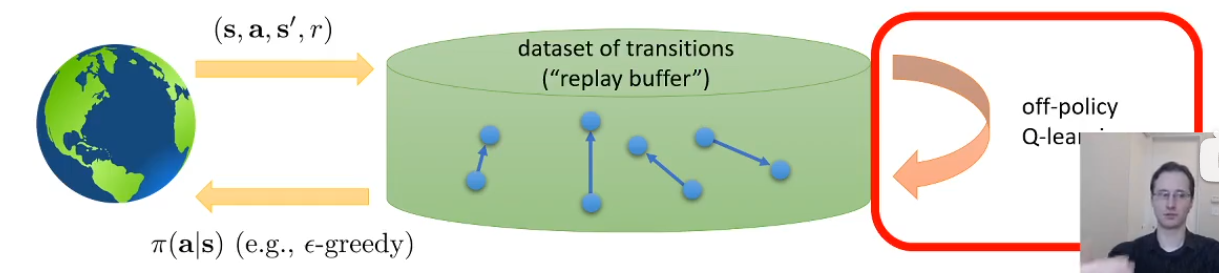
off-policy：Q-iteration不需要从最新的策略去采样，即模型梯度下降了之后仍任可以用之前的数据去训练。成批次的进行采样和训练

on-policy：Q-Learning
因为没法像off-policy一样一次收集多个数据集，在第三步做一个求和，因此才要换一种梯度更新，但是这并不等同于梯度下降，因为不是求目标的梯度
这一块可以多多讲述off和on的区别，还有包括数据集采样的不同和policy的不同

[!探索]
上面off-policy算法中的第一步“用某种策略去执行动作收集数据集”，是指更新策略并去实际环境中运行，收集一些数据集。而更新策略可以用不同的探索方法
我们需要再原本的on-policy基础上改变一下$\pi (a_t|s_t)$的更新规则，因为总是选择最好的策略不一定最后最好

1. $\pi (a_t|s_t)=1-ϵif{a}_t=\arg {\max }_{a_t}{Q}_{\varphi }(s_t,a_t)$，有$ϵ$的概率去选择别的action
2. $\pi (a_t|s_t)\propto \exp (Q_{\varphi }(s_t,a_t))$ Boltzmann exploration，优点：已经知道某个action很差，那么大概率不会选它，如果有两个action的value都很高，那么选择他们的概率比较接近。
   整个Q-Learning是不需要具体的policy的，policy被隐式的包含在${\max }_{a}Q$里面了，但是我们可以通过价值函数去恢复policy