力扣第二十五题——K个一组反转链表

news2024/11/25 13:30:42

内容介绍

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：
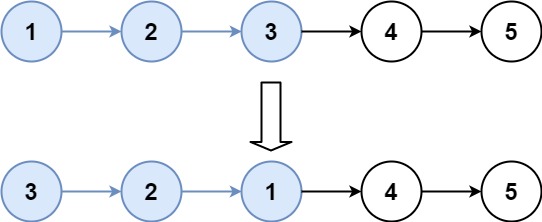
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]
示例 2：
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]
提示：
链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

完整代码

 class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode hair = new ListNode(0);
        hair.next = head;
        ListNode pre = hair;

        while (head != null) {
            ListNode tail = pre;
            // 查看剩余部分长度是否大于等于 k
            for (int i = 0; i < k; ++i) {
                tail = tail.next;
                if (tail == null) {
                    return hair.next;
                }
            }
            ListNode nex = tail.next;
            ListNode[] reverse = myReverse(head, tail);
            head = reverse[0];
            tail = reverse[1];
            // 把子链表重新接回原链表
            pre.next = head;
            tail.next = nex;
            pre = tail;
            head = tail.next;
        }

        return hair.next;
    }

    public ListNode[] myReverse(ListNode head, ListNode tail) {
        ListNode prev = tail.next;
        ListNode p = head;
        while (prev != tail) {
            ListNode nex = p.next;
            p.next = prev;
            prev = p;
            p = nex;
        }
        return new ListNode[]{tail, head};
    }
}

思路详解

一、解决思路

辅助头节点：创建一个辅助头节点hair，其下一个节点指向原链表的头节点head。这样做的好处是在翻转链表的过程中，可以简化边界条件的处理。
分组检查：使用一个循环来检查链表中剩余的节点是否至少有 k 个，以决定是否进行翻转。
翻转链表：对于每一组 k 个节点，使用一个辅助函数myReverse来进行翻转。
重新连接：翻转后，需要将翻转的子链表重新连接到原链表中。

二、详细步骤

初始化辅助头节点：
```
ListNode hair = new ListNode(0);
hair.next = head;
ListNode pre = hair;
```
这里pre节点用于在翻转后重新连接链表。
遍历链表：
```
while (head != null) {
```
当head不为空时，继续处理链表。
检查剩余节点数量：
```
ListNode tail = pre;
for (int i = 0; i < k; ++i) {
    tail = tail.next;
    if (tail == null) {
        return hair.next;
    }
}
```
通过一个循环，检查从当前pre节点开始的 k 个节点是否存在。如果不足 k 个，则直接返回辅助头节点的下一个节点。
记录翻转后的子链表：
```
ListNode nex = tail.next;
ListNode[] reverse = myReverse(head, tail);
head = reverse[0];
tail = reverse[1];
```
myReverse函数翻转从head到tail的子链表，并返回翻转后的头尾节点。
重新连接链表：
```
pre.next = head;
tail.next = nex;
pre = tail;
head = tail.next;
```
将翻转后的子链表连接回原链表，并更新pre和head指针。

翻转函数：

public ListNode[] myReverse(ListNode head, ListNode tail) {
    ListNode prev = tail.next;
    ListNode p = head;
    while (prev != tail) {
        ListNode nex = p.next;
        p.next = prev;
        prev = p;
        p = nex;
    }
    return new ListNode[]{tail, head};
}

该函数通过迭代的方式翻转链表，直到p指向tail。

四、返回结果